Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2. ОБЩАЯ ТЕОРИЯ ТУРБОМАШИН
Рабочий орган радиальной (центробежной) машины представляет собой круговую решетку, а у осевой машины – прямолинейную решетку, непрерывно обтекаемую текучим потоком.
С целью выяснения закономерности процесса их взаимодействия с потоком первоначально изучим его на отдельном изолированном крыле (лопасти), когда оно обтекается безвихревым плоско-параллельным потоком, удаленным на достаточно большом расстоянии от крыла.
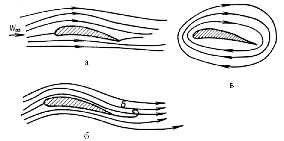
При набегании потока на крыло, расположенное под некоторым углом α к направлению скорости текучего, происходит раздваивание потока и в первый момент движение за крылом имеет вид, показанный на рис. 2.1, а. Затем за ним образуется вихрь Б (рис. 2.1, б), отделяющийся от крыла [5].
|
|
|
Рис. 2.1. Картина обтекания профиля потоком: |
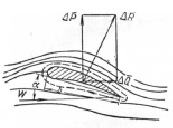
Вследствие вышеуказанного явления вокруг крыла возникает круговое движение (рис. 2.1, в), накладывающееся на основной поток. Поэтому на верхней стороне крыла происходит совпадение течений и скорость потока увеличивается, в то время как на нижней стороне направление течений оказывается встречным и суммарная скорость обтекания уменьшается. Благодаря этому давление потока с нижней стороны лопасти оказывается больше, чем в верхней, и возникает подъемная сила крыла ∆Р, направленная перпендикулярно скорости текучего W (рис. 2.2).
Вследствие вязкости потока текучее стекает по касательной к крылу и несколько отклоняет поток от первоначального направления, одновременно стремясь сдвинуть крыло вместе с потоком, что обусловливает появление силы сопротивления ∆Q.
Таким образом, на крыло постоянно и одновременно действует результирующее усилие ∆R (рис. 2.2), равное геометрической сумме сил ∆Р и ∆Q [5].
|
|
|
Рис. 2.2. Схема распределения усилий, действующих на крыло |
Теоретическую величину подъемной силы крыла ∆Р впервые определил проф. Н. Е. Жуковский:
∆P=ρ·W·∆l·Г, (2.1)
где ρ – плотность текучего, кг/м3; W – скорость невозмущенного потока, или скорость перемещения тела в потоке, м/с; ∆l – длина элемента лопасти; Г – циркуляция скорости вокруг лопасти, характеризующая интенсивность кругового потока вокруг крыла, м2/с.
Величина циркуляции Г определяется также по формуле Жуковского:
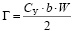 , (2.2)
, (2.2)
где СУ – коэффициент подъемной силы; числовое значение его зависит от угла α (угол, заключенный между хордой профиля и направлением скорости) и размаха крыла b/Δl; b – хорда профиля.
После подстановки значения Г в формулу (2.1) получаем подъемную силу крыла
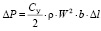 , (2.3)
, (2.3)
Основной причиной появления подъемной силы является вязкость текучего, и если она равна нулю, то и ∆Р равна нулю.
Из уравнения следует, что если при движении тела в потоке или, наоборот, при движении потока вдоль лопасти не образуется циркуляция, то подъемная сила также равна нулю и передача энергии от лопасти к текучему невозможна. Поэтому движение крыла в реальном текучем всегда обусловлено возникновением циркуляционного течения вокруг лопасти, приводящего к созданию повышенного давления на набегающей стороне лопасти и пониженного давления на ее противоположной стороне.
Одновременно с подъемной силой ∆Р (вследствие вязкости среды) возникает сила лобового сопротивления крыла ∆Q, определяемая по уравнению
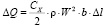 , (2.4)
, (2.4)
где СX – коэффициент лобового сопротивления, зависящий от тех же факторов, что и СУ.
Отношение коэффициента СУ к СX называется качеством профиля лопасти и показывает, во сколько раз подъемная сила больше силы лобового сопротивления.
До сих пор все приведенные закономерности относились к взаимодействию одной лопасти с потоком, в случае перемещения решетки лопастей в потоке жидкости происходит искривление последнего и за решеткой поток приобретает иное направление, чем до решетки.
Для определения подъемной силы решетки, как это показал Чаплыгин, необходимо вместо скорости невозмущенного потока подставлять величину скорости WТ, равную геометрической полусумме скоростей потока перед и за решеткой.
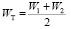 . (2.5)
. (2.5)
Направление подъемной силы, как и для одиночной лопасти, остается перпендикулярным к скорости WТ и направлено в сторону, противоположную циркуляции вокруг лопасти.
Вихрем называется движение частиц жидкости в пространстве вокруг некоторой мгновенной, неподвижной или перемещающейся оси подобно твердому телу.
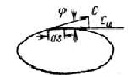
В любой вязкой среде вокруг вихря образуется поле скоростей, интенсивность которого измеряется циркуляцией Г, последняя равна
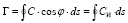 , (2.6)
, (2.6)
где С – скорость жидкости в данной точке контура; СИ – проекция скорости на касательную контура в данной точке; ds – элемент длины контура; φ – угол между направлением скорости С и элементом ds.
Таким образом, циркуляция – это кинематическая характеристика течения жидкости, представляет собой работу вектора скорости по контуру.
В частном случае, когда во всех точках контура скорость одинакова и направлена по касательной к нему, а сам контур представляет собой окружность радиуса R, циркуляция вычисляется по формуле:
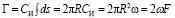 , (2.7)
, (2.7)
Следовательно, циркуляция или напряжение вихря по некоторому контуру, где вихрь не меняется, равна удвоенному произведению площади вихря на его угловую скорость, что имеет место при вращении рабочего колеса.
За положительное значение циркуляции принято считать движение по контуру в направлении часовой стрелки, а за отрицательное – при обходе контура против часовой стрелки (рис. 2.3).
|
|
|
|
Рис. 2.3. Схема циркуляции |
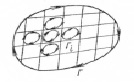
Рис. 2.4. Схема суммирования |
Для определения циркуляции по какому-то контуру разобьем его внутреннюю поверхность на бесконечное множество элементарных площадок и изобразим циркуляцию в каждой из них в виде вихря, вращающегося по часовой стрелке. При определении суммы всех циркуляций замечаем, что по линиям, разграничивающим смежные площади, циркуляции взаимно исключаются, так как они равны по величине и противоположны по направлению (рис. 2.4).
Таким образом, останется лишь внешняя циркуляция, равная сумме циркуляций внутри контура
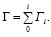 (2.8)
(2.8)
Если контур не охватывает вихрь, то циркуляция скорости вокруг него равна нулю [5].