Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

5.4. Моделирование термоокислительной деструкции с помощью дерева Кейли

В настоящее время предполагается [53], что термоокислительная деструкция полиэтиленов может протекать в двух режимах: кинетическом и диффузионном. При этом деструкция тонких (< 1мм) образцов протекает в кинетическом, а массивных (> 1 мм) - в диффузионном режиме. Отметим, что уже приближенный критерий, определяющий границу двух указанных режимов, указывает на эмпирический и условный характер классификации режимов, тем более, что физические и химические процессы, протекающие при термоокислительной деструкции, в обоих режимах полностью идентичны - диффузия молекул кислорода в материал и их реакция с реакционноспособными центрами молекул полиэтилена. Тем не менее, как показали экспериментальные наблюдения, периоды индукции для одного и того же полиэтилена при одинаковых условиях теплового старения различаются для двух указанных режимов примерно на порядок. Авторы работ [54; 55] выполнили анализ указанного различия величин   в рамках как классических, так и фрактальных моделей на примере ПЭВП.

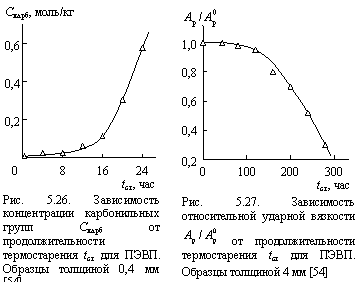
Как показали экспериментальные исследования теплового старения пленочных и массивных образцов ПЭВП [26; 56], продолжительность периода индукции , в течение которого полиэтилен сохраняет допустимый уровень эксплуатационных показателей, различается для указанных типов образцов примерно на порядок и составляет ~ 10 час. для пленок и ~ 100 час. для массивных образцов при Т_ст = 353 К (рис. 5.26 и 5.27, см. также рис. 5.6).

Рассмотрим возможные причины этого различия. В рамках классических подходов можно рассматривать вариацию   как следствие изменения t_d - времени, в течение которого диффузионный фронт достигает медианной плоскости образца (предполагается, что этот фронт движется от обеих сторон образца к медианной плоскости одновременно). В этом случае величина t_d должна быть примерно равна t_ин. Определить t_d можно из хорошо известного уравнения [57]:

,                                                         (5.23)

где l - половина толщины образца, - коэффициент диффузии ПЭВП по кислороду.

Величину   для ПЭВП при Т = 353 К можно принять по данным работы [58] равной 6,31 ´ 10^-9 м²/с. Тогда расчет по уравнению (5.23) дает величины t_d порядка 2 мин для массивных образцов и порядка 1с - для пленок. Даже с учетом того факта, что стационарный поток газа через полимер устанавливается за промежуток времени, в три раза превышающий t_d, указанные величины t_d не объясняют экспериментально наблюдаемых величин .

Авторы [54; 55] объяснили такое различие величин t_d и  в рамках модели аномальной диффузии на фракталах, поскольку структура ПЭВП является фракталом с фрактальной размерностью d_f » 2,70 [14]. Модель такой диффузии предложена в работе [59]. В качестве модельного объекта использовано дерево Кейли, аналогом которого в полимерах является сетка макромолекулярных зацеплений. Рассмотрен вывод двух вероятностей: р - вероятности того, что диффундирующая частица (в нашем случае - молекула О₂) достигает точки на дереве, расположенной на расстоянии l от начала движения частицы, и р₀ - вероятности того, что частица на расстоянии l станет неподвижной, т.е., будет захвачена «мертвым» ответвлением дерева. Такими ответвлениями в полимерах являются свисающие цепи, разветвления цепи, боковые группы и т.д. Величину р₀ и связанные с ней параметры можно рассчитать согласно уравнениям (2.45) ¸ (2.48). Отметим, что из уравнений (2.45) и (2.46) следует, что диффузия частицы (молекулы О₂) замедляется по мере того, как она уходит от начальной точки. Это объясняется тем, что с удалением от начала растет вероятность захвата частицы «мертвым» концом. Теперь можно рассчитать р₀, используя полученные согласно уравнениям (2.46) и (2.48) величины химических размерностей структуры полимера d_l и ее скелета (d_l = 2,70,  = 1,0) и предположив в уравнении (2.45) величину А = 0,06. Такое предположение обусловлено чисто математическими соображениями: поскольку р₀ £ 1,0, то l^a ³ A. Для образцов толщиной 0,4 мм l = 0,2 мм, l^a » 0,065 и это обусловило выбор А. Тогда расчет по уравнению (2.45) дает р₀ = 0,074 для пленок и р₀ = 0,982 - для массивных образцов. Сравнение этих вероятностей демонстрирует, что в тонких образцах практически все молекулы О₂ принимают участие в формировании карбоксильных групп, тогда как в массивных образцах только 2 молекулы из 100 доходят до медианной плоскости образца. В реальности это соотношение будет еще меньше, поскольку при его оценке не учитывалась возможность реакции О₂ с реакционноспособными центрами макромолекул ПЭВП.

Вероятность р(l) дается следующим соотношением [59]:

,                                         (5.24)

где параметр В определен так [59]:

.                                                          (5.25)

Для линейного ПЭВП  = 1,0 и, используя полученную выше константу А= 0,06, определяем р= 0,463 для пленок и р = 0,0092 для масcивных образцов. Из приведенной оценки следует, что, грубо говоря, в пленочных образцах до медианной плоскости доходит каждая вторая молекула О₂, тогда как в массивных образцах - только одна из 109 молекул О₂. Если учесть, что в массивном образце макромолекул и, следовательно, реакционноспособных центров, на порядок больше, чем в пленочных, то это дает различие примерно на 3 порядка, наблюдаемое между значениями t_d и [55].

В заключение укажем одно теоретическое предсказание, следующее из рассмотренной выше модели [59]. Член в скобках в уравнении (5.24) появляется из-за того, что в случае ветвления скелета дерева Кейли (в рассматриваемом случае это означает разветвленный или сшитый полимер), т.е.,  > 1, частица сносится туда, где эти ветвления происходят чаще. Условие < 1 означает В > 0 и вероятность р(l) ожидается выше для разветвленных (сшитых) полимеров по сравнению с линейными. Оценка значений р₀ и р при = 1,3 и неизменных прочих параметрах дала следующие результаты: для пленок р₀ = 0,429 и р = 0,50, для массивных образцов - р₀ = 0,977 и р = 0,0123. Следовательно, наиболее существенным является различие р₀ для пленок сшитых и линейных полимеров: предсказывается сток молекул О₂ на поперечные связи, т.е., предполагается, что в процессе теплового старения сшитого ПЭВП будет разрушаться сетка химических связей. Остальные вероятности меняются незначительно [54].

Таким образом, изложенные выше результаты показали, что наиболее вероятной причиной различия скоростей термоокислительной деструкции для тонких и массивных образцов ПЭВП является замедление диффузии кислорода для последних. Этот эффект обусловлен закономерностями протекания аномальной диффузии на фрактальной структуре ПЭВП. Количественные оценки продемонстрировали, что методы классического анализа не объясняют различия величин индукционного периода для кинетического и диффузионного режимов термоокислительной деструкции ПЭВП, тогда как методы фрактального анализа дают правильный порядок этого различия.

Вкратце подводя итоги изложенных в главе 5 результатов исследований, следует отметить, что наиболее важным структурным фактором в процессе термоокислительной деструкции твердофазных полимеров является эффективная степень связности структуры, характеризуемая эффективной спектральной размерностью . Наличие временного (энергетического) беспорядка увеличивает  по сравнению со структурами, обладающими только пространственным беспорядком, что приводит к усилению термоокислительной деструкции. Пример уменьшения  относительно d_s для композиций ПЭВП + Z показывает возможность регулирования этого параметра в желательном направлении.