Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАЦИОНАРНЫЕ МАШИНЫ

Долганов А. В.,

7.7. Кинематика и динамика подъема

В кинематике подъемных установок рассматриваются скорости, ускорения и пути подъемных сосудов в функции времени (рис. 7.6). Канатные подъемные установки работают циклически: за периодом движения сосудов продолжительностью tд следует пауза длительностью θ, необходимая для загрузки и разгрузки подъемных сосудов [1].

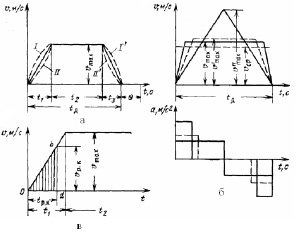
За период пуска подъемной машины скорость движения сосудов и канатов изменяется от нуля до максимального значения vmax. На этой скорости подъемные сосуды перемещаются в течение определенного времени, а затем, при подходе сосудов к приемным площадкам, их скорость уменьшается до нуля. Графическое изображение скорости v сосуда в функции времени t называют тахограммой подъема или диаграммой скорости (рис. 7.6, а).

Тангенс угла наклона касательной к любой точке кривой v = ƒ(t) представляет собой ускорение подъемного сосуда а = tgγ = dv/dt. Высота подъема равна площади, ограниченной кривой на диаграмме скорости

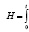vdt (7.28)

В общем случае в период разгона и замедления сосудов их ускорение переменное и скорость изменяется не пропорционально времени, т. е. не линейно.

Если законы изменения ускорений во время разгона и замедления подъемной машины одинаковы, то диаграмма скорости может иметь выпуклые (кривые I и I’) или вогнутые (кривые II и II’) бока. При постоянной величине ускорений скорость изменяется линейно и ее диаграмма имеет вид трапеции (показана сплошной линией). Возможны также варианты диаграмм скорости с различным изменением ускорений при разгоне и торможении, в частности, с возрастающими ускорением при разгоне (кривая II) и замедлением при торможении (кривая I’), с постоянным ускорением во время разгона (сплошная линия) и уменьшающейся величиной ускорения при замедлении (кривая II’) и т. п.

Наиболее удобными в большинстве случаев оказываются диаграммы скорости с постоянной величиной ускорения во время разгона и замедления машины. Они реализуются при использовании в качестве приводных двигателей подъемных машин асинхронных электродвигателей. Поэтому такие диаграммы и получили наибольшее распространение на практике. Значительно реже применяются диаграммы с вогнутыми боками и почти не применяются с выпуклыми боками, так как они приводят к возникновению максимальных динамических усилий в канате.

Для простоты изложения ограничимся рассмотрением диаграмм с постоянными ускорениями и замедлениями на участках разгона и торможения подъемных машин.

Трехпериодные диаграммы подъема
при постоянном радиусе органа навивки

При заданной высоте подъема Н (площади тахограммы) и длительности подъема сосудов tд можно построить бесчисленное множество тахограмм, которые будут отличаться различными значениями времени t1 разгона, времени t2 движения сосуда с vmax и времени t3 торможения сосуда. При этом будут изменяться максимальная скорость подъема и значения ускорений, что легко видеть из рис. 7.6, б, на котором движения сосудов для упрощения приняты в переходные периоды равноускоренными и равнозамедленными, т. е. есть для каждого периода а = const.

В пределе при длительном разгоне и торможении отсутствует на тахограмме период t2 движения сосуда с постоянной скоростью и тахограмма из трехпериодной превращается в двухпериодную. При этом максимальная скорость vmax достигнет наибольшего значения. Значение vmax будет уменьшаться с увеличением времени t2 движения сосуда с постоянной скоростью vmax<v’max<v’’max.

Предельное минимальное значение vmax = vср будет в теоретическом случае, если бы разгон и замедление сосудов происходили мгновенно, т. е. t1 и t2 равнялись бы нулю.

При трапецеидальной диаграмме скорости vmах изменяется в пределах

vср < vmax < 2vср (7.29)

В теории подъема для оценки тахограмм используется показатель неполноты тахограмм – множитель скорости α (см. выше)

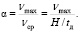(7.30)

Для трехпериодных диаграмм этот показатель с учетом пределов изменения vmax лежит в пределах 1 < α < 2.

При полноте диаграммы α = 2 диаграмма двухпериодная (см. рис. 7.6, б), t2=0, ускорение и замедление минимальны, но такая диаграмма неприемлема из-за большой величины скорости vmax. По мере уменьшения α величина скорости vmax уменьшается, но одновременно ускорения увеличиваются. Чем ближе множитель скорости к единице, тем меньше максимальная скорость, больше ускорения и тем экономичнее работает приводной двигатель подъемной машины.

Трехпериодная трапецеидальная диаграмма подъема (см. рис. 7.6, б) применяется при клетевом подъеме.

При работе скипов с разгрузкой через дно может применяться четырехпериодная диаграмма скорости, а при опрокидных сосудах – шести- и семипериодные диаграммы.

Задачами кинематики являются расчет диаграмм скорости и выбор таких кинематических параметров, которые обеспечивали бы необходимую производительность подъемной установки при удовлетворении следующих требований: максимальные значения скоростей и ускорений не должны превышать допустимых предельных значений; кинематические параметры должны быть наивыгоднейшими по условию максимальной загрузки приводного двигателя подъемной машины.

При этом наиболее часто приходится решать две задачи кинематики: определять максимальную скорость vmax при заданных значениях высоты Н и времени подъема tд или находить время подъема tд при заданных значениях Н и vmax.

Подъемная установка представляет собой сложную электромеханическую систему, которая состоит из инерционных тел (подъемных сосудов, канатов, органов навивки редукторов, электродвигателей и др.), связанных между собой упругими элементами (канатами, валопроводами). Большие движущиеся массы установок, перемещаемые в условиях неустановившегося движения, приводят к возникновению значительных инерционных нагрузок. Эти нагрузки оказывают существенное влияние на производительность установок, величину установленной мощности приводного электродвигателя подъемной машины и выбор запасов прочности элементов подъемных установок.

Анализ динамических процессов подъемных установок в общем случае с учетом упругости элементов, распределения масс канатов по их длине, нелинейностей и рассеяния энергии весьма сложен. Поэтому для решения конкретных практических задач кинематики и динамики прибегают к упрощениям расчетных схем подъемных установок. В частности, при рассмотрении их динамики широко используется представление подъемных установок в виде одномассных систем «подъемный сосуд – канат» без учета упругости звеньев, т. е. последние принимаются абсолютно твердыми телами, не подвергающимися деформациям.

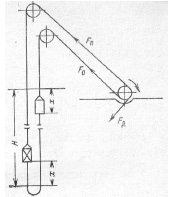
Основное уравнение. Для реализации требуемой диаграммы скорости подъемного сосуда к ветвям каната, навиваемого на барабан подъемной машины, должны быть приложены усилия Fп и F0, достаточные для преодоления инерционных нагрузок, сопротивлений перемещению подъемных сосудов и канатов (рис. 7.7) [1].

Такое допущение может быть принято только при установившемся движении подъемных сосудов, т. е. с постоянной скоростью или с постоянными ускорением и замедлением, когда отсутствуют их колебания. Рассмотрение подъемных установок как одномассных систем позволяет выбирать рациональные режимы подъемных установок и мощность приводного электродвигателя подъемной машины, пользуясь простым математическим аппаратом.

Fп = Fп.ст + Fп.дин (7.31)

Fо = Fо.ст – Fо.дин (7.32)

где Fп.ст и Fо.ст – статические составляющие, a Fп.дин и Fо.дин – динамические составляющие усилий натяжения головных канатов:

Fн.ст = g ∑mн + Rп ; Fo.ст = g ∑mo + Ro ; (7.33)

Fп.дин = a ∑mп ; Fo.дин = a ∑mo (7.34)

В периоды равномерного движения Fп.дин и Fо.дин равны нулю и Fп = Fп.ст , Fо = Fо.ст. В уравнениях (7.33) и (7.34) ∑mп – суммарная масса поднимаемых сосудов и канатов, кг:

∑mп = mг + mс + mк (Н – х) + m’к х (7.35)

∑m0 – суммарная масса опускаемых сосуда и канатов, кг;

∑mo = mс + mк’ (Н – х) + mк х (7.36)

mг, mс – соответственно масса полезного груза и сосуда, кг; mк – масса 1 м подъемного каната (одноканатные машины) или всех головных канатов (многоканатные машины), кг; m’к – масса 1 м уравновешивающего каната, кг; Н – высота подъема, м; х – путь, пройденный сосудом от начала подъема, м; Rп – сила сопротивления перемещению поднимаемых канатов и сосуда, Н; R0 – сила сопротивления перемещению опускаемых канатов и сосуда; а=d2x/dt2 – ускорение сосудов, м/с.

Особенности расчетов подъемных установок
со шкивами и барабанами трения

В подъемных установках со шкивами трения (см. рис. 7.2, в) подъем грузов осуществляется за счет сил трения, возникающих между канатами, огибающими канатоведущий орган, и поверхностями его желобков. Используя формулу Эйлера для гибкой нити, получаем следующее выражение для предельного окружного усилия трения, которое может передать шкив:

Fтр = Fo(e fa – 1) (7.37)

Требуемую величину окружного усилия, как видно из приведенной формулы, можно получить, увеличивая:

- статическое натяжение сбегающей ветви каната навеской хвостового каната;

- коэффициент трения ƒ применением специальной футеровки желобов под канат на канатоведущих органах;

- угол обхвата α применением отклоняющих шкивов.

Условием безопасной работы установок является отсутствие проскальзывания канатов относительно канатоведущего органа. Это условие определяется неравенством

Fп – Fo ≤ Fтр (7.38)

т. е. во избежание проскальзывания сила трения каната о шкив должна быть больше разности натяжений рабочих ветвей канатов. Отношение этих величин, называемое коэффициентом безопасности σ против скольжения, должно быть больше единицы:

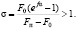(7.39)

Различают статический σст и динамический σдин коэффициенты безопасности против скольжения:

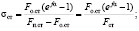(7.40)

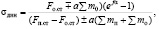(7.41)

где ∑mп и ∑mо – суммы приведенных масс подъемной установки со стороны поднимающихся и опускающихся ветвей канатов, определяются по выражениям (7.42).

В случае равновесного уравновешивающего каната (mк = m’к) получим:

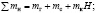
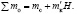(7.42)

В выражении (7.41) верхний знак относится к периоду разгона, нижний – к периоду замедления подъемной машины. Коэффициент безопасности является одним из определяющих показателей безопасности и экономичности подъемных установок с канатоведущими органами трения. С точки зрения безопасности коэффициент желательно принимать возможно большим, а для обеспечения экономичности параметров подъемной установки – возможно меньшим.

Помимо коэффициентов, определяемых выражениями (7.43) – (7.44), на практике для оценки запаса по скольжению пользуются отношением статических усилий в головных канатах:

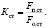(7.43)

Опытом эксплуатации подъемных установок со шкивами трения установлено, что при значениях коэффициентов трения ƒ=0,2; 0,25; 0,3 обеспечивается безопасность соответственно при Кст ≤ 0,3; 1,5; 1,75 или σст ≥ 1,5; 1,75; 2,3 [1].

При работе подъемной машины со шкивами трения ограничивается также действительное замедление aд, которое должно быть меньше критического замедления aкр, при котором начинается скольжение канатов. Рекомендуется принимать

aд ≤ 0,8 aкр (7.44)

Наиболее тяжелым из всех режимов работы является спуск груза или противовеса, для этого режима и осуществляется, в основном, проверка по допустимому замедлению. Критическое ускорение aкр для режима замедления при спуске груза имеет следующие выражения:

установка без отклоняющих шкивов

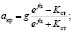(7.45)

установка с отклоняющим шкивом, когда груженая ветвь расположена со стороны отклоняющего шкива,

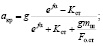(7.46)

то же, но груженая ветвь расположена на стороне, противоположной отклоняющему шкиву,

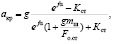(7.47)

где mш – приведенная масса отклоняющего шкива, кг.

При спуске груза последний случай расположения груженой ветви является более опасным, так как критические ускорения меньше. Из трех рассмотренных методов оценки невозможности скольжения канатов, последний метод обеспечивает наиболее точные результаты.

На подъемных установках со шкивами трения для уменьшения вероятности проскальзывания канатов применяют тяжелые хвостовые канаты.