Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

6.1. Роль структуры полимерного расплава в процессе термоокислительной деструкции

Влияние структуры полимеров в их различных состояниях на процессы термоокислительной деструкции в настоящее время является общепризнанным [1-3]. Однако количественные оценки такого влияния существуют только для твердофазных аморфно-кристаллических полимеров, при этом в качестве характеристики структуры используется степень кристалличности [3; 4]. В остальных случаях применяют полуэмпирические подходы - модель «клетки» [1], зонную модель [3] и т.д. Такое положение обусловлено отсутствием количественной структурной модели для аморфного состояния полимеров как в случае аморфных стеклообразных полимеров, так и для полимерных расплавов. Однако, появление кластерной модели структуры аморфного состояния полимеров [5; 6] и развитие в последние годы методов фрактального анализа для описания полимеров [7-9] позволяет устранить этот пробел. Поскольку кластерная структура распадается при температуре стеклования (плавления) полимеров [5; 6], то очевидно, что для полимерных расплавов фрактальный анализ в настоящее время по существу является единственным математическим аппаратом, способным описать их структуру [10].

Авторы работы [11] предприняли попытку выяснить структурные факторы, определяющие ход термоокислительной деструкции в случае полимерных расплавов. С этой целью были исследованы полиарилаты (ПАр) на основе дихлорангидрида 1,1-дихлор-2,2-ди(n-карбоксифенил) этилена и диана, а также блок-сополимеры полиарилатариленсульфоноксид (ПААСО), синтезированные из диана, смеси (1 : 1) дихлорангидридов тере- и изофталевой кислот, дигидроксилсодержащего олигоариленсульфоноксида на основе диана и 4,4¢-дихлордифенилсульфона молекулярной массы 4600. Способы поликонденсации, которыми получены указанные полимеры, и их основные характеристики приведены в табл. 6.1.

Рассмотрим параметры, характеризующие структуру полимерного расплава. Исследование процесса термоокислительной деструкции ПАр и ПААСО выполнено в интервале температуре 573 ¸ 723 К, а интервал температур стеклования этих аморфных полимеров составляет 463 ¸ 491 К (см. табл. 6.1). Из уравнения (1.43) и данных табл. 6.1 следует, что термоокислительная деструкция этих полимеров протекает при температурах, превышающих температуру перехода «жидкость 1 - жидкость 2» T_ll. Как отмечалось в предыдущей главе, при T_ll происходит переход полимерного расплава от «жидкости с фиксированной структурой» (где наблюдается остаточная структурная упорядоченность [12]) к истинно жидкому состоянию или «бесструктурной жидкости» [13]. Тем не менее, «бесструктурность» расплава при T > T_ll относится к отсутствию надмолекулярной структуры, но структура макромолекулярного клубка в расплаве остается важным структурным фактором (по существу единственным при T > T_ll) [11].

Таблица 6.1

Способы поликонденсации и основные характеристики ПАр и ПААСО [11]

Условное обозначение	Способ поликон- денсации	Df	Tc, K	, 103	Еакт, кДж/моль	Kd´104, c-1	Км
ПАр-1	Низко- температурный	2,58	471	76	71,2	0,34	-
ПАр-2	Высоко- температурный	2,61	476	72	77,5	0,26	-
ПАр-3	Межфазный	2,69	462	69	86,5	0,17	-
ПААСО-1	Низко- температурный	2,60	472	76	76,7	0,19	0,45
ПААСО-2	Высоко- температурный	2,64	474	64	79,6	0,24	0,60
ПААСО-3	Межфазный	2,84	491	66	109,0	0,07	1,70
ПААСО-4	Эмульсионный	2,78	489	58	102,6	0,11	1,50

Наиболее точно структуру макромолекулярного клубка, который является фрактальным объектом [10; 14], можно охарактеризовать с помощью его фрактальной (Хаусдорфовой) размерности D_f, описывающей распределение элементов клубка в пространстве [10]. Методы расчета величины D_f изложены в главе 1 (см. уравнения (1.47) ÷ (1.49)).

Ранее было показано [3], что зависимости , где  - количество поглощенного в процессе термоокислительной деструкции кислорода, k - степень кристалличности, от времени t для полипропилена трансформируются в прямые линии. Параметр (1 - k) определяет ту часть структуры аморфно-кристаллического полипропилена, в которой реализуются процессы термоокислительной деструкции (аморфную фазу). Для расплава ПАр и ПААСО структура характеризуется величиной D_f. Как было показано в работе [15], процессы, протекающие во фрактальных пространствах (с фрактальным временем), описываются методами дробного дифференцирования и интегрирования (более подробно см. в следующей главе). В этом случае дробный показатель n_d совпадает с фрактальной размерностью множества Кантора и указывает долю состояний системы, сохраняющихся за все время эволюции t. Напомним, что множество Кантора рассматривается в одномерном евклидовом пространстве (d = 1), поэтому его фрактальная размерность d_f < 1 в силу определения фрактала [16]. Для фрактальных объектов в евклидовых пространствах с более высокими размерностями (d > 1) в качестве n_d следует принимать дробную часть d_f (в нашем случае - D_f) [11]:

n_d = D_f - (d - 1).                                                  (6.1)

Тогда величина n_d характеризует долю фрактала (макромолекулярного клубка), сохраняющуюся в процессе деструкции. Очевидно, доля макромолекулярного клубка b_d, распадающаяся в процессе деструкции, определяется так [11]:

b_d = 1 - n_d = 1 - [D_f - (d - 1)] = d - D_f             (6.2)

или, поскольку в рассматриваемом случае d = 3,

b_d = 3 - D_f.                                                           (6.3)

Таким образом, следует предположить, что именно параметр b_d должен быть использован для нормализации  по аналогии с параметром (1 - k) в случае твердофазных аморфно-кристаллических полимеров. На рис. 6.1 и 6.2 приведены зависимости от t для ПАр и ПААСО, соответственно. Линеаризовать эти зависимости можно только при использовании в качестве абсциссы величины t^1/2. Это означает, что порядок реакции обрыва цепи для расплавов ПАр и ПААСО равен 0,5. Разные наклоны прямых на рис. 6.1 обусловлены разными константами скорости реакции [3].

Наиболее важным следствием приведенных на рис. 6.1 и 6.2 графиков является то, что их линеаризация достигнута использованием фрактального параметра (3 - D_f) или b_d. Это означает, что структура полимерного расплава описывается с помощью фрактальной размерности D_f макромолекулярного клубка так же однозначно, как и структура твердофазного аморфно-кристаллического полимера с помощью его степени кристалличности [3].

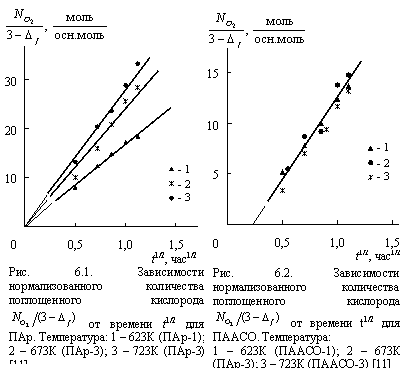
Между графиками рис. 6.1 и 6.2 существует важное различие. Прямые для пар проходят через начало координат, тогда как прямая для ПААСО смещена по оси абсцисс. Аналогичный эффект наблюдался для атактического и изотактического полипропиленов в работе [3]. Прямая для последнего смещена на некоторый промежуток времени t₀. Это смещение было объяснено линейным обрывом цепи на элементах кристаллической фазы, играющим заметную роль в самом начале реакции, когда свободные радикалы, участвующие в реакции окисления, захватываются кристаллическими образованиями, в которых кислород полностью отсутствует или его концентрация незначительна. Слишком мелкие, плохо сформированные кристаллиты не могут удерживать свободные радикалы, однако по мере увеличения размеров и повышения упорядоченности кристаллитов растет их роль как ловушек свободных радикалов, в результате чего уменьшается скорость поглощения кислорода и увеличивается период индукции окисления полимера [3]. Для рассмотренных в работе [11] полимеров это различие можно объяснить следующим образом. как было показано в работе [17], энергия активации термоокислительной деструкции при одинаковых D_f выше для ПААСО, чем для пар, из-за наличия стерических препятствий в цепи ПААСО, которыми могут быть заместители разного типа, боковые ответвления, заместители в разных положениях (пара-, орто-, мета-) и т.д. В этом случае степень влияния указанного фактора может быть определена с помощью константы Гаммета [18]. Указанные стерические препятствия могут быть ловушками свободных радикалов, как и в случае с полипропиленом [3], что уменьшает скорость поглощения кислорода и увеличивает период индукции окисления расплавов ПААСО.

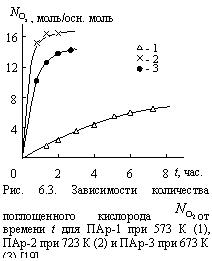
В работе [4] было получено аналитическое описание трех основных типов кинетических кривых количества поглощенного кислорода от времени t для термоокислительной деструкции. Однако, предложенные для описания кривых  уравнения носят достаточно формальный характер и входящие в них параметры получены эмпирически. Это означает, что указанные параметры не связаны со структурой полимера. Использование таких моделей затрудняет моделирование и прогнозирование процессов термоокислительной деструкции. Необходимым условием для описания кривых  с учетом структуры полимера является наличие количественной структурной модели. Как было показано выше, для полимерных расплавов структура может моделироваться в рамках фрактального анализа. Исходя из этого, авторы [19] выполнили описание кинетики термоокислительной деструкции ПАр см. табл. 6.10 в рамках двух фрактальных подходов. На рис. 6.3 в качестве примера приведены кинетические кривые поглощения кислорода   для трех исследуемых пар при трех различных температурах испытаний Т. Особенностью и этих кривых, и всех остальных кривых   для ПАр (не показанных на рис. 6.3) является то, что процесс термоокислительной деструкции протекает с замедлением как функция времени. Это является однозначным указанием на протекание процесса во фрактальном пространстве [20; 21].

В наиболее простой трактовке термоокислительную деструкцию можно представить бимолекулярной реакцией, описываемой соотношением (1.67). Скорость такой реакции k во фрактальной среде описывается соотношением (1.68). На рис. 6.4 приведена зависимость k(t) в двойных логарифмических координатах, соответствующая соотношению (1.68), для кривых , показанных на рис. 6.3. Как следует из данных этого рисунка, приведенные зависимости lnk(lnt) линейны и по их наклону можно определить величины показателя неоднородности h, которые приведены в табл. 6.2 для всех использованных ПАр и температур испытаний. Отметим значения h > 1 в интервале Т = 673 ¸ 723 К, не соответствующие указанному в работе [20] условию h £ 1. Причины такого расхождения будут рассмотрены ниже.

Теперь обратимся к фрактальной модели структуры ПАр, необходимой для количественного описания процессов термоокислительной деструкции. На рис. 6.5 приведено соотношение между h и D_f для исследуемых ПАр при четырех температурах испытаний. Как следует из приведенного графика, между h и D_f наблюдается линейное соотношение. При D_f = d = 3 h = 0, что и следовало ожидать в силу гомогенности евклидовой реакционной среды [20; 22]. Минимальное значение D_f = 2,5, которое определяется уравнением (1.44) при минимальной величине спектральной размерности d_s = 1,0 [23]. Однако, авторы [19] получили h > 1 и D_f < 2,5, что не согласуется с классическими представлениями [10; 20; 22]. Этому несоответствию можно дать следующее объяснение. Как следует из табл. 6.2 и рис. 6.5, указанные «неклассические» значения h и D_f получены при Т ³ 673К. При этих температурах начинается интенсивная термическая деструкция ПАр [19], приводящая к фрагментации и изменению химического строения макромолекулярных клубков этого полимера. Данный процесс определяет распад компактных макромолекулярных клубков ПАр на фрагменты с гораздо меньшей компактностью или снижение D_f. Как следует из уравнения (1.44), при D_f = 2 величина d_s = 0,8. Величина d_s < 1,0 означает потерю связности макромолекулярного клубка или его фрагментацию. Следовательно, при Т ³ 673К наблюдается интенсивная потеря макромолекулярным клубком своей физической структуры (потеря массы образцом в указанном интервале температур достигает 50 %), что и определяет «неклассическое» поведение параметров h и D_f. Строго говоря, в этом случае физическая трактовка уже некорректна, хотя формальное ее применение при h = 1 ¸ 2 и D_f = 2,0 ¸ 2,5 все еще возможно (рис. 6.5) [19].

 

Таблица 6.2

Температурная зависимость показателя неоднородности  h для полиарилатов [19]

Полимер	Полимер
	573К	623К	673К	723К
ПАр-1	0,50	1,0	1,24	1,76
ПАр-2	0,61	0,57	1,16	1,40
ПАр-3	0,15	0,76	1,07	2,07

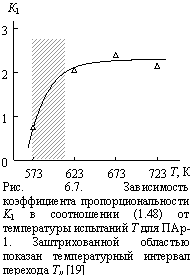
Другая фрактальная модель описания кинетики термоокислительной деструкции основана на применении соотношения (1.48). Указанное соотношение предполагает, что рост D_f означает компактизацию макромолекулярного клубка, уменьшение числа доступных для реакций мест этого клубка и, как следствие, снижение скорости реакции (в рассматриваемом случае - термоокислительной деструкции). На рис. 6.6 показано сравнение экспериментальных и рассчитанных по соотношению (1.48) (коэффициенты пропорциональности K₁ в этом соотношении выбраны методом совмещения) зависимостей  для ПАр-1 при четырех температурах испытаний. Как можно видеть, получено хорошее соответствие теории и эксперимента. Это обстоятельство указывает на то, что скорость термоокислительной деструкции расплава ПАр контролируется структурой макромолекулярного клубка, характеризуемой его фрактальной размерностью D_f [19].

На рис. 6.7 приведена зависимость константы K₁ в соотношении (1.48) от температуры испытаний Т. Как следует из приведенного графика, в интервале Т, соответствующем переходу T_ll согласно уравнению (1.43), наблюдается существенное увеличение K₁, а затем она остается примерно постоянной. Такое изменение K₁ связано с изменением вязкости расплава [9].

Следовательно, изложенные выше результаты вновь продемонстрировали, что кинетика термоокислительной деструкции полиарилата может быть точно описана в рамках фрактальных моделей. Основным структурным фактором при T > T_ll является структура макромолекулярного клубка, характеризуемая ее фрактальной размерностью D_f. Параметры h и D_f двух фрактальных моделей тесно связаны между собой. Важно отметить, что реакция окисления во фрактальном пространстве протекает значительно медленнее, чем в евклидовом.

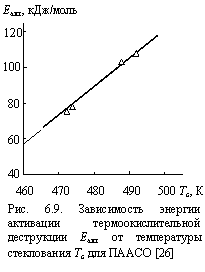
Таким образом, исследования процесса термоокислительной деструкции сополимеров ПААСО, полученных разными способами поликонденсации (см. табл. 6.1), показали, сильную зависимость характеристик деструкции от способа полимеризациии [11]. Предполагается, что такая зависимость обусловлена зависимостью структуры полимеров ПААСО от способа поликонденсации. Поскольку химическая структура ПААСО при всех способах поликонденсации идентична, то следует предположить, что указанные зависимости характеристик термоокислительной деструкции ПААСО от его способа поликонденсации обусловлены разной степенью композиционной неоднородности (микрогетерогенности), которая является одной из наиболее важных характеристик сополимеров [24]. В свою очередь, следует ожидать влияния степени композиционной неоднородности цепи сополимеров на структуру макромолекулярного клубка [25]. Исходя из этого, авторы [26] выполнили количественный анализ влияния степени композиционной неоднородности (микротегерогенности) цепи сополимера на структуру макромолекулярного клубка и, как следствие, на характеристики термоокислительной деструкции сополимеров. Проверка указанных выше предположений выполнена с привлечением методов фрактального анализа на примере ПААСО.

Как отмечалось выше, одной из наиболее важных характеристик сополимеров является регулярность строения образующихся макромолекул или их композиционная неоднородность (микрогетерогенность), количественно характеризуемая коэффициентом микрогетерогенности K_м = 0, для строго чередующегося сополимера K_м = 2,0. Между этими крайними случаями, соответствующими полностью упорядоченному расположению звеньев, лежат все возможные значения K_м, причем для полностью статистического (т.е., наиболее разупорядоченного) распределения K_м = 1,0. По абсолютной величине отклонения K_м от единицы можно количественно судить о степени упорядоченности распределения звеньев в цепи сополимера, а по тому, в какую сторону наблюдается это отклонение - о склонности мономеров (олигомеров) либо к чередованию в цепях (K_м > 1), либо к образованию длинных блоков обоих сомономеров (K_м < 1) [24].

Величину K_м можно определить с помощью уравнения Гордона-Тейлора-Вуда [27]:

,                                (6.4)

где Т_с - температура стеклования сополимера, Т_с1 и Т_с2 - температуры стеклования гомополимеров, W - мольная доля гомополимера с температурой стеклования Т_с2. Полученные согласно уравнению (6.4) значения K_м приведены в табл. 6.1.

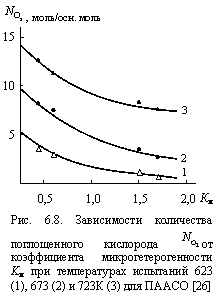
На рис. 6.8 показаны зависимости количества поглощенного кислорода   от K_м для трех температур испытаний Т. Как следует из приведенных графиков, при всех рассмотренных Т наблюдается систематическое снижение   по мере роста K_м.

На рис. 6.9 приведена зависимость энергии активации термоокислительной деструкции Е_акт (см. табл. 6.1) от температуры стеклования Т_с для ПААСО. Как можно видеть, наблюдается линейный рост Е_акт по мере увеличения Т_с. Из уравнения (6.4) следует, что увеличение Т_с в случае ПААСО обусловлено только ростом K_м, поскольку все остальные члены этого уравнения одинаковы для ПААСО, полученных разными способами поликонденсации. Таким образом, данные рис. 6.8 и 6.9 показывают систематическое снижение интенсивности процесса термоокислительной деструкции по мере роста K_м (или Т_с) для ПААСО [26].

Рассмотрим физические основы указанной тенденции. Как известно [10; 14], увеличение фрактальной размерности приводит к повышению плотности объекта. Исходя из этого, следует ожидать уменьшения поглощения кислорода  по мере роста D_f. На рис. 6.10 приведена зависимость D_f(K_м) для ПААСО. Как можно видеть, эта зависимость линейна и наблюдается увеличение D_f от 2,5 при K_м = 0 до ~ 2,95 при K_м = 2,0. Из уравнения (1.44) следует, что минимальное значение D_f при минимальной величине d_s = 1 [23] равно 2,5, а максимальное (теоретическое) значение D_f = d = 3 [14]. Однако, как показал Баланкин [28], для реальных физических объектов величина фрактальной размерности не может превышать 2,95. Таким образом, данные рис. 6.10 указывают на превосходное соответствие точно определенных интервалов существования параметров K_м и D_f: K_м = 0 ¸ 2,0 и D_f = 2,50 ¸2,95 [26]. График D_f(K_м), показанный на рис. 6.10, позволяет получить аналитическую взаимосвязь D_f и K_м [26]:

D_f = 2,50 + 0,225 K_м                                          (6.5)

Следовательно, приведенные выше данные предполагают рост D_f (и соответствующее повышение компактности макромолекулярного клубка) по мере увеличения K_м. Понять физический смысл этой тенденции можно в рамках компьютерного моделирования фрак-тальной необратимой агрегации. Так, увеличение Т_с по мере роста K_м, следующее из уравнения (6.4), предполагает увеличение энергии когезии сополимеров [29] или усиление взаимодействий притяжения между элементами макромолекулярного клубка. В свою очередь, усиление указанных взаимодействий определяет повышение плотности и уменьшение радиуса инерции R_g фрактального агрегата (в нашем случае - макромолекулярного клубка) [30]. И, наконец, следует учитывать еще один фактор, тесно связанный с предыдущими. Хорошо известно [31], что в химических реакциях большое значение имеет стерический фактор р (р £ 1), показывающий, что не все соударения происходят с надлежащей для образования продукта реакции ориентацией реагирующих молекул. В процессах термоокислительной деструкции стерическому фактору следует придать несколько иной физический смысл, аналогичный используемому в процессах газопереноса [32]. В этом случае фактор р учитывает сопротивление, создаваемой структурой полимера, потоку газообразного или жидкого оксиданта. Чем меньше р, тем выше сопротивление структуры и тем более затруднен доступ оксиданта к реакционноспособным центрам макромолекул полимера. По существу, это положение лежит в основе понятия «структурная стабилизация» [2].

Величину р можно оценить с помощью следующего соотношения [33]:

,                                                  (6.6)

где R - универсальная газовая постоянная.

Предэкспоненциальный множитель р_а в соотношении (6.6) определяется с помощью двух граничных условий. Одно из них дает определение р: р £ 1. Расчет р при выполнении указанного условия показал, что зависимости (р) представляют собой семейство прямых, параллельных друг другу, причем каждая прямая описывает данные для одной температуры испытаний Т. Далее было использовано второе условие: предполагалось, что для наименьшей Т = 573 К величина исходного содержания кислорода  равна ~ 2,5 моль О₂/осн. моль. Построенные указанным образом зависимости (р) обнаружили, что увеличение Т приводит к существенному росту : от 2,5 до 13,5 моль О₂/осн. моль в интервале Т = 573 ¸ 723 К. Эффект увеличения   по мере роста р значительно слабее.

Исходя из приведенных выше соображений, следует ожидать, что увеличение компактности макромолекулярного клубка, характеризуемой его плотностью r, приведет к повышению сопротивления клубка переносу оксиданта, характеризуемого величиной р. двойная логарифмическая зависимость р(r) для пар и ПААСО при двух температурах испытаний подтверждает это предположение (рис. 6.11). Величина r оценена согласно фрактальному соотношению (2.22), где значение R_g было произвольно принять равным 100 относительных единиц, поэтому r также получена в относительных единицах. Зависимость р(r) аналитически описывается так:

р = 1 - r^0,224.                                                       (6.7)

Расчет величины р согласно уравнению (6.6) показал уменьшение предэкспоненциального множителя р_а от ~ 10⁶ до ~ 0,25 ´ 10⁶ по мере роста Т от 573 до 723К. Функциональная связь р с Т осуществляется в виде «больцмановского» фактора, что позволяет установить конкретную форму, в которой тепловое движение влияет на процесс термоокислительной деструкции [34]. В рамках клеточной модели предполагается [1], что реакция окисления может произойти тогда, когда в сферу действия реационноспособной частицы попадает центр второй активной частицы. Этот процесс по своему физическому смыслу аналогичен появлению энергетической флуктуации [34]. Средний промежуток времени t_фл между двумя последовательными флуктуациями величиной Е_акт согласно (6.6) описывается выражением [34]:

.                                                               (6.8)

Корреляция между t_фл и р для ПАр и ПААСО при Т = 623К показала (рис. 6.12), что наблюдается очень сильная зависимость t_фл от р даже в логарифмических координатах. При р ® 0 величина t_фл быстро растет, а при р ® 1 стремится к нулю. Это означает, что при р ® 0 промежуток времени между двумя последовательными актами термического окисления полимера резко увеличивается и, следовательно, процесс термоокислительной деструкции сильно замедляется, а при р ® 1 - наоборот. Такая зависимость lnt_фл(р) наглядно иллюстрирует сильное влияние р на скорость термоокислительной деструкции.

Также обнаружен линейный рост lnt_фл по мере увеличения D_f (рис. 6.13). Зависимость lnt_фл(D_f) демонстрирует структурный аспект термоокислительной деструкции расплава полимеров: увеличение компактности макромолекулярного клубка, характеризуемое ростом D_f, приводит к увеличению t_фл и, следовательно, к замедлению термоокислительной деструкции.

Таким образом, изложенные выше результаты показали, что увеличение регулярности строения цепей сополимеров, выражаемое ростом K_м, приводит к усилению взаимодействий притяжения элементов макромолекулярного клубка и увеличению его фрактальной размерности. Оба указанных фактора способствуют увеличению плотности клубка, т.е., повышению его компактности. Этот эффект определяет снижение интенсивности процесса термоокислительной деструкции сополимеров. Кроме того, обнаружено сильное влияние на скорость этого процесса стерического фактора р, характеризующего сопротивление структуры полимерного расплава процессам переноса оксиданта. В свою очередь, величина р также определяется структурой макромолекулярного клубка, характеризуемой его фрактальной размерностью D_f. Промежуток времени между двумя последовательными актами термоокислительной деструкции является функцией р и, следовательно, D_f [26].

В заключение этого раздела рассмотрим физический смысл константы скорости реакции в евклидовом и фрактальных пространствах. Как известно [3], константа скорости реакции k_d широко используется в кинетике химических реакций, в том числе и при описании термоокислительной деструкции, как показатель скорости протекания реакции. Поэтому необходимость указанного исследования следует в силу как важности этого показателя в описании термоокислительной деструкции, так и его применения для расчета фрактальной размерности D_f (см. уравнения (1.47) и (1.49)). Наиболее простое уравнение, связывающее скорость реакции dQ/dt и степень конверсии (преобразования) Q c k_d, имеет вид [3]:

,                                        (6.9)

где t - время; n - порядок реакции.

В случае n = 1 (реакция первого порядка) величину k_d легко получить из уравнения (6.9). Однако, развитие в последние годы фрактальной кинетики химических реакций [20; 22; 35] позволяет уточнить наши представления о параметре k_d, что и было выполнено в работе [36] на примере термоокислительной деструкции ПААСО.

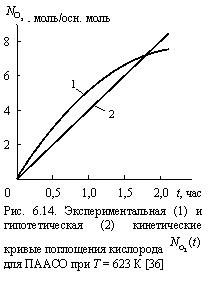
На рис. 6.14 приведена экспериментальная кинетическая кривая поглощения кислорода   для ПААСО, а также гипотетическая линейная зависимость   примерно с такими же параметрами. Отметим, что зависимости   линейного типа также встречаются на практике (например, для поликарбоната на основе бисфенола А [37]). Причины сравнения двух указанных типов зависимостей   будут рассмотрены ниже.

Рассмотрим оценку константы скорости термоокислительной деструкции k_d для экспериментальной кривой  рис. 6.14 согласно уравнению (6.9). Величину степени превращения Q можно оценить как отношение [38]:

,                                                           (6.10)

где   - предельное количество кислорода, способного поглотиться при окислении.

В рамках химического анализа структуры ПААСО было показано [38], что при условии окисления всех метильных и алифатических групп величина  = 24,1 моль О₂/осн. моль. На рис. 6.15 приведена зависимость dQ/dt от (1 - Q), где величина Q оценена по уравнению (6.10). Как можно видеть, эта зависимость криволинейна, что исключает определение k_d из наклона этого графика согласно общепринятой методике.

Другой способ оценки Q получен в рамках фрактального анализа. Как показано в работе [11], величина n_d (см. уравнение (6.1) характеризует долю фрактала (макромолекулярного клубка), сохраняющуюся в процессе деструкции. Это предполагает, что доля подвергающейся деструкции части макромолекулярного клубка равна (1 - n_d) и, следовательно, реальную величину предельного количества кислорода, способного поглотиться при окислении, следует записать как (1-n_d), где , как и ранее равно 24,1 моль О₂/осн. моль. Тогда величина Q определяется так [36]:

.                                              (6.11)

На рис. 6.15 также приведена зависимость dQ/dt от (1 - Q) для ПААСО, где величина Q рассчитана по уравнению (6.11). В такой трактовке указанная зависимость дает линейный график, из наклона которого можно определить константу скорости реакции k_d » 2,86 ´ 10^-4 c^-1 [36].

Теперь рассмотрим общие условия получения постоянной величины k_d, т.е., условия реализации критерия k_d = const. Из уравнения (6.9) следует, что по мере протекания термоокислительной деструкции величина Q растет и, следовательно, величина (1 - Q) уменьшается. Это предполагает, что для достижения критерия k_d = const необходимо уменьшение dQ/dt по мере роста t. Как показано в работах [20; 22], такое снижение dQ/dt возможно только для неоднородных (фрактальных) сред (см. уравнение (1.68)). Из данных рис. 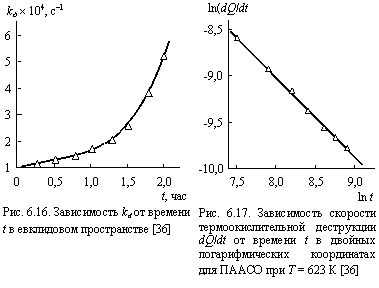6.14 очевидно, что линейная зависимость  описывает случай однородных (евклидовых) сред с h = 0 и dQ/dt = const. Зависимость k_d(t) для этой кинетической кривой   показана на рис. 6.16. Как можно видеть, наблюдается быстрый рост величины k_d (которую уже нельзя называть константой скорости реакции) по мере увеличения t [36].

На рис. 6.17 показана зависимость dQ/dt(t) в двойных логарифмических координатах, соответствующая соотношению (1.68), для ПААСО. Как можно видеть, эта зависимость линейна и ее наклон отличен от нуля, что подтверждает протекание термоокислительной деструкции ПААСО в неоднородной (фрактальной) среде.

В рамках уравнения (6.9) существует еще один вариант реализации критерия k_d = const при условии dQ/dt = const: это снижение порядка реакции n по мере роста t. Оценки показали, что критерий k_d = const реализуется при снижении n от 4,62 при t = 0,5 час. до 0,61 при t = 2,0 час. Однако, как показано в работе [35], Величина n связана с показателем неоднородности h уравнением (5.18). Для евклидовых (однородных) сред h = 0 [22] и из уравнения (5.18) следует, что в них могут протекать только реакции второго порядка. Это означает, что в евклидовых средах реализация критерия k_d = const за счет изменения порядка реакции n невозможна [36].

Таким образом, понятие константа скорости реакции» применимо только для фрактальных реакций, т.е., либо реакций фрактальных объектов, либо реакций, протекающих во фрактальных средах. Для евклидовых сред величина k_d является функцией времени, увеличиваясь по мере протекания реакции. В этом случае самоопределение k_d как константы скорости реакции теряет свой физический смысл [36].

Общим выводом на основе результатов, изложенных в настоящем разделе, является следующий постулат: все основные характеристики процесса термоокислительной деструкции полимерного расплава определяются его структурой, которая при Т ³ t_ll характеризуется фрактальной размерностью отдельного макромолекулярного клубка [38].