
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.2. Скейлинговый анализ термоокислительной деструкции
Концепции скейлинга широко применяются в физике полимеров [39] и было показано, что они могут быть использованы для описания химических реакций [40]. Понятие о скейлинге (масштабной инвариантности) у исследователей разных направлений весьма различается. Ниже будет использована точка зрения Де Женна [39], согласно которой следует максимально, насколько это возможно, абстрагироваться от деталей структуры рассматриваемой системы и выделять простые универсальные признаки, характерные для широкого класса систем. Скейлинговый закон всегда определяет только некоторую асимптотику, применимость которой, учитывая специфику системы, необходимо анализировать конкретно для каждого случая. Примером скейлинговой характеристики (скейлингового индекса) может служить фрактальная размерность, которая, как показано для регулярных фракталов, зависит только от механизма образования объекта и определяет глобальную структуру системы - распределение массы в зависимости от масштаба [41].
В настоящем разделе для анализа термоокислительной деструкции полимерных расплавов будут использованы два скейлинговых подхода. Первый из них [40] в качестве примера рассматривает реакцию, в которой частицы р химического вещества диффундируют в среде, содержащей случайно расположенные статические ненасыщенные ловушки Т. При контакте частицы Р с ловушкой Т частица исчезает. Ненасыщаемость ловушки означает, что реакция Р + Т → Т может повторяться бесконечное число раз. Обычно считается, что, если концентрация частиц и ловушек велика или реакция происходит при интенсивном перемешивании, процесс может рассматриваться как классическая реакция первого порядка. В этом случае можно считать, что закон спада концентрации частиц со временем с(t) будет иметь вид [40]:
c(t) » exp(-At), (6.12)
где А - константа, пропорциональная концентрации ловушек.
Однако, если концентрация случайно расположенных ловушек мала, с необходимостью существуют области пространства, практически свободные от ловушек. Частицы, попавшие в эти области, могут достичь ловушек лишь за весьма большое время и, следовательно, спад их числа со временем будет более медленным. Формальный анализ этой задачи показывает, что концентрация частиц спадает по закону [40]:
![]() , (6.13)
, (6.13)
зависящему от размерности пространства d (B - константа).
Нужно отметить, что сингулярная зависимость от времени в уравнении (6.13) появляется одновременно с крупномасштабными флуктуациями (неоднородностью) плотности ловушек. Если ловушки могут двигаться, то их движение как бы усредняет влияние пространственной неоднородности, так что предположения, приводящие к выражению (6.12), будут выполняться лучше. Было показано, что в этом случае концентрация частиц спадает по комбинированному закону [40]:
![]() , (6.14)
, (6.14)
где А пропорционально коэффициента диффузии ловушек.

Авторы работ [42-44] выполнили описание кинетики поглощения кислорода в процессе термоокислительной деструкции ПААСО в рамках скейлингового подхода. Полученные разными способами поликонденсации ПААСО являются удобным объектом исследования, поскольку при одинаковом химическом строении они обнаружили разные кривые ![]() не только в количественном, но и качественном отношении, т.е., они имеют разные типы кривых
не только в количественном, но и качественном отношении, т.е., они имеют разные типы кривых ![]() - с автоускорением и автозамедлением [4]. На рис. 6.18 приведены три исследуемые кинетические кривые
- с автоускорением и автозамедлением [4]. На рис. 6.18 приведены три исследуемые кинетические кривые ![]() для ПААСО. Как можно видеть, при Т = 623 К кривые
для ПААСО. Как можно видеть, при Т = 623 К кривые ![]() для этих сополимеров различаются по типу: для ПААСО-1 (условные обозначения соответствуют табл. 6.1) кривая
для этих сополимеров различаются по типу: для ПААСО-1 (условные обозначения соответствуют табл. 6.1) кривая ![]() имеет автозамедленный характер, а для ПААСО-3 - автоускоренный. Кривая
имеет автозамедленный характер, а для ПААСО-3 - автоускоренный. Кривая ![]() для ПААСО-1 при Т = 723 К также имеет автозамедленный характер, но с гораздо большим градиентом изменения
для ПААСО-1 при Т = 723 К также имеет автозамедленный характер, но с гораздо большим градиентом изменения ![]() по мере роста t. Рассмотрим скейлинговую трактовку показанных на рис. 6.18 кривых
по мере роста t. Рассмотрим скейлинговую трактовку показанных на рис. 6.18 кривых ![]() с использованием уравнений (6.12) ¸ (6.14) [40]. На рис. 6.19 приведены зависимости с(t) согласно уравнениям (6.12) и (6.13) для ПААСО-1 при Т = 623 К (режим автозамедления), где величина с определена как разность
с использованием уравнений (6.12) ¸ (6.14) [40]. На рис. 6.19 приведены зависимости с(t) согласно уравнениям (6.12) и (6.13) для ПААСО-1 при Т = 623 К (режим автозамедления), где величина с определена как разность ![]() . Как следует из данных рис. 6.19, зависимости с(t), построенные согласно обоим упомянутым уравнениям, прямолинейны, т.е., эти уравнения корректно описывают процесс термоокислительной деструкции ПААСО-1. Это означает, что в рассматриваемом случае имеет место промежуточная концентрация частиц (молекул кислорода) и ловушек (реакционноспособных центров макромолекул), причем последние, как и следовало ожидать, неподвижны.
. Как следует из данных рис. 6.19, зависимости с(t), построенные согласно обоим упомянутым уравнениям, прямолинейны, т.е., эти уравнения корректно описывают процесс термоокислительной деструкции ПААСО-1. Это означает, что в рассматриваемом случае имеет место промежуточная концентрация частиц (молекул кислорода) и ловушек (реакционноспособных центров макромолекул), причем последние, как и следовало ожидать, неподвижны.

На рис. 6.20 показаны зависимости с(t), построенные согласно уравнениям (6.12) ¸ (6.14), для ПААСО-1 при Т = 723К. В отличие от графиков рис. 6.19 для этого же сополимера, но при более низкой температуре, ни одно из указанных уравнений не описывает экспериментальные данные. Как показано в работах [45; 46] на примере реакции сшивания эпоксиполимеров, это означает, что реакция протекает не в евклидовом, а во фрактальном пространстве с размерностью df. В рассматриваемом случае фрактальное пространство реакции формируется фрактальной структурой макромолекулярного клубка и поэтому df = Df [43]. Далее в показателе правой части уравнения (6.13) следует заменить евклидову размерность d на фрактальную размерность Df. На рис. 6.21 показана зависимость с(t) для ПААСО-1 при Т = 723 К, соответствующая уравнению (6.13) с описанной выше заменой. Как можно видеть, в этом случае получена линейная зависимость lnc от t, т.е., процесс окисления протекает при малой концентрации молекул кислорода во фрактальном пространстве. На первый взгляд представляется, что повышение температуры от 623 до 723 К вызывает изменение характера реакционной среды от евклидова к фрактальному. Однако, более детальный анализ показал, что вопрос заключается в величине Df или, точнее, близости размерности Df к d, что определяет близость численных значений показателя в уравнении (6.13) при использовании Df и d. Так, для ПААСО-1 при Т = 623 К Df = 2,6, а при Т = 723 К Df = 2,2 [47].Соответственно, в первом случае различие величин ![]() и
и ![]() не превышает 2 %, а во втором - это различие больше 7 %. Поэтому построение зависимости lnс
не превышает 2 %, а во втором - это различие больше 7 %. Поэтому построение зависимости lnс ![]() для ПААСО-1 при Т = 623 К показало, что эти зависимости для евклидова (d = 3) и фрактального (Df = 2,6) пространств практически описываются одной линейной корреляцией. Для ПААСО-1 при Т = 723 К различие для случаев d = 3 и Df = 2,2 уже очевидно, что следует из сравнения графиков рис. 6.20 и 6.21, построенных согласно уравнению (6.13) [44].
для ПААСО-1 при Т = 623 К показало, что эти зависимости для евклидова (d = 3) и фрактального (Df = 2,6) пространств практически описываются одной линейной корреляцией. Для ПААСО-1 при Т = 723 К различие для случаев d = 3 и Df = 2,2 уже очевидно, что следует из сравнения графиков рис. 6.20 и 6.21, построенных согласно уравнению (6.13) [44].
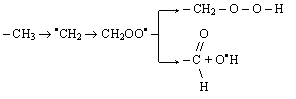
И, наконец, на рис. 6.22 приведены зависимости c(t), построенные согласно уравнениям (6.12) ¸ (6.14), для ПААСО-3 при Т = 623 К, т. е. для автоускоренного режима. Из приведенных графиков следует, что уравнения (6.12) и (6.13) не описывают поведения ПААСО-3 в режиме автоускорения, тогда как линейность зависимости с(t), построенной согласно уравнению (6.14), показывает корректность применения последнего уравнения в данном случае. Это означает, что ловушки могут двигаться, равно как и частицы. Следовательно, поскольку в режиме автоускорения термоокислительная деструкция протекает за счет реакции радикалов [3], то их высокая подвижность предполагает, что в случае ПААСО реагируют низкомолекулярные радикалы. Возможный химический механизм образования таких радикалов в случае высокотемпературного окисления обсужден в работе [3]. Предполагается, что ответственным за автоускорение продуктом являются альдегидные группы, образующиеся из метильных групп по схеме [3]:
 (6.15)
(6.15)
окисление альдегидных групп, протекающее по схеме [3]:
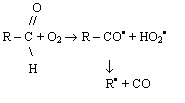 (6.16)
(6.16)
приводит к образованию активных свободных радикалов R· и низкомолекулярных радикалов НО2· [3].

Авторы [48] для описания кинетики термоокислительной деструкции ПААСО использовали комбинированный вариант уравнения (6.13) с применением фрактальной модели [20; 22]. Это означает замену в указанном уравнении размерности Df, характеризующей распределение элементов макромолекулярного клубка в пространстве, на размерность ds, характеризующую связность структуры клубка. В работе [49] было показано, что для идеальных фантомных каркасов справедливо соотношение:
![]() . (6.17)
. (6.17)

![]() , (6.18)
, (6.18)
где В2 - константа.
На рис. 6.23 показана зависимость c(t), соответствующая соотношению (6.18), которая оказалась криволинейной и поэтому не адекватной для описания кинетической кривой ![]() для ПААСО-1 (кривая 2 рис. 6.18). Причины этого несоответствия рассмотрены в работе [20] и состоят в следующем. Как известно [23], размерность ds описывает только геометрическую связность фрактала, тогда как для реальных конденсированных сред не менее важен учет временного (энергетического) беспорядка. Для описания последнего эффекта используется эффективная спектральная размерность [20; 22], определяемая из уравнения (1.72). На рис. 6.23 приведена зависимость с(t), построенная согласно соотношению (6.18), но с заменой показателя ds/2 на /2. Как можно видеть, в этом случае удалось линеаризовать функцию c(t). Таким образом, комбинированным методом описания реакции окисления во фрактальном пространстве является использование соотношения [48]:
для ПААСО-1 (кривая 2 рис. 6.18). Причины этого несоответствия рассмотрены в работе [20] и состоят в следующем. Как известно [23], размерность ds описывает только геометрическую связность фрактала, тогда как для реальных конденсированных сред не менее важен учет временного (энергетического) беспорядка. Для описания последнего эффекта используется эффективная спектральная размерность [20; 22], определяемая из уравнения (1.72). На рис. 6.23 приведена зависимость с(t), построенная согласно соотношению (6.18), но с заменой показателя ds/2 на /2. Как можно видеть, в этом случае удалось линеаризовать функцию c(t). Таким образом, комбинированным методом описания реакции окисления во фрактальном пространстве является использование соотношения [48]:
![]() , (6.19)
, (6.19)
где В3 - еще одна константа.
Несколько отличающийся от вышеописанного скейлинговый подход использовали авторы работы [50] для исследования термоокислительной деструкции ПАр и ПААСО. В настоящее время предполагается [4], что тип кинетической кривой ![]() определяется химическим строением полимера и температурой испытаний. Однако, в такой трактовке не учитываются структурные аспекты, которые, как показано выше, играют определяющую роль при реализации того или иного типа кривых .
определяется химическим строением полимера и температурой испытаний. Однако, в такой трактовке не учитываются структурные аспекты, которые, как показано выше, играют определяющую роль при реализации того или иного типа кривых .![]()
В последние 20 лет большое внимание уделялось физическим аспектам протекания реакций типа (4.32) и (4.34) [51-55]. Было показано, что эти реакции могут быть описаны степенной функцией вида:
rА ~ tx, (6.20)
где rА - количество вещества А, прореагировавшего за время t, х - показатель.
Величина показателя х зависит от ряда факторов: пространства, в котором протекает химическая реакция (евклидового или фрактальное [53]), размерностей, характеризующих эти пространства, и типа реакций (моно- или бимолекулярная реакция). Поэтому, исследуя реакции окисления в рамках концепций [51-55], можно получить более полное представление об условиях их протекания [50].
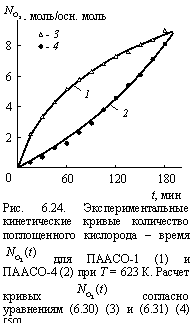
На рис. 6.24 показаны две кинетические кривые ![]() для ПААСО-1 и ПААСО-4 (условные обозначения согласно табл. 6.1) при температуре испытаний Т = 623К. Как можно видеть, эти кривые относятся к разным типам: для ПААСО-1 это кривая автозамедленного типа, для ПААСО-4 - автоускоренного. Поскольку речь идет об окислении одного и того же полимера при одной и той же температуре, то был сделан вывод [50], что изменение типа кривой обусловлено различиями структуры расплавов ПААСО-1 и ПААСО-4.
для ПААСО-1 и ПААСО-4 (условные обозначения согласно табл. 6.1) при температуре испытаний Т = 623К. Как можно видеть, эти кривые относятся к разным типам: для ПААСО-1 это кривая автозамедленного типа, для ПААСО-4 - автоускоренного. Поскольку речь идет об окислении одного и того же полимера при одной и той же температуре, то был сделан вывод [50], что изменение типа кривой обусловлено различиями структуры расплавов ПААСО-1 и ПААСО-4.
![]() , (6.21)
, (6.21)
где x - характеристический размер макромолекулярного клубка объемом vкл [53]:
![]() . (6.22)
. (6.22)
Частицы низкомолекулярного вещества (молекулы оксиданта, радикалы и т.д.) двигаются по фракталу случайным блужданием с размерностью dW, что позволяет записать [53]:
![]() . (6.23)
. (6.23)
Окончательно для реакции типа (4.32) получим:
![]() . (6.24)
. (6.24)
Для евклидовых пространств с размерностью Df = d и dw = 2 [53] получим:
![]() , (6.25)
, (6.25)
Для реакции типа (4.34) соотношение (6.25) видоизменяется следующим образом [53]:
![]() . (6.26)
. (6.26)
Как известно [23], показатель в соотношении (6.24) можно записать следующим образом:
![]() . (6.27)
. (6.27)
Далее из сочетания соотношений (6.24) и (6.27) можно получить аналог соотношений (6.25) и (6.26) для случая протекания реакции окисления во фрактальном пространстве. Для реакции типа (4.32):
![]() , (6.28)
, (6.28)
и для реакции типа (4.34)
![]() (6.29)
(6.29)
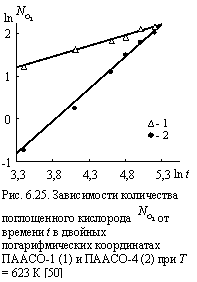
Теперь можно построить зависимости ![]() в двойных логарифмических координатах и определить показатель х в соотношении (6.20).
в двойных логарифмических координатах и определить показатель х в соотношении (6.20).
На рис. 6.25 такие зависимости приведены для кривых ![]() , показанных на рис. 6.24, т.е., автоускоренного и автозамедленного типов. Как можно видеть, в обоих случаях полученные зависимости линейны, т.е., адекватно описываются уравнениями типа соотношения (6.20). Для ПААСО-4 (автоускоренное окисление) величина х » 1,50. Это означает, что в данном случае при условиях d = 3 и ds = 3 возможен только один вариант: эта реакция описывается соотношением (6.25). следовательно, реакция, соответствующая автоускоренному типу кривых , представляет собой реакцию типа (4.32) в евклидовом пространстве с d = 3. Как отмечалось выше, наиболее вероятно, что частицы вещества А представляют собой низкомолекулярные подвижные радикалы (см. схемы (6.15) и (6.16)). Для ПААСО-1 (автозамедленное окисление) величина х » 0,5, а для шести испытаний ПАр и ПААСО в интервале Т = 623 ¸ 723К величина х варьируется в пределах 0,17 ¸ 0,50. Такие значения х исключают протекание этих реакций в евклидовом пространстве, где для d = 3 минимальное значение х = 0,75 (см. соотношение (6.26)). По этой же причине следует исключить протекание реакций во фрактальных пространствах с использованием размерности ds, поскольку для них х ³ 1/3 (см. соотношения (6.28) и (6.29)). Для объяснения полученного интервала величин х в случае автозамедленного окисления используем метод теоретического расчета размерности
, показанных на рис. 6.24, т.е., автоускоренного и автозамедленного типов. Как можно видеть, в обоих случаях полученные зависимости линейны, т.е., адекватно описываются уравнениями типа соотношения (6.20). Для ПААСО-4 (автоускоренное окисление) величина х » 1,50. Это означает, что в данном случае при условиях d = 3 и ds = 3 возможен только один вариант: эта реакция описывается соотношением (6.25). следовательно, реакция, соответствующая автоускоренному типу кривых , представляет собой реакцию типа (4.32) в евклидовом пространстве с d = 3. Как отмечалось выше, наиболее вероятно, что частицы вещества А представляют собой низкомолекулярные подвижные радикалы (см. схемы (6.15) и (6.16)). Для ПААСО-1 (автозамедленное окисление) величина х » 0,5, а для шести испытаний ПАр и ПААСО в интервале Т = 623 ¸ 723К величина х варьируется в пределах 0,17 ¸ 0,50. Такие значения х исключают протекание этих реакций в евклидовом пространстве, где для d = 3 минимальное значение х = 0,75 (см. соотношение (6.26)). По этой же причине следует исключить протекание реакций во фрактальных пространствах с использованием размерности ds, поскольку для них х ³ 1/3 (см. соотношения (6.28) и (6.29)). Для объяснения полученного интервала величин х в случае автозамедленного окисления используем метод теоретического расчета размерности ![]() [56; 57], для чего применялась формула (1.72). При значениях Df = 1,9 ¸ 2,8 [47] и d = 3 получим
[56; 57], для чего применялась формула (1.72). При значениях Df = 1,9 ¸ 2,8 [47] и d = 3 получим ![]() = 0,32 ¸ 1,04. Сравнение этих величин
= 0,32 ¸ 1,04. Сравнение этих величин ![]() и приведенных выше значений х показывает, что между ними существует соотношение х =
и приведенных выше значений х показывает, что между ними существует соотношение х = ![]() /2 в пределах погрешности определения этих параметров. Таким образом, кинетические кривые автозамедленного типа представляют реакцию типа (4.32), протекающую во фрактальном пространстве и требующую для своего описания эффективной спектральной размерности
/2 в пределах погрешности определения этих параметров. Таким образом, кинетические кривые автозамедленного типа представляют реакцию типа (4.32), протекающую во фрактальном пространстве и требующую для своего описания эффективной спектральной размерности ![]() [58]. Укажем, что переход от автоускоренного к автозамедленному режиму окисления происходит без изменения типа реакции, а единственно в силу изменения типа пространства - от евклидова к фрактальному. Поскольку для евклидова пространства ds = Df = d [59], то это означает изменение связности пространства, характеризуемой величиной
[58]. Укажем, что переход от автоускоренного к автозамедленному режиму окисления происходит без изменения типа реакции, а единственно в силу изменения типа пространства - от евклидова к фрактальному. Поскольку для евклидова пространства ds = Df = d [59], то это означает изменение связности пространства, характеризуемой величиной ![]() (для евклидова пространства ds = 3, для фрактального
(для евклидова пространства ds = 3, для фрактального ![]() = 0,32 ¸ 1,04). Отметим, что при неизменном типе реакции количество свободных радикалов для автоускоренного режима окисления ПААСО в три раза превышает эту величину для автозамедленного режима [58].
= 0,32 ¸ 1,04). Отметим, что при неизменном типе реакции количество свободных радикалов для автоускоренного режима окисления ПААСО в три раза превышает эту величину для автозамедленного режима [58].
Рассмотрим условия реализации кинетических кривых автоускоренного и автозамедленного типов согласно полученным выше результатам. Граничным условием для указанного перехода является критерий х = 1 в соотношении (6.20): при x < 1 реализуется автозамедленный тип окисления, а при x > 1 - автоускоренный. При х = 1 получим линейную зависимость ![]() , также встречающуюся на практике [37]. Для реакции типа (4.32) в евклидовом пространстве характер кривой
, также встречающуюся на практике [37]. Для реакции типа (4.32) в евклидовом пространстве характер кривой ![]() определяется размерностью этого пространства: для d = 1 x < 1 (автозамедленный режим), для d = 2 х = 1 (линейная зависимость) и для d = 3 x > 1 (автоускоренный режим). Для реакции типа (4.34) в евклидовом пространстве с любой размерностью d £ 3 кинетические кривые будут представлять автозамедленный режим. Поскольку максимальные значения ds = 4/3 [23] и
определяется размерностью этого пространства: для d = 1 x < 1 (автозамедленный режим), для d = 2 х = 1 (линейная зависимость) и для d = 3 x > 1 (автоускоренный режим). Для реакции типа (4.34) в евклидовом пространстве с любой размерностью d £ 3 кинетические кривые будут представлять автозамедленный режим. Поскольку максимальные значения ds = 4/3 [23] и ![]() = 1,20 (уравнение (1.72) при Df = 3), то реакции во фрактальных пространствах всегда будут характеризоваться автозамедленным типом кинетических кривых. Последний вывод ожидался, поскольку кривые указанного типа характеризуются уменьшением скорости реакции k со временем t. Как отмечалось выше, фрактальные реакции, т.е., либо реакции фрактальных объектов, либо реакции во фрактальных пространствах, описываются соотношением (1.68) [20; 22].
= 1,20 (уравнение (1.72) при Df = 3), то реакции во фрактальных пространствах всегда будут характеризоваться автозамедленным типом кинетических кривых. Последний вывод ожидался, поскольку кривые указанного типа характеризуются уменьшением скорости реакции k со временем t. Как отмечалось выше, фрактальные реакции, т.е., либо реакции фрактальных объектов, либо реакции во фрактальных пространствах, описываются соотношением (1.68) [20; 22].
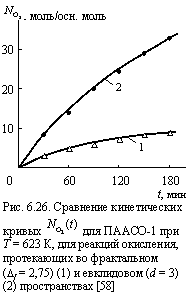
Изложенные выше результаты позволяют описание кинетических кривых ![]() с помощью простых степенных закономерностей. На рис. 6.24 приведено сравнение экспериментальных и теоретических кривых
с помощью простых степенных закономерностей. На рис. 6.24 приведено сравнение экспериментальных и теоретических кривых ![]() , рассчитанных согласно уравнениям [58]:
, рассчитанных согласно уравнениям [58]:
![]() (6.30)
(6.30)
для ПААСО-1 (автозамедленный тип кривой) и
![]() (6.31)
(6.31)
для ПААСО-4 (автоускоренный тип кривой).
Как можно видеть, уравнения (6.30) и (6.31) корректно описывают экспериментальные кинетические кривые ![]() обоих исследуемых типов.
обоих исследуемых типов.
Сравнение величин ![]() , определенных согласно уравнению (1.72), и ds, рассчитанных по уравнению (6.17), показало [61], что, как и следовало ожидать,
, определенных согласно уравнению (1.72), и ds, рассчитанных по уравнению (6.17), показало [61], что, как и следовало ожидать, ![]() £ ds. Это означает, что величины
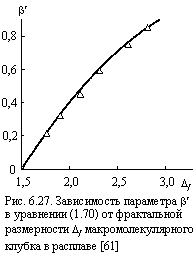
£ ds. Это означает, что величины ![]() и ds для полимерных расплавов подчиняются теореме о субординации, уравнению (1.70). Из сочетания уравнений (1.70), (1.72) и (6.17) можно оценить параметр b¢, характеризующий степень временного (энергетического) беспорядка [22]. Как оказалось, величина b¢ является функцией Df, увеличиваясь по мере роста Df (рис. 6.27). Из данных рис. 6.27 можно получить аналитическую взаимосвязь b¢ и Df [61]:
и ds для полимерных расплавов подчиняются теореме о субординации, уравнению (1.70). Из сочетания уравнений (1.70), (1.72) и (6.17) можно оценить параметр b¢, характеризующий степень временного (энергетического) беспорядка [22]. Как оказалось, величина b¢ является функцией Df, увеличиваясь по мере роста Df (рис. 6.27). Из данных рис. 6.27 можно получить аналитическую взаимосвязь b¢ и Df [61]:
b¢ = 0,72 (Df - 1,5)0,8. (6.32)
Как следует из уравнения (6.32), нижнее предельное значение b¢ = 0 достигается при Df = 1,5, т.е., для протекаемого клубка [14], в случае, когда и низкомолекулярные, и высокомолекулярные вещества могут свободно проходить через макромолекулярный клубок. В этом случае связность клубка уже не имеет значения. Максимальное значение b¢ = 1 (или условие = ds) достигается при Df = d, т.е., для евклидовых объектов, т.е., временной (энергетический) беспорядок является свойством только фрактальных объектов [61]. Исходя из уравнений (6.17) и (6.32), величину для фантомных фракталов можно определить так [61]:
![]() . (6.33)
. (6.33)
Таким образом, из уравнения (6.33) следует ![]() = 0 при Df = 1,5 и
= 0 при Df = 1,5 и ![]() = 1,2 при Df = d = 3.
= 1,2 при Df = d = 3.
Существует два основных типа скейлинговых соотношений: степенные или экспоненциальные функции [39; 40; 51-55]. Нанесение на график зависимостей ![]() , приведенных на рис. 6.24, в двойных логарифмических координатах показало, что кривые автозамедленного типа можно линеаризовать, а автоускоренного типа - нет. Точнее, для кривых
, приведенных на рис. 6.24, в двойных логарифмических координатах показало, что кривые автозамедленного типа можно линеаризовать, а автоускоренного типа - нет. Точнее, для кривых ![]() последнего из указанных типов линеаризация в рамках уравнения (6.30) возможна только для начального участка (см. рис. 6.24). Это означает, что для описания кинетических кривых автозамедленного типа требуется степенная функция, а для кривых автоускоренного типа - экспоненциальная.
последнего из указанных типов линеаризация в рамках уравнения (6.30) возможна только для начального участка (см. рис. 6.24). Это означает, что для описания кинетических кривых автозамедленного типа требуется степенная функция, а для кривых автоускоренного типа - экспоненциальная.

Линеаризация кривой ![]() автозамедленного типа для ПААСО-1 (рис. 6.24) дает следующее соотношение [61]:
автозамедленного типа для ПААСО-1 (рис. 6.24) дает следующее соотношение [61]:
![]() , (6.34)
, (6.34)
где показатель g = 0,70. Такое значение g исключает применение соотношений (6.25) и (6.26) для d = 3 в случае протекания деструкции в евклидовом пространстве. Согласно уравнению (6.33) величина ![]() для ПААСО-1 равна ~ 0,76 при Df = 2,45 [47]. Формально такая величина
для ПААСО-1 равна ~ 0,76 при Df = 2,45 [47]. Формально такая величина ![]() допускает применение соотношения (6.28) для описания деструкции ПААСО в автозамедленном режиме (см. уравнение (6.30)), но следует помнить, что это соотношение описывает реакцию типа (4.32), т.е., реакцию одинаковых молекул. Для рассматриваемого случая предполагается реакция кислородного радикала с радикалом макромолекулы. Поэтому наиболее вероятным вариантом скейлингового соотношения для описания кривых
допускает применение соотношения (6.28) для описания деструкции ПААСО в автозамедленном режиме (см. уравнение (6.30)), но следует помнить, что это соотношение описывает реакцию типа (4.32), т.е., реакцию одинаковых молекул. Для рассматриваемого случая предполагается реакция кислородного радикала с радикалом макромолекулы. Поэтому наиболее вероятным вариантом скейлингового соотношения для описания кривых ![]() автозамедленного типа является соотношение для реакции ловушка-частица, где ловушка неподвижна, а движется частица [40]. В этом случае корректно уравнение (6.34) при условии g = b¢. Расчет по уравнению (6.32) дает b¢ = 0,69, что близко к приведенной выше величине g. Показанная на рис. 6.28 зависимость
автозамедленного типа является соотношение для реакции ловушка-частица, где ловушка неподвижна, а движется частица [40]. В этом случае корректно уравнение (6.34) при условии g = b¢. Расчет по уравнению (6.32) дает b¢ = 0,69, что близко к приведенной выше величине g. Показанная на рис. 6.28 зависимость ![]() от t-b¢ линейна, что дает возможность окончательно определить тип реакции следующим образом. Это реакция частица (Р) - ловушка (Т) (обозначения работы [40]), где подвижные частицы Р идентифицируются как молекулы кислорода (или микрорадикалы [3]), а неподвижные ловушки Т - как макромолекулярные клубки (или макрорадикалы [3]). Реакция протекает во фрактальном пространстве (величина b¢ определяется значением Df). В данном случае под фрактальным пространством понимается фрактальная структура макромолекулярного клубка [61].
от t-b¢ линейна, что дает возможность окончательно определить тип реакции следующим образом. Это реакция частица (Р) - ловушка (Т) (обозначения работы [40]), где подвижные частицы Р идентифицируются как молекулы кислорода (или микрорадикалы [3]), а неподвижные ловушки Т - как макромолекулярные клубки (или макрорадикалы [3]). Реакция протекает во фрактальном пространстве (величина b¢ определяется значением Df). В данном случае под фрактальным пространством понимается фрактальная структура макромолекулярного клубка [61].
Кривые ![]() автоускоренного типа для ПААСО-4 описываются экспоненциальными скейлинговыми соотношениями (6.12), (6.13) или следующим соотношением, полученным в работе [52] для реакций рекомбинации:
автоускоренного типа для ПААСО-4 описываются экспоненциальными скейлинговыми соотношениями (6.12), (6.13) или следующим соотношением, полученным в работе [52] для реакций рекомбинации:
с(t) ~ exp(-ta), (6.35)
где показатель a зависит от d как [52]:
![]() (6.36)
(6.36)
для свободной диффузии реагирующих частиц и
![]() (6.37)
(6.37)
для несвободной (принудительной) диффузии этих частиц.
Использование соотношений (6.12), (6.13) и (6.18) не позволило линеаризовать зависимости ![]() от t для ПААСО-4, но такую возможность дает соотношение (6.35) при a = 1 (рис. 6.29). Это означает, что кривые
от t для ПААСО-4, но такую возможность дает соотношение (6.35) при a = 1 (рис. 6.29). Это означает, что кривые ![]() автоускоренного типа описывают реакцию рекомбинации низкомолекулярных радикалов А· и В· [52]:
автоускоренного типа описывают реакцию рекомбинации низкомолекулярных радикалов А· и В· [52]:
A· + B· → инертные продукты. (6.38)

Таким образом, применимость того или иного скейлингового соотношения позволяет оценить общие особенности химических реакций в процессе термоокислительной деструкции полимерных расплавов.
Как указано выше, уравнение (6.17) корректно для фантомного пространства. Очевидно, такое фрактальное пространство может создавать траектория блуждания низкомолекулярных частиц (молекул кислорода, радикалов), которая может пересекать саму себя неограниченное число раз. При такой трактовке величина d в уравнении (6.13) может принимать любые значения. Авторы [62] выяснили структурные особенности термоокислительной деструкции поликарбоната на основе бисфенола А с помощью скейлингового подхода, в частности уравнения (6.13).
Образцы ПК в виде пленок получены поливом 5 %-х растворов полимера в хлороформе и тетрагидрофуране на горизонтальную целлофановую подложку. Это позволило получить образцы с одинаковым химическим строением, но разной структурой (величины Df для них равны 2,54 и 2,69, соответственно). Тепловое старение ПК выполнено в течение 12 час. при Тст = 510 К, т.е., при Тст > tll. Через каждые 1,5 часа пленки вынимали и измеряли их приведенную вязкость hпр. Далее согласно уравнению Шульца-Блашке [63] по значениям hпр определяли характеристическую вязкость [h], а по ее значениям согласно уравнению Марка-Куна-Хаувинка [64] рассчитывали средневязкостную молекулярную массу ![]() . Затем определяли число разрывов s на исходную макромолекулу по формуле [3]:
. Затем определяли число разрывов s на исходную макромолекулу по формуле [3]:
![]() , (6.39)
, (6.39)
где М0 и Мt - молекулярная масса полимера до и после деструкции, соответственно.

Для анализа кривых s(tст) в рамках скейлингового соотношения (6.13) требуется определить параметр с(t). Величина с рассматривается как число «выживших» в процессе реакции частиц [40; 52-55; 62]. В случае термоокислительной деструкции этот параметр следует рассматривать как число мест макромолекул, не подвергшихся разрыву в процессе деструкции. Тогда можно записать [62]:
c = sпр - s, (6.40)
где sпр - предельное число разрывов на одну макромолекулу.
Величину sпр можно определить разными способами. В работе [62] постулируется, что sпр достигается в том случае, когда окисляющийся ПК теряет свои полимерные свойства. Как известно [66], это происходит в случае снижения молекулярной массы полимера до величины М0 при которой в полимере уже не может формироваться сетка макромолекулярных зацеплений. Величина М0 определяется так [66]:
М0 » 2М3, (6.41)
где М3 - молекулярная масса участка цепи между узлами зацеплений, равная для ПК ~ 1780 [66].

Dп = Df - 1. (6.42)
Как следует из данных рис. 6.31, на начальном участке окисления (время деструкции tст £ 6 час.) зависимость ln(sпр - s) от tx, cоответствующая соотношению (6.13), линеаризуется при х=Dп/Dп+2»0,46, а при tст > 6 час - при х = d/d + 2 = 0,6. Это означает, что на начальном участке кривой s(tст), показанной на рис. 6.30, происходит окисление поверхности макромолекулярного клубка, вследствие чего образуются подвижные низкомолекулярные радикалы (см. схемы 6.15 и 6.16), а затем реакция окисления протекает в евклидовом пространстве c d = 3. Отметим, что в обоих случаях окисление протекает в среде с большими флуктуациями плотности [40] и скорость реакции в евклидовом пространстве намного выше, чем во фрактальном (рис. 6.30).

Для пленок ПК, полученных из раствора в хлороформе аналогичные зависимости для участка ускорения окисления (tст < 6 час) приведены на рис. 6.32. Из данных этого рисунка следует, что зависимость ln(sпр - s) от
Следовательно, результаты скейлингового анализа термоокислительной деструкции ПК с разной структурой показали, что начальные участки кинетических кривых окисления автоускоренного и s-образного типов описывают протекание окисление в идентичных условиях - во фрактальном пространстве с размерностью, равной размерности поверхности макромолекулярного клубка. Дальнейший ход кинетической кривой определяется типом пространства, в котором протекает окисление: переход в евклидово пространство дает резкое (практически линейное) ускорение окисления, а переход во фрактальное пространство с размерностью, равной фрактальной размерности макромолекулярного клубка - резкое замедление окисления. Рассмотренные примеры демонстрируют сильное влияние типа пространства, в котором протекает окисление полимера, на процесс его термоокислительной деструкции [62].
