Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

6.5. Взаимосвязь структуры и химических механизмов окисления полимерных расплавов

Частично взаимосвязь структуры и химических механизмов термоокислительной деструкции на примере расплавов ПАр и ПААСО была рассмотрена в разделе 6.4. В настоящем разделе этот вопрос будет исследован более детально [74].

На рис. 6.49 приведены кинетические кривые  для полученных разными методами поликонденсации ПААСО (см. табл. 6.1) при Т_ст = 623К [74]. Как отмечалось выше, для ПААСО-1 и ПААСО-2 окисление протекает в автозамедленном режиме, а для ПААСО-3 и ПААСО-4 - в автоускоренном. По аналогии с термоокислительной деструкцией другого гетероцепного полиэфира ПК можно предположить следующую простую схему этого процесса [37]:

(зарождение цепи),    (6.56)

(продолжение цепи),             (6.57)

(обрыв цепи),        (6.58)

(обрыв цепи)                      (6.59)

На рис. 6.50 и 6.51 приведены кривые выхода основных газообразных продуктов деструкции ПААСО (окиси и двуокиси углерода) при Т_ст = 623К. Из этих рисунков следует, что основным продуктом является СО, поскольку его концентрация примерно в 20 раз выше, чем концентрация СО₂. Как показано для ПК [37], СО образуется исключительно в результате окисления метильных групп, СО₂ - как при распаде сложноэфирных связей, так и при окислении метильных групп. Эти наблюдения позволяют предположить, что при окислении ПААСО основным радикалом будет СН₂^· и тогда схему (6.56) ¸ (6.59) можно в простейшем виде конкретизировать так [74]:

- CH₂H + O₂ → CH₂^· + HO₂^·(зарождение цепи),          (6.60)

- СH₂^· + O₂ → - CH₂O^· (продолжение цепи),               (6.61)

- СH₂O₂^· + - CH₂O₂^· → 2CO + 2HO₂ (обрыв цепи),     (6.62)

- CH₂^· + - CH₂O₂^· → 2CO + 2H₂ (обрыв цепи)             (6.63)

Реакция продолжения цепи (6.51) была исключена из рассмотрения по двум следующим причинам. Во-первых, при T > 523К бимолекулярная реакция образования гидроперекиси маловероятна [37]. Во-вторых, ни разрушение гидропероксидных групп, ни термический распад гидропероксида согласно приведенным схемам не дает тех основных газообразных продуктов деструкции, которые были обнаружены экспериментально (рис. 6.50 и 6.51).

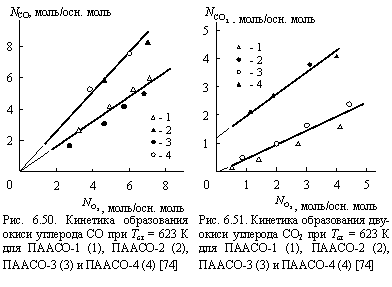
На рис. 6.52 приведены зависимости выхода СО (N_CO) и СО₂  от  для обоих режимов окисления (автозамедленного для ПААСО-1 и ПААСО-2, автоускоренного для ПААСО-3 и ПААСО-4). В обоих случаях наблюдаются линейные корреляции, проходящие через начало координат. Это означает, что при образовании СО в процессе окисления метильных групп, принимает участие кислород воздуха. Теоретическое соотношение (в молях) СО:О₂=2:1, тогда как из графиков рис. 6.52 получим 2 : 2,6 для автозамедленного режима и 2 : 4,2 - для автоускоренного. Очевидно, избыток кислорода, как и в случае ПК [37], связывается полимером. Кроме того, образующаяся согласно схеме (6.62) вода может приводить к гидролитическому распаду сложноэфирных связей [37].

Проницаемость макромолекулярного клубка для кислорода можно оценить степенью его компактности - чем компактнее клубок, тем меньше кислорода может проникнуть в него за единицу времени. В свою очередь, степень компактности клубка количественно можно охарактеризовать его плотностью r, оцениваемой согласно соотношению (2.22), где в качестве коэффициента пропорциональности принята плотность полимера в случае его плотной упаковки r_пл, которую можно принять равной плотности его кристаллической фазы (для ПААСО r_пл = 1,4 ´ 10³ кг/м³ [73]). На рис. 6.53 приведена зависимость  от r^-1 для ПААСО при трех температурах испытаний (623, 673 и 723 К). Как можно видеть, эта зависимость хорошо аппроксимируется линейной корреляцией, которую аналитически можно выразить так [74]:

 = 0,55(r^-1 - 1,4)                                       (6.64)

Такое соотношение позволяет предположить, что для макромолекулярных клубков в расплаве коэффициент диффузии по кислороду  пропорционален r^-1. Далее, константа скорости окисления k_d и  связаны следующим соотношением [2]:

.                          (6.65)

Полагая, что при средней величине r^-1 » 15 (рис. 6.53) величина » 5 ´ 10^-5 см²/с, можно рассчитать значение k_d для обоих типов кривых - с автоускорением и автозамедлением. Оказалось, что для первых величина k_d примерно в 4 раза меньше, чем для вторых. Затем можно использовать следующее соотношение [3]:

,                                  (6.66)

где  - концентрация радикалов СН₂О₂^·, [RH] - концентрация мономерных звеньев полимера.

Определив величину  по данным рис. 6.49, можно рассчитать величину   для обоих указанных случаев. Оказалось, что концентрация RO₂^· более чем в три раза выше в автоускоренном режиме, чем автозамедленном. Резюмируя все сказанное выше, можно предположить, что в случае ПААСО режимы автоускорения (ПААСО-3 и ПААСО-4) и автозамедления (ПААСО-1 и ПААСО-2) различаются химическим механизмом на стадии обрыва цепи: для первого случая справедлива схема (6.58), для второго - схема (6.59). Этот вывод обусловлен следующими причинами.

• 1) согласно реакции (6.62), выход СО на моль О₂ существенно ниже, чем в реакции (6.63). Аналогичное соотношение наблюдается для кривых автоускоренного режима по сравнению с автозамедленным (рис. 6.52);
• 2) гораздо более высокая концентрация радикалов RO₂ (или СН₂О₂) предполагает высокую вероятность автокаталической реакции между ними [2; 3].
• 3) 3) наличие Н₂О в реакции (6.62) предполагает гидролитический распад сложноэфирных связей, что также должно привести к ускорению реакции.

Кроме того, как отмечалось выше, автоускоренный режим типичен для более низких температур, автозамедленный - для более высоких. Рассмотрим вопрос эквивалентности изменений температуры теплового старения и структуры (своего рода принцип температурно-структурной суперпозиции). Авторы [74] не располагали температурной зависимостью  для ПААСО и поэтому использовали известный факт [2], что энергия активации микродиффузии О₂ составляет величину ~ 20 ¸ 40 кДж/моль. Тогда можно записать по аналогии с полиэтиленом [2]:

cм²/с.            (6.67)

Простые оценки согласно уравнению (6.67) показали, что если принять при Т_ст = 373К  = 5 ´ 10^-5 см²/с [2], то увеличение  в четыре раза эквивалентно росту Т_ст до 428К, т.е., на 55 К. Иначе говоря, изменение структуры макромолекулярного клубка, характеризуемое уменьшением фрактальной размерности D_f от 2,90 до 2,60, эквивалентно повышению температуры на 55 К, что само по себе способно изменить режим окисления от автоускоренного к автозамедленному [4].

Еще одним возможным химическим механизмом, ответственным за автоускорение при термоокислительной деструкции ПААСО, является окисление альдегидных групп, образующихся из метильных групп согласно схемам (6.15) и (6.16). Отметим, что этот вариант совпадает с предложенной выше реакцией (6.56) и имеет те же продукты окисления (СО и НО₂^·).

Наиболее же общей схемой перехода от автоускоренного к автозамедленному режиму является анализ разветвленных цепных реакцией в виде обобщающей формулы [3]:

,                         (6.68)

где j - фактор самоускорения цепной вырожденно-разветвлен-ной реакции; n_к - длина кинетической цепи; d - вероятность вырожденного разветвления цепи; q - время жизни разветвленного продукта.

В свою очередь, величина d определяется как произведение [3]:

d = as,                                                                 (6.69)

где a - вероятность образования разветвленного продукта в одном звене цепи; s - средний выход свободных радикалов при распаде этого продукта.

Согласно уравнению (6.68), если j > 0, то процесс окисления будет протекать с самоускорением, при j < 0 скорость процесса будет ограничена, после какого-то времени концентрация разветвляющегося продукта достигнет некоторого предельного значения, т.е., процесс окисления будет протекать автозамедленно. Из уравнения (6.68) нетрудно видеть, что определяющим фактором для такого перехода является величина d. Уменьшение d приведет к реализации условия j < 0 (при n_кd < 1) и процесс окисления будет протекать с автозамедлением. В свою очередь, из уравнения (6.69) следует, что основной вклад в вариацию d вносит параметр s, который может изменяться в широких пределах - от 10^-4 до 1 [3]. Малые значения s обусловлены гибелью первичных радикалов в результате внутриклеточной рекомбинации [3]. В рамках клеточной модели скорость этого процесса k_р связана с коэффициентом диффузии D следующим образом [1]:

k_p = 4pN_ADl,                                                       (6.70)

где N_A - число Авогадро; l - длина диффузионного скачка.

Таким образом, из сказанного выше вытекает следующая тенденция. Повышение степени компактности макромолекулярного клубка в расплаве, характеризуемое ростом D_f, определяет снижение коэффициента диффузии, что приводит к снижению скорости рекомбинации радикалов, увеличению s и росту j. При достижении критерия j = 0 тип кинетических кривых  изменяется от автозамедленного к автоускоренному [74].

Следовательно, изложенные выше результаты продемонстрировали возможность влияния структуры полимерного расплава не только на количественные характеристики процесса термоокислительной деструкции, но и качественные изменения в этом процессе, в частности, химический механизм реакции. Увеличение фрактальной размерности макромолекулярного клубка означает повышение степени его компактности, снижение коэффициента диффузии, что эквивалентно понижению температуры теплового старения. Указанные факторы могут вызвать переход от автозамедленного режима окисления к автоускоренному и наоборот. Основным фактором в этом случае является ослабление диффузии в полимерном расплаве, определяющее снижение скорости рекомбинации радикалов при вырожденном разветвлении цепи.

В рамках формальной кинетики химических реакций простая бимолекулярная реакция типа (4.32) описывается следующим уравнение [3]:

,                                             (6.71)

где [A] - концентрация реагирующего вещества, k₂ - константа скорости реакции, а показатель 2 означает второй кинетический порядок реакции.

Недостатки такого формального подхода к кинетике химических реакций очевидны. По существу, используемые параметры никак не связаны со структурой реагирующих веществ и это обстоятельство определяет тот факт, что k₂ может быть в лучшем случае параметром сравнения аналогичных реакций. Подробнее уравнение (6.71) будет проанализировано ниже.

Указанный недостаток частично устранен во фрактальной модели кинетики химических реакций [20; 22; 35; 51-55]. Однако в указанной трактовке также отсутствует четкая идентификация структуры полимера, в которой протекает реакция. Тем не менее, использование фрактальной кинетики дает возможность аналитически описать взаимосвязь структурных (или физических) параметров и классических химических ее характеристик (например, порядок реакции и константа скорости реакции). Авторы работы [75] установили такую аналитическую взаимосвязь на примере термоокислительной деструкции ПААСО при двух температурах теплового старения (623 и 723К).

Прежде чем выполнить получение указанной взаимосвязи, необходимо убедиться, что кинетика термоокислительной деструкции, описываемая кинетическими кривыми , действительно представляет бимолекулярную реакцию. Как показано авторами работы [55], в этом случае спад концентрации реагирующего вещества в логарифмических координатах должен быть функцией t в степени 0,250 (для случайных блужданий) или 0,125 (для случайных блужданий с непрерывным временем). Количество кислорода , необходимое для окисления всех алифатических и ароматических групп ПААСО, равно ~ 24,1 моль О₂/осн. моль ПААСО. Отметим, что величина   определяется химическим строением полимера. Как и ранее, концентрация непрореагировавшего вещества определяется как разность . На рис. 6.54 показана зависимость   от продолжительности реакции t в двойных логарифмических координатах для ПААСО-1 (см. табл. 6.1) при двух температурах теплового старения (т_ст = 623 и 723 К). Как можно видеть, спад концентрации непрореагировавшего вещества в указанных координатах описывается линейной зависимостью, из наклона которой был определен показатель для t, равный ~ 0,145, т.е., исследуемая реакция может рассматриваться как бимолекулярная, а траектория молекул оксиданта на структуре расплава ПААСО - как случайное блуждание с непрерывным временем (СБНВ) [55].

Как показано в работе [3], построение зависимостей ln  от t дает линейную зависимость для реакции первого порядка и криволинейные зависимости - для реакций более высоких порядков. При этом, чем выше порядок реакции, тем медленнее спад ln  со временем. На рис. 6.55 приведены такие зависимости для ПААСО при указанных выше температурах теплового старения (кривая для ПААСО при Т_ст = 723К смещена по оси ординат до совмещения начальных точек кривых при t = 0). Как можно видеть, скорость спада ln  со временем различается для двух указанных температур - при Т_ст = 723К спад заметно медленнее. Это означает разный порядок термоокислительной деструкции ПААСО при указанных температурах, причем повышение Т_ст увеличивает порядок реакции [75].

Как известно [20; 22], в случае протекания реакции во фрактальном пространстве наблюдается снижение ее скорости k со временем t, что аналитически выражается соотношением (1.68), где показатель h связан с эффективной спектральной размерностью   уравнением (1.69). Размерность   является основным структурным фактором, контролирующим процесс термоокислительной деструкции расплавов гетероцепных полиэфиров [38]. Взаимосвязь размерностей   и D_f дается уравнением (1.72).

Уравнение фрактальной кинетики для описания кривой  имеет вид [35]:

,                              (6.72)

где порядок реакции n связан с эффективной спектральной размерностью   следующим уравнением [35]:

.                                                          (6.73)

Как показали оценки   согласно уравнению (1.72), для ПААСО-1 при Т_ст = 623К  = 0,88, при Т_ст = 723К  = 0,56. Соответственно, из уравнения (1.69) величины h равны 0,56 и 0,72. Тогда порядок реакции n при Т_ст = 623К равен 3,27 и при Т_ст = 723К - n = 4,57. Таким образом, фрактальность структуры приводит к тому, что увеличение Т_ст и соответствующее уменьшение D_f увеличивает порядок реакции n. Следовательно, сочетание уравнений (1.69), (1.72) и (6.73) дает аналитическое соотношение между физическим (структурным) параметром D_f и химической характеристикой термоокислительной деструкции n [75].

Поскольку левую часть уравнения (6.72) можно записать как t^-h, (см. уравнение (1.68)), то с учетом такой замены согласно этому уравнению авторы [75] рассчитали величины k_d в рамках фрактальной кинетики, которые оказались равны 0,566´10^-6 и 0,70´10^-8 с^-1 для Т_ст = 623 и 723 К соответственно. Отметим важный момент: для более высокой температуры величина k_d почти на два порядка меньше, чем для более низкой. На первый взгляд, это представляется ошибочным результатом, тем более, что полученные обычным методом (построением анаморфоз) величины k_d равны 0,19´10^-4 и 0,82´10^-4 с^-1 для Т_ст = 623 и 723 К соответственно. Однако, в рамках фрактальной кинетики величина k_d определяется эффективной связностью структуры, т. е. величиной . Уменьшение   по мере роста Т_ст приводит к снижению k_d. Более низкие значения k_d во фрактальном пространстве показывают обязательное снижение скорости реакции по сравнению с евклидовым пространством.

В рамках фрактального анализа достаточно просто выяснить аналитическую взаимосвязь между k_d и . Как отмечалось выше, траекторию молекулы (атома) кислорода на структуре полимера можно описать СБНВ. Число мест на структуре полимера  (S) (число реакционноспособных центров макромолекул), посещенных СБНВ, как функция времени дается так [76]:

.                                                          (6.74)

можно предположить, что величина k_d будет тем выше, чем больше реакционноспособных центров смогут посетить молекулы (атомы) кислорода: k_d ~ (S). Тогда [75]:

.                                               (6.75)

Как показали оценки, между lnk_d и   действительно наблюдается корреляция, линеализировать которую можно, используя функциональную зависимость lnk_d[( )^1/2], которая показана на рис. 6.56. из графика этого рисунка можно получить [75]:

- lnk_d = 30 - 14( )^1/2.                                      (6.76)

Как следует из данных рис. 6.56 и уравнения (6.76), при  = 0 и lnk_d = -30 и k_d » 10^-13 с^-1, что с практической точки зрения означает нулевую величину k_d (точнее, k_d → 0). [75].

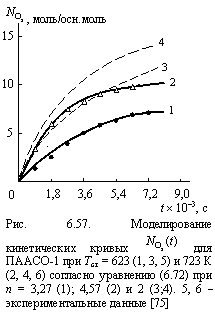
На рис. 6.57 приведено моделирование кинетических кривых  для ПААСО-1 при Т_ст = 623 и 723 К согласно уравнению (6.72). Использование указанных выше величин n и k_d для фрактального пространства дает хорошее соответствие с экспериментом, тогда как использование n = 2 и величин k_d для евклидова пространства дает более быстрый рост  со временем, чем наблюдается экспериментально. Это обстоятельство еще раз подтверждает, что уменьшение скорости поглощения кислорода во фрактальных пространствах по сравнению с евклидовым является характерным свойством кинетики термоокислительной деструкции [75].

Далее рассмотрим вопрос о корректности уравнения (6.71) с точки зрения фрактального анализа. Как следует из уравнений (5.18) и (6.73), второй порядок реакции достигается только при h = 0 или  = 2,0, т. е. только в случае протекания в евклидовом пространстве. Однако, как следует из соотношения (1.68), в этом случае k_d = d[A]/dt = const. Далее возможны два варианта. В первом из них при условии d[A]/dt = const и k₂ = const величина [A] также постоянна, иначе говоря, реакция не идет. Во втором случае d[A]/dt = const и для реализации реакции величина k₂ должна быть переменной: k₂ ~ 1/[A]². В этом случае само определение k₂ как константы скорости реакции теряет свой смысл. Указанные несоответствия являются следствием формального вывода уравнения (6.71). более подробный анализ поведения константы скорости реакции во фрактальных и евклидовых пространствах дан в разделе 6.1 [36].

Таким образом, приведенные выше данные демонстрируют, что для одного и того же полимера (при = const) химические характеристики термоокислительной деструкции полимера (n и k_d) полностью определяются структурой полимерного расплава, характеризуемой размерностью D_f. константа скорости деструкции определяется степенью связности макромолекулярного клубка, характеризуемой эффективной спектральной размерностью. Показана некорректность уравнений формальной кинетики в рамках фрактального анализа [75].