
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.1. Структурный критерий изменения типа кинетических кривых
Как отмечалось в предыдущей главе, существует два основных типа кинетических кривых окисления полимеров: кривые автоускоренного типа с четко выраженным периодом индукции и кривые, экспоненциально убывающие во времени (автозамедленного типа). Также предполагается [1], что s-образные кинетические кривые по своей физической сущности являются сочетанием двух первых типов. Эммануэль полагал [1], что тип кинетической кривой определяется химическим строением полимера и температурой испытаний. Так, кривые автоускоренного типа характерны для полимеров, содержащих связи С-Н, при температурах ниже ~ 473 К, а кривые автозамедленного типа - для окисления различных карбо- и гетероцепных полимеров при температурах выше 473 К. Однако, из изложенного в предыдущей главе материала очевидно, что авторы [2], совершенно верно определив роль структуры в стабилизации твердофазных полимеров, недооценили эту роль для случая полимерных расплавов. Исходя из вышеизложенного, авторы работ [3-7] преследовали три цели. Во-первых, было показано, что переход кинетических кривых при термоокислительной деструкции полимеров от автоускоренного к автозамедленному режиму окисления лимитируется физической структурой полимера. Во-вторых, было получено аналитическое условие этого перехода в рамках фрактального анализа. И, наконец, было продемонстрировано, что тип кинетической кривой определяется видом пространства (фрактальное или евклидово), в котором протекает реакция термоокислительной деструкции. Рассмотрим эти вопросы более подробно.
На рис. 6.49 и 7.1 приведены временные зависимости количества поглощенного кислорода ![]() и числа разрывов на исходную макромолекулу s(t), характеризующие кинетику термоокислительной деструкции для ПААСО (см. табл. 6.1) и ПК (табл. 7.1), соответственно. Как можно видеть, в обоих случаях реализуется переход от автозамедленного (или S-образного) режима к автоускоренному при одинаковой температуре теплового старения и неизменном химическом строении полимера. Сравнение данных рис. 6.49 и 7.1, с одной стороны, и табл. 6.1 и 7.1, с другой, показывает, что этот переход ассоциируется с увеличением фрактальной размерности Df макромолекулярного клубка в расплаве, что предполагает его чисто структурную природу [3]. Рост Df означает увеличение компактности макромолекулярного клубка [8] и, следовательно, ослабление диффузии кислорода в его внутренние области (см. раздел 6.5). При определенном значении Df (Df = 2,54 ¸ 2,69 для ПК и 2,72 ¸ 2,84 для ПААСО) происходит изменение типа кинетической кривой и, следовательно, химического механизма окисления полимера [9; 10]. Исходя из скейлингового анализа, выполненного в работе [11] (подробно см. раздел 6.2), можно предположить, что наблюдаемое изменение типа кинетической кривой происходит в том случае, когда число реакционноспособных мест макромолекулы на поверхности клубка Nпов и в его объеме Nоб становится равным [6]:
и числа разрывов на исходную макромолекулу s(t), характеризующие кинетику термоокислительной деструкции для ПААСО (см. табл. 6.1) и ПК (табл. 7.1), соответственно. Как можно видеть, в обоих случаях реализуется переход от автозамедленного (или S-образного) режима к автоускоренному при одинаковой температуре теплового старения и неизменном химическом строении полимера. Сравнение данных рис. 6.49 и 7.1, с одной стороны, и табл. 6.1 и 7.1, с другой, показывает, что этот переход ассоциируется с увеличением фрактальной размерности Df макромолекулярного клубка в расплаве, что предполагает его чисто структурную природу [3]. Рост Df означает увеличение компактности макромолекулярного клубка [8] и, следовательно, ослабление диффузии кислорода в его внутренние области (см. раздел 6.5). При определенном значении Df (Df = 2,54 ¸ 2,69 для ПК и 2,72 ¸ 2,84 для ПААСО) происходит изменение типа кинетической кривой и, следовательно, химического механизма окисления полимера [9; 10]. Исходя из скейлингового анализа, выполненного в работе [11] (подробно см. раздел 6.2), можно предположить, что наблюдаемое изменение типа кинетической кривой происходит в том случае, когда число реакционноспособных мест макромолекулы на поверхности клубка Nпов и в его объеме Nоб становится равным [6]:
Nпов = Nоб. (7.1)
Таблица 7.1
Фрактальная размерность Df макромолекулярного клубка для образцов ПК, полученных из разных растворителей [7]
|
Растворитель |
Df |
|
Хлористый метилен |
2,45 |
|
Хлороформ |
2,54 |
|
Тетрагидрофуран |
2,69 |
|
1,4-диоксан |
2,74 |
Ранее было показано, что доля макромолекулярного клубка bd, распадающаяся в процессе деструкции, зависит от Df и определяется уравнением (6.3). Следовательно, реальную величину числа реакционноспособных мест Nоб в объеме макромолекулярного клубка можно записать так [3]:
Nоб = NМ(3 - Df) - Nпов, (7.2)
где NМ - число реакционноспособных мест на макромолекулу при условии их полной доступности. Очевидно, величина NМ определяется химическим строением полимера.
Cоотношение параметров Nоб и Nпов контролируется соотношением объема Vфр и поверхности Sфр фрактального объекта, которое равно [12]:
![]() , (7.3)
, (7.3)
где R - радиус фрактального объекта, в нашем случае равный радиусу инерции Rg макромолекулярного клубка.

![]() (7.4)
(7.4)
и для ПК в хлороформе [13]:
![]() (7,5)
(7,5)
где ![]() и Mh - средневесовая и средневязкостная молекулярные массы соответственно. В уравнениях (7.4) и (7.5) величины Rg получены в нм.
и Mh - средневесовая и средневязкостная молекулярные массы соответственно. В уравнениях (7.4) и (7.5) величины Rg получены в нм.
Сочетание уравнений (7.1) ¸ (7.5) позволяет получить структурный критерий перехода кинетических кривых окисления от автозамедленного (S-образного) режима к автоускоренному [3-7]:
![]() , (7.6)
, (7.6)
где ![]() - критическое значение Df при указанном переходе; d - размерность евклидова пространства, в котором рассматривается фрактал, а Rg также дается в нм.
- критическое значение Df при указанном переходе; d - размерность евклидова пространства, в котором рассматривается фрактал, а Rg также дается в нм.
Отметим две важные особенности уравнений (7.6). Во-первых, в этом уравнении отсутствует параметр NМ, т.е., величина ![]() не зависит от химического строения полимера. Во-вторых, увеличение Rg приводит к повышению
не зависит от химического строения полимера. Во-вторых, увеличение Rg приводит к повышению ![]() . Это полностью согласуется с предположением, послужившим основой для вывода уравнения (7.6): величина Nоб растет пропорционально кубу Rg, а Nпов - квадрату Rg, т.е., увеличение Rg приводит к повышению отношения Vфр/Sфр.
. Это полностью согласуется с предположением, послужившим основой для вывода уравнения (7.6): величина Nоб растет пропорционально кубу Rg, а Nпов - квадрату Rg, т.е., увеличение Rg приводит к повышению отношения Vфр/Sфр.
Рассмотрим граничные условия для уравнения (7.6). Для Df = 0, т.е., для точечного объекта, Rg = 0 и критерий (7.6) справедлив для нуль-мерного объекта. Для Df = d = 3 Rg ® ¥ или, как и следовало ожидать, для евклидова объекта масштаб измерения не имеет значения [6].
Рассчитанные по уравнению (7.6) с использованием соотношений (7.4) и (7.5) величины ![]() оказались равны 2,76 для ПК и 2,78 - для ПААСО, что превосходно согласуется с указанным выше экспериментальным интервалом Df для перехода [3].
оказались равны 2,76 для ПК и 2,78 - для ПААСО, что превосходно согласуется с указанным выше экспериментальным интервалом Df для перехода [3].
Рассмотрим влияние структуры макромолекулярного клубка на режим автоускорения термоокислительной деструкции. Как было показано в работе [13], продуктом, ответственным за автоускоренный режим кинетических кривых, могут быть альдегидные группы, образующиеся из метильных групп (которые присутствуют в ПААСО и ПК) по схеме (6.15). В свою очередь, окисление альдегидных групп, протекающее по схеме (6.16), приводит к образованию активных свободных радикалов R· и низкомолекулярных радикалов НО2·. Последние являются подвижными радикалами, что позволяет рассматривать их как случайные блуждания и использовать для их описания реакцию типа (4.32) [14; 15]. Стандартная классическая реакция второго порядка описывается соотношением [16]:
![]() , (7.7)
, (7.7)
где rСБ - плотность случайных блужданий.
Для микроскопически гетерогенных (фрактальных) сред соотношение (7.7) видоизменяется следующим образом [16]:
![]() , (7.8)
, (7.8)
а интегрирование соотношения для скорости реакции можно записать так (с учетом квадратичной зависимости или s от t [1]) [7]:
![]() , (7.9)
, (7.9)
где rСБО - начальная плотность случайных блужданий, h - показатель неоднородности в соотношении (1.68) (0 < h < 1). Кроме того, показатель в соотношении (7.9) может быть определен согласно уравнению (1.69) как эффективная спектральная размерность ![]() среды, в которой протекает реакция [6].
среды, в которой протекает реакция [6].
Для момента времени t = 0 величина rСБО для ПК характеризуется предельным числом разрывов на исходную макромолекулу sпр (см. уравнения (6.39) и (6.41)). Величину rСБ, которая определяет плотность «выживших» случайных блужданий, характеризует разность (sпр - s) (см. уравнение (6.40)). Зависимости определенного таким образом параметра ![]() от времени 2t в двойных логарифмических координатах для ПК приведена на рис. 7.2. Как можно видеть, при малых t, соответствующих периоду индукции, зависимости линейны, имеют малый наклон, из которого можно определить величину 2(1 -h) = » 0,22 или h » 0,89. Эти величины и h соответствуют протеканию термоокислительной деструкции во фрактальном пространстве [16; 17]. В связи с этим следует отметить важный момент. Величина
от времени 2t в двойных логарифмических координатах для ПК приведена на рис. 7.2. Как можно видеть, при малых t, соответствующих периоду индукции, зависимости линейны, имеют малый наклон, из которого можно определить величину 2(1 -h) = » 0,22 или h » 0,89. Эти величины и h соответствуют протеканию термоокислительной деструкции во фрактальном пространстве [16; 17]. В связи с этим следует отметить важный момент. Величина ![]() связана с фрактальной размерностью макромолекулярного клубка Df уравнением (1.72). Согласно этому уравнению величина
связана с фрактальной размерностью макромолекулярного клубка Df уравнением (1.72). Согласно этому уравнению величина ![]() » 0,22 соответствует размерности Df » 1,78. Как следует из табл. 6.1 и 7.1, макромолекулярных клубков с такой размерностью для исследуемых полимеров не наблюдается. Однако, если предположить, что фрактальная размерность поверхности макромолекулярного клубка Dп определяется согласно уравнению (6.42), то можно получить еще одно подтверждение изложенного выше предположения о протекании реакции окисления на поверхности макромолекулярного клубка в случае кинетических кривых автоускоренного типа [11].
» 0,22 соответствует размерности Df » 1,78. Как следует из табл. 6.1 и 7.1, макромолекулярных клубков с такой размерностью для исследуемых полимеров не наблюдается. Однако, если предположить, что фрактальная размерность поверхности макромолекулярного клубка Dп определяется согласно уравнению (6.42), то можно получить еще одно подтверждение изложенного выше предположения о протекании реакции окисления на поверхности макромолекулярного клубка в случае кинетических кривых автоускоренного типа [11].
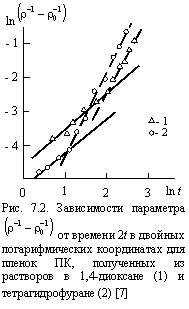
Далее на графиках рис. 7.2 наблюдается резкий переход к участку с гораздо более высоким наклоном, соответствующим ![]() » 2 или h » 0. Последнее означает протекание реакции окисления в евклидовом пространстве [17]. Таким образом, это подтверждает постулат, что скорость термоокислительной деструкции в значительной степени определяется типом пространства, в котором она протекает. Во фрактальном пространстве с малой связностью (
» 2 или h » 0. Последнее означает протекание реакции окисления в евклидовом пространстве [17]. Таким образом, это подтверждает постулат, что скорость термоокислительной деструкции в значительной степени определяется типом пространства, в котором она протекает. Во фрактальном пространстве с малой связностью ( ![]() » 0,22) скорость реакции невелика (период индукции). Повышение
» 0,22) скорость реакции невелика (период индукции). Повышение ![]() от ~ 0,22 до ~ 2,0 означает переход к евклидову пространству, что дает практически линейный участок кинетических кривых с постоянной и очень высокой скоростью окисления. Аналогичные результаты получены для кинетических кривых окисления ПААСО в автоускоренном режиме.
от ~ 0,22 до ~ 2,0 означает переход к евклидову пространству, что дает практически линейный участок кинетических кривых с постоянной и очень высокой скоростью окисления. Аналогичные результаты получены для кинетических кривых окисления ПААСО в автоускоренном режиме.
Данные рис. 7.2 согласуются с результатами компьютерного моделирования. Аргиракис и Копельман [18] показали, что эффективная спектральная размерность ![]() увеличивается со временем от ~ 1,3 до ~ 1,9 для двухмерного евклидова пространства и приближается к 2 гораздо быстрее для трехмерного евклидова пространства. Это обстоятельство обусловлено наличием в расплавах реальных полимеров кластеров (макромолекулярных клубков) разных размеров. Наличие кластеров малых размеров приводит к снижению
увеличивается со временем от ~ 1,3 до ~ 1,9 для двухмерного евклидова пространства и приближается к 2 гораздо быстрее для трехмерного евклидова пространства. Это обстоятельство обусловлено наличием в расплавах реальных полимеров кластеров (макромолекулярных клубков) разных размеров. Наличие кластеров малых размеров приводит к снижению ![]() , что учитывается введением разного рода коррекций. Однако, такие коррекции справедливы только для малых времен, а для достаточно больших t величина начинает расти, что и отражают графики рис. 7.2.
, что учитывается введением разного рода коррекций. Однако, такие коррекции справедливы только для малых времен, а для достаточно больших t величина начинает расти, что и отражают графики рис. 7.2.
Следовательно, изложенные выше результаты наглядно продемонстрировали, что переход кинетических кривых окисления полимеров от автозамедленного (s-образного) режима к автоускоренному определяется структурным фактором, а именно, достижением фрактальной размерностью макромолекулярного клубка критического значения, при котором количество реакционноспособных мест в объеме и на поверхности клубка становится одинаковым. В рамках фрактального анализа получено аналитическое соотношение, подтверждающее эту гипотезу. Переход от периода индукции к резкому ускорению термоокислительной деструкции в случае кинетических кривых автоускоренного типа обусловлен изменением типа пространства, в котором протекает реакция, от фрактального к евклидову [3-7].
