Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3. Уравнения квантовой механики с физическими переменными
Запишем уравнения движения квантовой механики в квазигидродинамическом виде. Как уже ранее было сказано, по-видимому, вначале их опубликовал Е. Маделунг в 1926 г. вслед за Э. Шредингером, а в 50-х годах Д. Бом [1,2].
Воспользуемся стандартным уравнением Шрёдингера для движения частицы массой m без спина и магнитного поля в произвольном потенциальном поле:
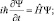
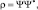(3.1)
которое является комплексным и, вообще говоря, эквивалентно двум уравнениям в действительном пространстве. Одно из этих уравнений приводится во многих учебниках по квантовой механике. Это уравнение обычно называют законом сохранения плотности вероятности
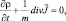(3.2)
где вектор плотности потока вероятности равен
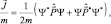(3.3)
где 
– оператор импульса. Для инфинитного движения в пространстве неограниченном хотя бы с одной стороны существует макроскопический импульс 
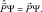
Тогда уравнение (3.1) можно записать в виде:
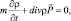(3.4)
Уравнение движения (3.4) получается умножением уравнения (3.1) и его комплексно сопряженного вида соответственно на Ψ и Ψ*, и вычитанием полученных уравнений. Следующее уравнение получается сложением названных выражений:
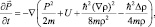(3.5)
Система уравнений (3.4), (3.5) с плотностью вероятности ρ(x, y, z, t) и импульсом 
является замкнутой и эквивалентной (3.1). Можно видеть, что это уравнение является квазигидродинамическим и нелинейным. Уравнение (3.5) записано несколько в другом виде, чем в [2, 3].
Если макроскопический импульс не существует, например, в области туннелирования, то систему уравнений (3.4), (3.5) необходимо записывать в других переменных. Она будет состоять из уравнения (3.2) и уравнения
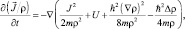(3.6)
Для движения квантовой системы из N невзаимодействующих частиц с макроскопическими импульсами и одинаковой массы имеем:
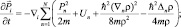(3.7)
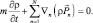(3.8)
С помощью уравнений (3.7) и (3.8) можно показать, что плотность вероятности для системы невзаимодействующих между собой частиц, как и прежде, равна произведению плотностей вероятности входящих в систему частиц.
Какова же роль квазигидродинамических квантовых уравнений движения? На наш взгляд, эти уравнения являются поверочными для принципа суперпозиции волновых функций. Квазигидродинамические уравнения детализирует принцип суперпозиции, делает его предметным, не допускает неограниченного суммирования квантовых состояний, например, как в случае волнового пакета. Для инфинитного движения квантовых частиц каждому виду энергии соответствует волновая функция.
Суперпозиция (сложение) волновых функций приводит не только к новому квантовому состоянию, но и приводит, как это можно видеть из смысла уравнений Шредингера для инфинитных состояний, к изменению энергии квантовой системы, о чем обычно не задумываются.
Обратимся вновь к уравнению (3.5). В стационарном случае оно будет иметь вид:
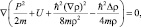(3.9)
или
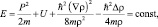(3.10)
где полная энергия квантовой частицы Е является аддитивной величиной, а квантовая составляющая энергии движения имеет вид:
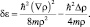(3.11)
Эту величины Д. Бом называл квантовым потенциалом. Далее можно будет убедиться, что наряду с величиной δε квантовая частица согласно гипотезе де Бройля обладает ещё собственной энергией движения пропорциональной её массе.
Литература
1. Вопросы причинности в квантовой механике. Сб. переводов под ред. Я.П. Терлецкого и А.А. Гусева. М.: ИЛ 1955. С. 34.
2. Ghosh S.K., Deb B.M. Densities, Density-Functionals and Electron Fluids. Physics Reports (Review Section of Physics Letters). 92 № 1 (1982).
3. Б.В. Алексеев, А.И. Абакумов. Об одном подходе к решению уравнения Шредингера Доклады Академии наук. Т. 262, С. 1100. 1982.