
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4. Движение квантовых частиц с нулевой массой покоя
В свое время Луи де Бройль весьма был озадачен тем, что уравнение Шредингера «покоится» на законах сохранения движения для квантов света и, тем не менее, не описывает волновые свойства фотонов [1]. При квазигидродинамическом описании такое возможно.
При квазигидродинамическом описании [2, 3] уравнения инфинитного движения квантовой частицы массы m в произвольном внешнем поле 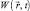 записываются в виде:
записываются в виде:
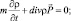 (4.1)
(4.1)
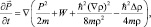 (4.2)
(4.2)
где 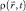 – пространственно-временное распределение плотности вероятности частицы;
– пространственно-временное распределение плотности вероятности частицы; 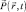 – макроскопический импульс частицы.
– макроскопический импульс частицы.
Поскольку первое уравнение приводится во многих учебниках по квантовой механике, а второе используется не часто, приведем краткую историю написания этой системы уравнений. Если ввести стандартные обозначения:
 (4.3)
(4.3)
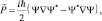 (4.4)
(4.4)
то, из уравнения Шредингера можно получить выписанную выше систему уравнений (4.1) и (4.2). Нелинейный метод описания движения квантовых частиц с помощью величин, имеющих физический смысл, использовался для численного решения квантовых задач. Например, при численных расчетах рассеяния квантовых частиц оказалось более удобным использовать квазигидродинамическое представление [3]. Однако численные расчеты не могут дать представления
о возможностях квазигидродинамического описания инфинитного движения квантовых частиц. Нам удалось найти ряд аналитических решений известных квантовых задач и понять, что описание инфинитного движения квантовых частиц с помощью волны плотности вероятности является менее противоречивым и более адекватным по сравнению с описанием с помощью волновой функции. И главное, квазигидродинамический подход позволяет предсказать ряд новых эффектов, которые по-новому объясняют известные прежние экспериментальные результаты и которые позволяют получить новые экспериментальные доказательства [5].
В исходной системе уравнений (4.1) и (4.2) введем макроскопическую скорость  из определения макроскопического импульса
из определения макроскопического импульса 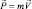 , тогда уравнение неразрывности в соответствии с формулой (4.1) можно записать в виде:
, тогда уравнение неразрывности в соответствии с формулой (4.1) можно записать в виде:
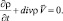 (4.5)
(4.5)
В этом случае уравнение неразрывности принимает стандартный вид и обычно называется дифференциальным законом сохранения плотности вероятности. Уравнение (4.2) при переходе от макроскопического импульса к макроскопической скорости запишется в виде:
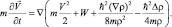 (4.6)
(4.6)
Для свободных частиц, когда 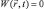 и
и 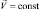 уравнение (4.6) имеет тривиальное решение ρ = const, которое соответствует волнам де Бройля и которое ранее использовалось для описания квантовой бесстолкновительной плазмы [6]. Однако система уравнений (4.5) и (4.6) помимо тривиального решения имеет и другие решения, что увеличивает предсказательные возможности квазигидродинамического представления для движения квантовых частиц.
уравнение (4.6) имеет тривиальное решение ρ = const, которое соответствует волнам де Бройля и которое ранее использовалось для описания квантовой бесстолкновительной плазмы [6]. Однако система уравнений (4.5) и (4.6) помимо тривиального решения имеет и другие решения, что увеличивает предсказательные возможности квазигидродинамического представления для движения квантовых частиц.
Умножим уравнение (4.6) на 2m и устремим m → 0, получим
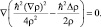 (4.7)
(4.7)
Первое интегрирование этого уравнения дает:
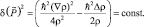 (4.8)
(4.8)
Здесь принято обозначение константы интегрирования для движения безмассовых частиц в виде квадрата квантового импульса [7]. В качестве решения системы уравнений (4.6) и (4.8) можно воспользоваться готовым решением из [7] в виде:
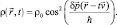 (4.9)
(4.9)
Это решение описывает волну плотности вероятности, которая распространяется в пространстве с волновым вектором 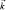 :
:
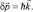 (4.10)
(4.10)
А закон дисперсии для частоты колебаний в этой волне запишется в виде:
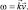 (4.11)
(4.11)
Поскольку не существует макроскопический импульс 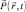 , который связан с массой частицы, то векторы
, который связан с массой частицы, то векторы 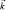 и
и  совпадают по направлению. Для энергии квантов этого поля имеем линейный закон дисперсии:
совпадают по направлению. Для энергии квантов этого поля имеем линейный закон дисперсии:
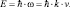 (4.12)
(4.12)
Здесь скорость безмассовых квантовых частиц не определена. Это могут формально быть, например, длинноволновые акустические фононы, или фотоны, распространяющиеся со скоростью света, когда v = c. Здесь не требуется лоренцевская инвариантность исходных уравнений, поскольку масса покоя фотонов равна нулю.
Если частица движется со скоростью света v = c, то имеем:
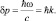 (4.13)
(4.13)
Это есть стандартное выражение для импульса фотона. Пользуясь формулами (4.10) и (4.11) выражение для плотности вероятности (9) можно переписать в виде:
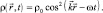 (4.14)
(4.14)
Плотность электромагнитной энергии в вакууме для плоских электромагнитных волн равна [8]
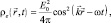 (4.15)
(4.15)
где E0 – амплитуда электрического поля. Можно видеть, что плотность вероятности, описывающая движение частиц с нулевой массой, согласуется с плотностью электромагнитной энергии с точностью до нормировки. Тогда плотность потока вероятности
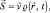
согласуется с точностью до коэффициента с плотностью потока электромагнитной энергии (вектор Умова – Пойтинга).
Полученные результаты ещё раз убеждают, что квантовые квазигидродинамические уравнения или представление плотности вероятности, на наш взгляд, более полно описывают волновую природу движения квантовых частиц.
Эта статья была написана к 120-летию со дня рождения Луи де Бройля (15.08.1892 г.), к которому автор на протяжении своей жизни питает все возрастающий пиетет, и опубликована в [7]. С течением времени содержание статьи по необходимости изменилось. Здесь изложен её новый вариант.
Литература
1. Де Бройль Луи. Избранные научные труды. Т. 1. Становление квантовой механики. М.: Логос. 2010. 552 с.
2. Ghosh S.K., Deb B.M. Densities, Density-Functionals and Electron Fluids // Physics Reports (Review Section of Physics Letters). – 1982. V. 92, № 1. – P. 1-44.
3. Алексеев Б.В., Абакумов А.И. Об одном подходе к решению уравнения Шредингера // Доклады Академии наук – 1982. Т. 262. – С. 1100-1102.
4. Вопросы причинности в квантовой механике. Сб. переводов / Под ред. Я.П. Терлецкого и А.А. Гусева. – М.: ИЛ 1955. С. 34.
5. Чаплыгин Ю.А., Неволин В.К., Петухов В.А. Эффект охлаждения анода при автоэлектронной эмиссии с катода. Доклады академии наук. 2011. Т. 436. № 2. С. 1-3.
6. Кузелев М.В., Рухадзе А.А. О квантовом описании линейных кинетических свойств бесстолкновительной плазмы. УФН. 1999. Т. 169. № 6. С. 687-689.
7. Неволин В.К. Квантовая физика и нанотехнологии // М.: Техносфера. – 2013. – 127 с. Nevolin V.K. Quantum Physics and Nanotechnology. http:/arxiv.org/abs/1106.0973v1.
8. Неволин В.К. Квантовый транспорт в устройствах электроники // М.: Техносфера. – 2012. – 89 с.
9. Власов А.А. Макроскопическая электродинамика. М.: ГизТТЛ. 1955. С. 48.
