
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6. Вихревые (торсионные) поля плотности вероятности квантовых частиц
Наша задача – показать, что при вращательном движении квантовой частицы возможно существование и распространение вихревых (торсионных) волн плотности вероятности. Это можно доказать, решая нерелятивистское уравнение Шредингера в представлении плотности вероятности.
Обычно используется гидродинамическое представление уравнения Шредингера в виде [1–4]:
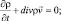 (6.1)
(6.1)
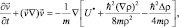 (6.2)
(6.2)
где  – макроскопическая скорость частицы;
– макроскопическая скорость частицы; 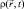 – плотность вероятности; m – масса частицы; ħ – постоянная Планка; U* – потенциальная энергия, в которую по необходимости включают электромагнитные составляющие. Возможен учет и спиновых взаимодействий [5]. Эти уравнения неоднократно получались, начиная с Е. Маделунга и Д. Бома [1], путем представления волновых функций в квазиклассическом виде.
– плотность вероятности; m – масса частицы; ħ – постоянная Планка; U* – потенциальная энергия, в которую по необходимости включают электромагнитные составляющие. Возможен учет и спиновых взаимодействий [5]. Эти уравнения неоднократно получались, начиная с Е. Маделунга и Д. Бома [1], путем представления волновых функций в квазиклассическом виде.
Уравнение для плотности вероятности из уравнения Шредингера можно получить и другим путем, если положить [6]:
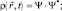
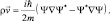
Тогда имеем, как и прежде, закон сохранения плотности вероятности (6.1) и уравнение движения в виде:
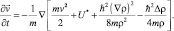 (6.3)
(6.3)
Это уравнение отличается от уравнения (6.2). Если положить, что всегда имеет место безвихревое движение поля плотности вероятности, т.е.
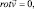
то из уравнения (6.3) получается уравнение (6.2).
Таким образом, в гидродинамическом представлении с помощью уравнений (6.1) и вида (6.2) отсутствует возможность описания вихревых движений поля плотности вероятности квантовых частиц. Систему уравнений (6.1), (6.3) будем называть в отличие от гидродинамического представления представлением плотности вероятности (ранее мы называли его квазигидродинамическим представлением [6]).
Пусть квантовая частица совершает вращательное движение с угловой скоростью ω и радиусом R. Используем цилиндрическую систему координат, тогда орбитальная составляющая скорости vφ = ωR и пусть частица двигается вдоль оси z с макроскопической скоростью vz.
Тогда уравнение (6.1) запишется в виде:
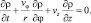 (6.4)
(6.4)
Решение этого уравнения представим таким образом:
ρ = ρ(α); 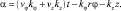 (6.5)
(6.5)
Первый интеграл уравнения (6.3), учитывая постоянство скоростей vφ и vz, запишется в виде:
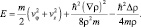 (6.6)
(6.6)
Обозначим:
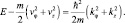 (6.7)
(6.7)
Это можно сделать в силу того, что полная энергия квантовой частицы состоит из макроскопической и квантовой составляющей энергий [6]. Аддитивность составляющих полной энергии можно видеть и в правой части уравнений (6.3) и (6.6).
Уравнение (6.6) с учетом (6.7) и (6.5) будем иметь вид:
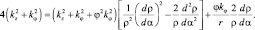 (6.8)
(6.8)
Нам необходимо найти волновое решение этого уравнения. Будем решать его методом последовательных приближений. Положим, что φ << 1 во всех коэффициентах, входящих в уравнение. Тогда получится уравнение:
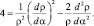 (6.9)
(6.9)
Решение этого уравнения найдено в [6] и имеет вид:
ρ = ρ0cos2α. (6.10)
Это решение справедливо при любом значении α, в том числе и φ. Подставляя решение (6.10) в (6.8), получаем алгебраическое трансцендентное уравнение:
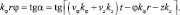 (6.11)
(6.11)
Формулы (6.10) и (6.11) описывают решения дифференциальных уравнений (6.4) и (8).
Перепишем решение (6.10) в другом виде:
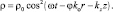 (6.12)
(6.12)
Здесь ω – частота осцилляций волны плотности вероятности. Имеем линейный закон дисперсии:
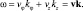 (6.13)
(6.13)
Вектор макроскопической скорости и волновой вектор не совпадают по направлению. Частота осцилляций волны является суммой осцилляций орбитального и поступательного движений. Решение (6.12) должно удовлетворять условию периодичности в любой момент времени и в любой точке z. Тогда
kφrn = n, n = 1, 2, 3, ... (6.14)
Орбитальный радиус поля плотности вероятности квантуется с равноудаленными расстояниями между окружностями:
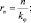
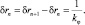 (6.15)
(6.15)
С учетом (6.15) уравнение (11) запишется в виде:
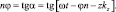 (6.16)
(6.16)
Уравнение (6.16) обеспечивает синхронизацию угловой переменной с текущим временем в каждой точке на оси z. Найдем из уравнения (6.16) угловую скорость вращения поля плотности вероятности φ.
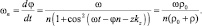 (6.17)
(6.17)
Орбитальная скорость вращения поля плотности вероятности равна:
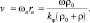 (6.18)
(6.18)
Можно видеть, что орбитальная скорость вращения поля вероятности в любой точке осциллирует в пределах от 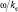 до
до 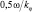 .
.
Квантовое уравнение в виде (6.8) не зависит от массы частицы. Стало быть, это уравнение может описывать и движение безмассовых квантовых частиц, имеющих линейный закон дисперсии, в частности, длинноволновых фононов, фотонов и др. частиц. Благо, что в нерелятивистких уравнениях не имеют значения величины скорости для безмассовых частиц. В частности, в [6] было показано, что плотность вероятности и плотность потока вероятности с точностью до обозначений описывают плотность электромагнитной энергии для плоских электромагнитных волн в вакууме и вектор Умова – Пойтинга. В этом можно убедиться, используя формулы (6.12) и (6.13). Нужно положить vφ и φ равными нулю и vz = c, где c – скорость света. Для квантовомеханического описания движения безмассовых частиц (или частиц с исчезающее малой массой покоя) используются квантовый импульс и макроскопическая скорость. Однако континуум таких невзаимодействующих частиц, например, фотонов, описывает различные электромагнитные волны в зависимости от величины волнового вектора или длины волны.
Использование скорости света для безмассовых частиц в нерелятивисткой квантовой механике не приводит к противоречиям. Скорость света присутствует и в классических уравнениях Максвелла, определяя скорость распространения электромагнитных волн в вакууме. Можно предположить, что уравнение (6.8) может описывать квантовые свойства пучков света, в частности, аксиконов [7, 8], поскольку излучение в виде концентрических окружностей (6.15) во фронтальной плоскости напоминает обыкновенные аксиконы.
Для вихревого движения плотности поля вероятности частиц с массой покоя отличной от нуля необходимо выполнение условий:
vφ, vz << c,
где с – скорость света. Составляющие волнового вектора можно определять следующим образом:
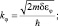
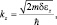 (6.19)
(6.19)
где δεφ, δεz – квантовые составляющие энергии орбитального и поступательного движения. Эти энергии отличаются от полных энергий согласно [6] и могут быть измерены отдельным способом [9]. Для оценок воспользуемся тем обстоятельством, что в традиционной квантовой механике полная энергия свободных квантовых частиц отождествляется с её квантовой величиной, что завышает значения волновых векторов. Положим:
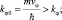
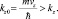 (6.20)
(6.20)
Например, если иметь дело с «холодными» нейтрино, масса покоя которых оценивается как 10–33 г [10], то величина
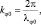
где λφ0 – длина волны, при скоростях частиц vφ ~ 109 см/с λφ > 6∙10–3 см. Эта оценка показывает, что континуум невзаимодействующих «холодных» нейтрино может создавать, в том числе, макроскопические вихревые (торсионные) поля плотности вероятности.
Система квантовых уравнений движения с физическими переменными (6.1), (6.3), на наш взгляд, более адекватно отражает исходное уравнение Шредингера, чем система уравнений (6.1), (6.2), поскольку позволяет описывать вихревые поля плотности вероятности квантовых частиц. В нерелятивистском приближении для частиц с линейным законом дисперсии таких как: низкочастотные фононы, фотоны, «холодные» нейтрино возможны вихревые (торсионные) поля плотности вероятности. Существование вихревых полей оптических фотонов в виде аксиконов это реальность [7, 8].
Литература
1. Ghosh S.K., Deb B.M. Densities, Density-Functional and Electron Fluids // Physics Reports (Review Section of Physics Letters). – 1982.
V. 92, № 1. – P. 1-44.
2. Алексеев Б.В., Абакумов А.И. Об одном подходе к решению уравнения Шредингера // Доклады Академии наук – 1982. Т. 262. – С. 1100-1102.
3. Кузелев М.В., Рухадзе А.А. О квантовом описании линейных кинетических свойств бесстолкновительной плазмы. УФН, 1999, т. 169, № 6. С. 687-689.
4. Кузелев М.В., Рухадзе А.А. Нерелятивисткая квантовая теория вынужденных черенковского излучения и комптоновского рассеяния в плазме. ФНТ, 2011, Т. 37, № 9/10 С. 1-7.
5. Микаэлян М.А. Гидродинамическая формулировка уравнений Паули. Прикладная физика. 2003. № 3. С. 5-9.
6. Неволин В.К. Квантовый транспорт в устройствах электроники. – М., Техносфера. – 2012. – 87 с.
7. Волостников В.Г. Спиральные пучки света. http:/www.fian.smr.ru/beam1.htm.
8. Скиданов Р.В., Ганчевская С.В. Формирование пучков Бесселя вихревыми аксиконами. Компьютерная оптика. 2014. Т. 38. № 3. С. 463-468.
9. Неволин В.К. Патент РФ. Способ измерения энергии квантовой нелокальности частиц, совершающих инфинитное движение. № 2444711 с приоритетом от 30.01.2009 г. Бюл. № 7, 2012.
10. Лобашов В.М. Измерение массы нейтрино в бета-распаде трития. Вестник РАН. 2003. № 73(1). С. 14-27.
