Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

АТОМ ВОДОРОДА. ЧТО НОВОГО?

Неволин В. К.,

7. Атом водорода – что нового?

Можно ли узнать что-нибудь новое об атоме водорода? Кажется, в квантовой механике он изучен самым детальным образом, тем более что многие задачи о пространственной структуре и состояниях этого атома решаются аналитически. Однако можно показать, что плотность вероятности нахождение электрона, двигающегося вокруг ядра, в отличие от традиционных представлений структурирована, а это должно приводить к уточнению известных эффектов и, возможно, к предсказанию новых. Для доказательства такого утверждения целесообразно решить задачу об атоме водорода в представлении плотности вероятности, непосредственно описывающую ее распределение во всех возможных квантовых состояниях рассматриваемого атома.

Уравнения для непрерывного движения квантовой частицы массы m0 в произвольном внешнем поле 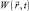в представлении плотности вероятности имеют вид [1–3]:

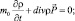(7.1)

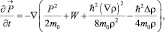(7.2)

где 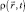 – пространственно-временное распределение плотности вероятности частицы;  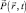– ее макроскопический импульс;  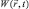– произвольная потенциальная энергия.

Для атома водорода в традиционной квантовой механике вычислен спектр энергий и найдены волновые функции. Для стационарного пространственно ограниченного движения электрона в поле ядра с зарядом Z система уравнений (7.1) и (7.2) запишется в виде:

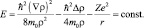(7.3)

Волновые функции для атома водорода найдены, например, в [4]. Их можно записать в виде:

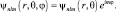(7.4)

Здесь n, l, m – квантовые числа. Поскольку ψnlm(r, θ) – функция вещественная, то выражение для плотности вероятности имеет вид:

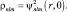(7.5)

Квантовая величина ρnlm показывает наличие осевой симметрии атома. Подставляя (7.5) в уравнение движения (7.3) и проведя все необходимые дифференцирования и сокращения подобных членов, получим стандартное уравнение Шредингера для электрона в кулоновском поле:

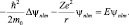(7.6)

Решение его позволяет получить энергетический спектр электрона в атоме и угловое распределение плотности вероятности. В общем виде уравнение имеет вид:

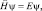
где оператор Гамильтона равен:

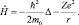(7.7)

Для отыскания собственных значений энергии к аналогичному виду можно привести уравнение (7.3):

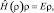(7.8)

где нелинейный оператор Гамильтона равен:

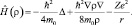(7.9)

Сравнивая (7.7) и (7.9) можно увидеть, что для аналитических решений задач о пространственно ограниченном движении квантовых частиц предпочтительнее линейный оператор (7.7).

Однако решение уравнения (7.8) с оператором (7.9) позволяет получить новые представления о движении электрона в атоме водорода. Рассматривая (7.4) и (7.5) можно видеть, что фаза волновой функции с магнитным квантовым числом исчезает при описании пространственно ограниченного движения с помощью плотности вероятности (7.5) и, как кажется, из решения должно исчезнуть само магнитное число. Это не так. Решая систему уравнений (7.8) и (7.9) методом разделения переменных, как это делается для уравнения (7.6) и, предположив ρ(r, θ, φ) = ρr(r)ρθ(θ)ρφ(φ), удается получить связанные между собой две константы разделения и следующие уравнения:

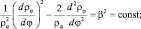(7.10)

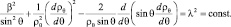(7.11)

Заменим переменные в уравнении (7.11):

ρθ = γ2(θ) и ξ = cos θ,

и сведем это уравнение к известному уравнению, решенному для атома водорода с угловой переменной θ. Решение такого уравнения можно представить в виде полинома Лежандра [4]. Для нас важно, что константы разделения в этом уравнении квантуются:

λ2 = 4l(l + 1), (7.12)

где l = 0, 1, 2, 3, ...

и β2 = 4m2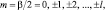

где l называю обычно орбитальным квантовым числом; m – магнитным квантовым числом.

Уравнение (7.10) решаем подстановкой

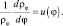
Тогда 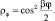Чтобы ρφ была однозначной функцией для константы β, должны выполняться соотношения β = 0, ±1, ±2, ±3, ... Однако не все значения β удовлетворяют соотношениям (7.12), а только ноль и четные значения. Окончательно имеем

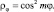
Из полученных решений следует, что в атоме водорода могут существовать: симметрия с m = 0 и оси симметрии первого, второго, третьего и последующего порядков. Это есть структурированное распределение плотности вероятности по углу j с сохранением известных значений магнитных чисел, отличающееся от традиционных решений (7.4) и (7.5). Оно показывает, что для возбужденных атомов наряду с существованием орбитальных токов должны иметь место структурирование электронной плотности вероятности при движении по углу j (рис. 7.1): для m = ±1 в виде «двухлистника», для m = ±2 «четырехлистника» и т.д.

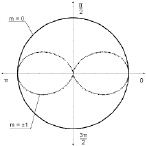
Рис. 7.1. Структурирование электронной плотности вероятности по углу φ

В традиционной модели атома водорода отсутствует пространственно структурированное распределение электронной плотности
вероятности при движении по углу φ и можно думать, что приведенные выше рассуждения это математический фокус и такого быть не может. Однако за этим стоит вполне определенная физика явлений. Дело в том, что когда квантовая частица помимо собственно квантового движения совершает ещё какое-то механическое движение, например, поступательное, то фактически частица участвует в двух движениях и в этом случае её плотность вероятности структурируется в пространстве (см. подробнее в [3]). Электрон в атоме водорода в возбужденном состоянии помимо квантового движения совершает ещё вращательное механическое движение с вполне определенным моментом количества движения и, следовательно, его электронная плотность вероятности должна быть структурирована в пространстве.

Проверка полученного результата на экспериментальном факте показывает следующее. Известно, что средний дипольный момент атома водорода равен нулю [4]. Компонента электрического момента электрона в проекции на ось z равна 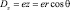. Тогда

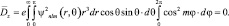
Второй интеграл по dq – равен нулю, поскольку подынтегральное выражение является нечетной функцией cos q в симметричных пределах. Это и требовалось доказать.

Таким образом, в атоме водорода должно существовать структурированное распределение плотности вероятности электрона при движении по углу φ для возбужденных состояний, что возможно будет сказываться при его взаимодействии с внешними полями и другими квантовыми объектами.

Литература

1. Ghosh S.K., Deb B.M. Densities, Density-Functionals and Electron Fluids // Physics Reports (Review Section of Physics Letters). – 1982. V. 92, № 1. – P. 1-44.

2. Алексеев Б.В., Абакумов А.И. Об одном подходе к решению уравнения Шредингера // Доклады Академии наук – 1982. Т. 262. – С. 1100-1102.

3. Неволин В.К. Квантовый транспорт в устройствах электроники // М.: Техносфера. – 2012. – 87 с.

4. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М.: Наука 1974. С. 130.