Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Обухов А. Г., Сорокина Е. М.,
§7. Программно-вычислительный комплекс и несколько способов его тестирования
Для численного решения полной системы уравнений Навье – Стокса был разработан программно-вычислительный комплекс, в основе которого лежат четыре программы, получившие свидетельства о государственной регистрации.
Программно-вычислительный комплекс состоит из пяти основных блоков (рис. 7.1):
– блока входных данных;
– расчетного блока;
– блока расчета энергетических характеристик течений;
– блока построений линий тока течений;
– блока хранения расчетной информации.
Исходные данные – шаги по пространству и времени, масштабные значения используемых величин, начальные и краевые условия, коэффициенты вязкости и теплопроводности, используемые в расчетах константы – размещаются пользователем в блоке входных данных перед началом работы программно-вычислительного комплекса. При этом предусмотрена возможность выбора необходимых значений входных параметров из нескольких возможных.
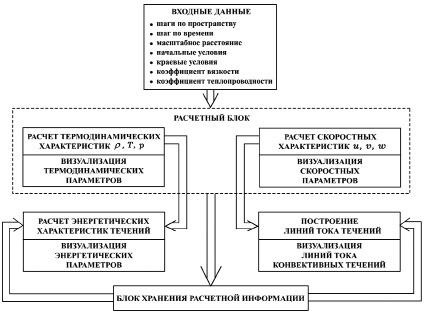
Рис. 7.1. Программно-вычислительный комплекс
Исходные входные данные поступают основной расчетный блок, в котором с помощью явной разностной схемы с учетом начальных и граничных условий численно строятся решения полной системы уравнений Навье – Стокса и определяются термодинамические и скоростные характеристики возникающих конвективных потоков во всех узлах расчетной области в различные последующие моменты времени.
Результаты работы расчетного блока могут передаваться в качестве исходных данных для двух других блоков – блока расчетов энергетических характеристик и блока построения линий тока.
Тестирование программно-вычислительного комплекса осуществлялось несколькими способами.
Во-первых, в качестве начального течения задавались параметры стационарного точного решения при учете силы тяжести, описанного в §4 и зависящего только от переменной z. В качестве контроля тестирования в процессе нестационарного трехмерного расчета отслеживались изменения газодинамических параметров по ходу счета. Они, естественно, менялись, но, как оказалось, только в пределах вычислительной погрешности метода: в четвертом-пятом знаках после запятой. Поэтому можно сделать вывод, что нестационарным расчетом точное стационарное решение передается верно.
Во-вторых, в присутствии силы тяжести были проведены расчеты нестационарного конвективного течения, возникающего при задании на плоскости z = 0 постоянного теплового режима, локально превышающего распределение температуры при z = 0 у точного стационарного течения. Через 10000 шагов по времени расчеты привели практически к стационарному конвективному течению, параметры которого хоть и менялись с последующим увеличением времени, но незначительно и картина линий тока оставалась практически неизменной. После того, как локальный прогрев был убран, то есть на плоскости z = 0 снова задавалась постоянная температура, значение которой бралось из точного стационарного решения, конвективный поток за 500 шагов по времени исчезал, и течение вновь становилось стационарным, зависящим только от координаты z и совпадающим с точным стационарным решением.
В-третьих, нестационарным трехмерным расчетом с использованием созданного комплекса программ были повторены расчеты одномерных нестационарных течений [119]. Начальные данные вносили гладкое возмущение в однородный покоящийся без воздействия силы тяжести газ. Это возмущение распространялось, и с течением времени передний фронт возмущения становился все круче. Это передает возникновение размазанного ударного перехода, описанного Р. Беккером [120]. Сравнение результатов расчетов из работы [119] и полученных по описываемой программе также показало их совпадение в пределах вычислительной погрешности.
Также проведен расчет одномерного нестационарного течения сжимаемого вязкого теплопроводного газа. В начальный момент времени плотность газа постоянна и равна единице, скорость газа равна нулю, то есть u = v = w = 0, а температура задана следующим соотношением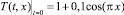 
, и на границах отрезка 0 ≤ x ≤ 1 заданы условия прилипания и теплоизоляции
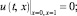
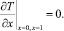(7.1)
Результаты расчетов газодинамических параметров в некоторые фиксированные моменты времени для z0 = 0,05 представлены на последующих рисунках. На рис. 7.2 и 7.3 приведены графики функций ρ(x, y) и T(x, y) на 1000 временном шаге. При увеличении времени счета значения плотности и температуры постепенно приближаются к единице, сохраняя при этом косинусоидальную зависимость от x.
На рис. 7.4 и 7.5 приведены результаты расчета первой компоненты u скорости для двух моментов времени. Видно, что за представленный промежуток времени параболическая зависимость этой компоненты скорости постепенно переходит в волнообразную зависимость от координаты x.
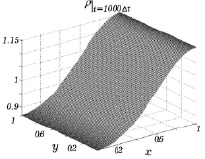
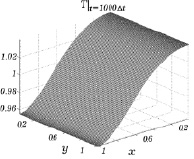
Рис. 7.2 Рис. 7.3
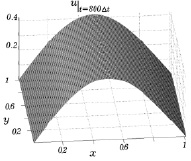
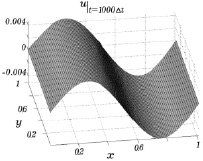
Рис. 7.4 Рис. 7.5
На рис. 7.6 и 7.7 изображены результаты расчетов второй компоненты v скорости для двух моментов времени. Как следует из приведенных рисунков, эта компонента скорости равна нулю во всех точках за исключением небольших пиков по углам. Величина этих пиков имеет порядок 10–8 и никак не сказывается на вычислении плотности, температуры и первой компоненты скорости. Этот расчетный эффект связан с неизбежным незначительным скачком второй компоненты скорости в вертикальных гранях расчетной области.
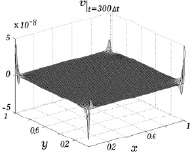
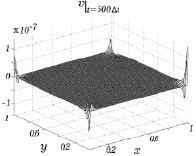
Рис. 7.6 Рис. 7.7
На рис. 7.8 и 7.9 приводятся результаты расчетов третей компоненты w скорости для трех моментов времени. При расчете этой компоненты скорости в начальные моменты времени вблизи плоскостей x = 0 и x = 1 возникают «иглы», величина которых 10–17...10–16. Приблизительно к 400 расчетному шагу по времени эти «иглы» исчезают и графические зависимости вертикальной составляющей скорости становятся гладкими поверхностями, а отличия значений скорости от нуля имеют величину порядка 10–12.
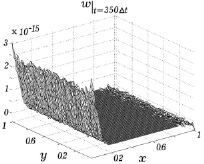
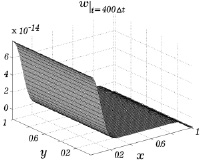
Рис. 7.8 Рис. 7.9
Таким образом, в приведенном трехмерном расчете фактическая зависимость ρ, u, T только от одной пространственной переменной и фактическое равенство нулю функций v и w полностью соответствуют моделированию одномерного нестационарного течения [119, 121].
В данной главе рассмотрена математическая модель для описания начальной стадии сложных конвективных течений сжимаемого теплопроводного газа, основанная на численном решении полной системы уравнений Навье – Стокса. Эта модель наиболее адекватно описывает физические процессы в конвективных течениях, поскольку учитывает диссипативные свойства движущейся сжимаемой сплошной среды – вязкости и теплопроводности.
Предложены начальные и граничные условия для численного построения решений полной системы уравнений Навье – Стокса и их конечно-разностная аппроксимация.
Описан программно-вычислительный комплекс на основе четырех программ, позволяющий проводить численное решение задач, связанных с описанием указанных конвективных течений и определения их основных параметров. А также приведены результаты тестирования программно-вычислительного комплекса.