Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТРЕХМЕРНЫХ НЕСТАЦИОНАРНЫХ КОНВЕКТИВНЫХ ТЕЧЕНИЙ СЖИМАЕМОГО ВЯЗКОГО ТЕПЛОПРОВОДНОГО ГАЗА

Обухов А. Г., Сорокина Е. М.,

§8. Численное моделирование конвективных течений при локальной кольцевой схеме нагрева

В данном параграфе рассматриваются результаты математического и численного моделирования трехмерных конвективных течений сжимаемого вязкого теплопроводного газа в условиях действия силы тяжести. Коэффициенты вязкости и теплопроводности полагаются постоянными. За начальные условия принимаются функции, являющиеся точным аналитическим решением полной системы уравнений Навье – Стокса. В качестве краевых предлагаются условия, описанные в пятом параграфе.

Конвективный поток газа инициируется кольцеобразным нагревом подстилающей поверхности. Решения полной системы уравнений Навье – Стокса строятся численно по явной разностной схеме в кубе с единичной длиной ребра. Приведены результаты расчетов плотности, температуры, давления, трех составляющих векторов скоростей частиц газа, а также построены линии тока в начальной стадии формирования свободного конвективного потока.

Начальные условия при описании конвективных течений сжимаемого вязкого теплопроводного газа в случае постоянных значений коэффициентов вязкости и теплопроводности берутся в виде функций, задающих известное точное аналитическое решение [94] системы (4.1):

u = 0; v = 0; w = 0; (8.1)

T0(z) = 1 – kz; 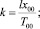I = 0,0065 К/м; x00 = 10 м; T00 = 288 °К; (8.2)

ρ0(z) = (1 – kz)v–1; 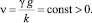(8.3)

Расчетная область представляет собой куб с длинами сторон x0 = 1, y0 = 1 и z0 = 1 вдоль осей Ox, Oy и Oz соответственно.

Для плотности на всех шести гранях куба x = 0, x = x0, y = 0, y = y0, z = 0, z = z0 задается «условие непрерывности» [95].

Для температуры на пяти гранях куба x = 0, x = x0, y = 0, y = y0, z = 0 z = z0 задаются условия теплоизоляции («условие симметрии»)[95].

На нижней плоскости z = 0 значения температуры в кольце между концентрическими окружностями с безразмерными значениями радиусов 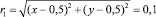и 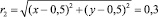 заданы в виде функции

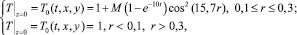(8.4)

моделирующей кольцеобразный локальный нагрев нижней грани расчетного куба. Задаваемый коэффициент M в формуле (8.4) определяет максимальное значение температуры нагрева в разных вариантах расчета и равен разности между максимальным безразмерным значением температуры локального нагрева и масштабным безразмерным значением температуры M = Tmax – 1.

Краевые условия для компонент вектора скорости газа на всех шести гранях берутся из «условий непротекания» для нормальной к граничной поверхности составляющей вектора скорости и «условиям симметрии» для двух других компонент вектора скорости течения [95]. Данные краевые условия фактически означают рассмотрение конвективного течения сжимаемого вязкого теплопроводного газа в непроницаемой и теплоизолированной кубической емкости.

Расчетная область заполняется трехмерной сеткой узлов пересечения трех семейств плоскостей с разностными шагами по трем пространственным переменным Δx = Δy = 0,01, Δz = 0,1, и шагом по времени Δt = 0,001.

Расчеты проводились при масштабных размерных значениях плотности, скорости, расстояния и времени равными соответственно ρ00 = 1,2928 кг/м3, u00 = 333 м/с, x00 = 10 м, Безразмерное и соответствующее размерное значение коэффициента M следующие: M = 0,125, M* = 36 °C.

На рис. 8.1–8.4 представлены результаты расчета плотности газа в виде графиков функции двух переменных ρ(x, y) на фиксированной высоте z = 0,5 (размерное значение 5 м) для четырех расчетных шагов по времени. По осям координат x и y отложены безразмерные значения расстояния.

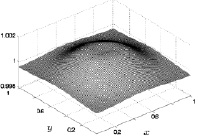
Рис. 8.1. Плотность на 50 шаге Рис. 8.2. Плотность на 300 шаге

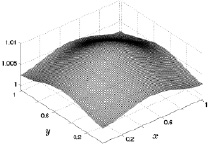
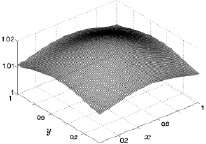
Рис. 8.3. Плотность на 3000 шаге Рис. 8.4. Плотность на 10000 шаге

Из приведенных рисунков видно, что поведение плотности газа за рассчитанное время можно характеризовать следующим образом.

Периферийные значения плотности, близкие к боковым граням расчетной области, для каждого отдельного фиксированного момента времени меняются незначительно. В центральной части боковых граней значения плотности больше, а в углах – меньше. Это, по-видимому, связано с более интенсивным притоком газа к центрам боковых граней, чем к областям, близким к вертикальным ребрам.

Общее фоновое безразмерное значение плотности с течением времени увеличивается от 1 до 1,02, что соответствует изменению размерных значений в пределах от 1,2928 до 1,3187 кг/м3.

Распределение плотности в начале нагрева имеет форму кольца, центр которого совпадает с геометрическим центром квадратного сечения расчетной области, а радиус его совпадает с радиусом кольца нагрева. С течением времени происходит расширение кольца с повышенными значениями плотности и его размывание в пространстве и к 10000 расчетному шагу по времени область повышенных значений плотности практически достигают боковых граней расчетного куба.

С течением времени меняется и геометрическая симметрия плотности. В начале кольцеобразного прогрева нижней поверхности плотность газа имеет четко выраженную центральную симметрию, а с течением времени область центральной симметрии, расширяясь к боковым граням, меняется на прямоугольную.

На рис. 8.5–8.8 приведены результаты расчета температуры газа в виде графиков функции двух переменных T(x, y) на фиксированной высоте z = 0,5 (размерное значение 5 м) для четырех таких же расчетных шагов по времени.

Поведение рассчитанных значений температуры как функций координат и времени отлично от аналогичного поведения плотности. Периферийные значения температуры в начале прогрева также близки к единичному, а с течением времени наблюдаются немонотонные их изменения. Фоновые безразмерные значения температуры в областях, близких к боковым граням расчетного куба, с течением времени изменяются существенно меньше,
чем значения плотности. В рассчитанном диапазоне временных шагов эти значения температуры меняются в пределах от 1 до 1,0025 (в размерных значениях от 288 до 288,72 °К).

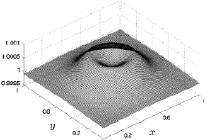
Рис. 8.5. Температура на 50 шаге Рис. 8.6. Температура на 300 шаге

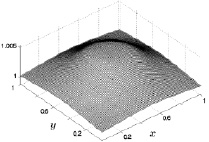
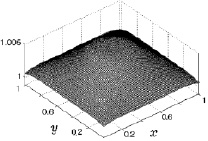
Рис. 8.7. Температура на 3000 шаге Рис. 8.8. Температура на 10000 шаге

Что касается геометрической симметрии, то с течением времени она для температуры практически не меняется со временем. В начале кольцеобразного прогрева нижней поверхности температура газа имеет четко выраженную кольцеобразную центральную симметрию, которая с течением времени расширяясь к боковым граням, сохраняет кольцеобразный характер. Отличием поведения температуры от поведения плотности является существенно большее увеличение ее в центральной области до значений 1,01 (размерное значение 290,88 °К). Как видно из приведенного рис. 8.8 это увеличение температуры имеет вид колокола, что связано с более интенсивным прогревом центральной области. Кольцеобразный нагрев подстилающей поверхности, очевидно, сказывается на поведении температуры нагрева на этой фиксированной высоте в центральной части исследуемой области и визуализируется в виде воронки в центре колоколообразной поверхности.

На рис. 8.9–8.12 приведены результаты расчета давления газа в виде графиков функции двух переменных p(x, y) на фиксированной высоте z = 0,5 (размерное значение 5 м) для четырех расчетных шагов по времени. Поскольку давление есть произведение плотности на температуру, то его поведение как функции координат и времени во многом совпадает с аналогичным поведением плотности и температуры.

Общим в поведении давления в рассмотренном промежутке времени является рост фонового периферийного значения от 1 до 1,023 (размерные значения от 100 до 102,3 кПа) и постепенный переход от кольцевой структуры к колоколообразной при сохранении осевой центральной симметрии. Превышение максимальных значений давления над фоновыми для 10000 расчетного шага по времени составляет 0,007 (размерное значение 700 Па).

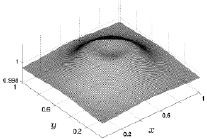
Рис. 8.9. Давление на 50 шаге Рис. 8.10. Давление на 300 шаге

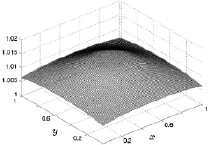
Рис. 8.11. Давление на 3000 шаге Рис. 8.12. Давление на 10000 шаге

Кроме того, при тех же начальных и краевых условиях было осуществлено математическое моделирование и проведен численный расчет скоростных характеристик начальной стадии формирования трехмерного нестационарного конвективного течения газа, вызванного локальным кольцеобразным прогревом нижней поверхности расчетной области.

На рис. 8.13–8.16 представлены графики x-й компоненты скорости газа для фиксированной высоты z = 0,5 (размерное значение 5 м) для четырех фиксированных расчетных шагов по времени. На осях координат x, y отложены безразмерные значения расстояния.

Из приведенных рисунков видно, что поведение первой компоненты скорости газа за рассчитанное время можно характеризовать следующим образом. В самом начале прогрева, соответствующем 50 расчетному шагу
по времени (рис. 8.13), периферийные значения скорости практически равны нулю. В центре расчетной области скорости малы по значению, противоположны по знаку, и имеют четко выраженную кольцевую структуру, соответствующую кольцевой схеме нагрева нижней плоскости. Положительные и отрицательные значения первой компоненты скорости, находящиеся за пределами кольцевого нагрева, описывают расходящееся от центра вдоль радиуса движение газа. Разные же по знаку скорости, но находящиеся внутри кольца нагрева, соответствуют сходящемуся вдоль радиуса к центру потоку газа. Максимальные безразмерные значения модулей скоростей для данного расчетного момента времени составляют 2∙10–10 (размерное значение 6,66∙10–8 м/с).

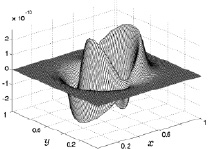
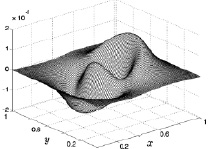
Рис. 8.13. Скорость u на 50 шаге Рис. 8.14. Скорость u на 300 шаге

Для 300 расчетного шага по времени (рис. 8.14) область, соответствующая движению газа от центра расширяется, а область движения газа к центру сужается. При этом максимальные значения модулей скорости увеличиваются до 2∙10–5 (размерное значение 0,0067 м/с). Такие изменения первой компоненты скорости течения газа согласуются с нарастанием температуры кольцеобразного нагрева. Значения скорости на плоскостях x = 0 и x = 1 равны нулю согласно «условию непротекания», установленному для этих граней расчетной области. Значения же скоростей на гранях y = 0 и y = 1 начинают заметно меняться.

Для 3000 расчетного шага по времени (рис. 8.15) область, соответствующая движению газа от центра сместилась еще ближе к боковым граням, а область движения газа к центру практически исчезла. При этом максимальные значения модулей скорости увеличиваются до 0,01 (размерное значение 3,33 м/с). Значения скорости на плоскостях x = 0 и x = 1 по-прежнему равны нулю, а значения скоростей на гранях y = 0 и y = 1 изменяются по синусоидальному закону.

На 10000 расчетном шаге по времени (рис. 8.16) область, соответствующая движению газа от центра практически дошла до боковых граней. Максимальные значения модулей скорости увеличились до 0,04 (размерное значение 13,32 м/с). Значения скорости на плоскостях x = 0 и x = 1 равны нулю, а значения скоростей на гранях y = 0 и y = 1 волнообразно изменяются.

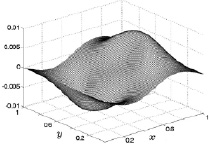
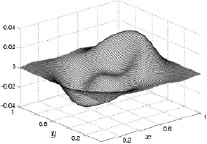
Рис. 8.15. Скорость u на 3000 шаге Рис. 8.16. Скорость u на 10000 шаге

Расчеты показали, что изменение x-й компоненты скорости газа имеет ярко выраженный нестационарный характер. Кроме того, в начальные моменты времени общая структура скоростей имеет центральную симметрию, а с течением времени она изменяется и приобретает прямоугольный характер.

На рис. 8.17–8.20 представлены графики y-й компоненты скорости газа для фиксированной высоты z = 0,5 (размерное значение 5 м) для четырех фиксированных расчетных шагов по времени. На осях координат x, y отложены безразмерные значения расстояния.

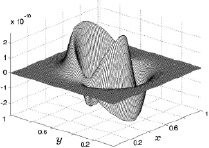
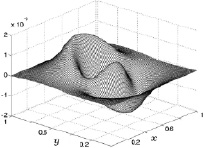
Рис. 8.17. Скорость v на 50 шаге Рис. 8.18. Скорость v на 300 шаге

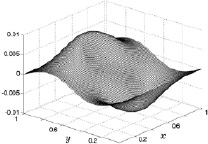
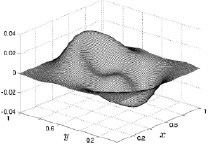
Рис. 8.19. Скорость v на 3000 шаге Рис. 8.20. Скорость v на 10000 шаге

Характер поведения y-й компоненты скорости газа полностью аналогичен поведению x-й компоненты скорости газа, с той лишь разницей, что она описывает движение газа вдоль оси y. В результате, несмотря на принятую в расчетах прямоугольную систему координат, поведение первых двух компонент скоростей таково, что оно соответствует движению газа для принятой изначально центральной кольцевой схеме нагрева подстилающей поверхности. Нестационарный конвективный поток в условиях действия силы тяжести при такой схеме нагрева сохраняет центральную симметрию.

Это хорошо видно на приведенных далее рис. 8.21–8.24 с изображениями поверхностей z-й компоненты скорости газа на той же высоте z = 0,5 (размерное значение 5 м) для четырех фиксированных расчетных шагов по времени. В начальные моменты времени нагрева (рис. 8.21) вертикальная составляющая скорости газа имеет кольцевой характер с малыми значениями 5∙10–8 (размерное 1,67∙10–5 м/с) и фоновыми значениями, равными нулю. На 300 расчетном шаге по времени (рис. 8.22) фоновые значения вертикальной скорости по-прежнему близки к нулю, а кольцеобразная структура размывается в пространстве. При этом безразмерные значения вертикальной скорости достигают 10–3 (размерное 0,333 м/с). С 2000 расчетного шага по времени фоновые значения вертикальной компоненты скорости становятся отрицательными и на 3000 расчетном шаге (рис. 8.23) становятся равными –0,015 (размерное – 5 м/с). В центре расчетной области значения вертикальной скорости также отрицательные, но имеют куполообразную форму со значениями, близкими к нулю. Такое пространственное распределение значений вертикальной составляющей скорости говорит о том, что движение газа с 2000 расчетного шага по времени направлено вертикально вниз и скорость этого движения больше на периферийных участках и меньше в центральной части расчетной области. Далее, с течением времени, происходит дальнейший рост абсолютного значения вертикальной составляющей скорости газа вплоть до значений –0,07 (размерное – 23,3 м/с) на периферии и практически нулевых значениях в центре расчетной области на 10000 расчетном шаге по времени (рис. 8.24).

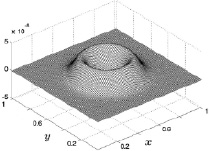
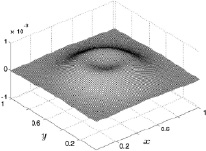
Рис. 8.21. Скорость w на 50 шаге Рис. 8.22. Скорость w на 300 шаге

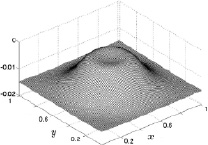
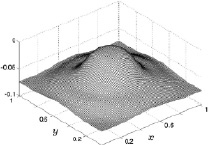
Рис. 8.23. Скорость w на 3000 шаге Рис. 8.24. Скорость w на 10000 шаге

По найденным во внутренних узлах расчетной сетки компонентам скорости и плотности можно рассчитать безразмерное значение энергии движения газа в каждый фиксированный момент времени в расчетной области D.

В работе была рассчитана полная кинетическая энергия W конвективного потока, учитывающая все три компоненты вектора скорости частиц газа

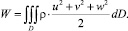(8.5)

На приведенном далее рис. 8.25 представлен результат расчета этой энергии за фиксированный промежуток времени от начала нагрева.

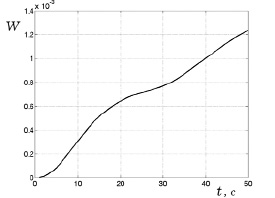
Рис. 8.25. Полная кинетическая энергия

Интерпретация представленной на рис. 8.25 зависимости кинетической энергии от времени является следующей. В начальные расчетные моменты времени поведение кинетической энергии описывается квадратичной функцией скорости. Затем за счет вовлечения в конвективный поток все больших масс газа подводимого количества тепла при нагреве оказывается недостаточно для увеличения скорости его частиц. На графике это фиксируется
как замедление роста кинетической энергии. При дальнейшем нагреве опять наблюдается рост скоростей и кинетической энергии конвективного потока.

И, наконец, приведены результаты расчетов и построений линий тока, дающие возможность визуально представить возникающий в данных условиях конвективный поток. Показано, что по мере возрастания времени нагрева существенным образом меняются и линии тока, показывающие траектории движения частиц газа в конвективном потоке.

На рис. 8.26–8.33 представлены результаты расчета линий тока газа для восьми расчетных шагов по времени. На всех представленных рисунках изображены линии тока конвективного течения газа, выпущенные с плоскости z = 0. Количество линий тока на всех рисунках одинаковое и составляет 10∙10 = 100. В первой серии из четырех рисунков (рис. 8.26–8.29) представлены линии тока, соответствующие возрастанию геометрических размеров конвективного потока в зависимости от расчетного шага по времени, а во второй серии рисунков (рис. 8.30–8.33) изображены линии тока, соответствующие уменьшению геометрических размеров потока.

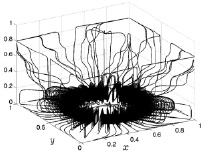
Рис. 8.26. Линии тока на 500 шаге Рис. 8.27. Линии тока на 1000 шаге

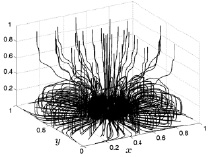
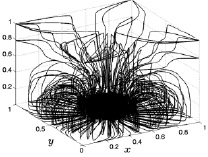
Рис. 8.28. Линии тока на 1500 шаге Рис. 8.29. Линии тока на 2000 шаге

При анализе построенных численно линий тока, представленных на рисунках, можно сделать следующие замечания относительно возникающего конвективного потока. К 500 расчетному шагу по времени (рис. 8.26) линии тока в основном сосредоточены над источником кольцеобразного нагрева в виде тора, имеют значительную густоту и занимают часть пространства по высоте до 0,2 (размерное значение до 2 м). Некоторые линии тока вырываются из кольцеобразного образования, и, имея волнистый характер, доходят до высоты 0,8 (размерное значение 8 м) и далее распространяются вдоль боковых граней расчетного куба.

С точки зрения движения газа как сжимаемой сплошной среды такое поведение линий тока к данному моменту расчетного времени означает формирование тороидального конвективного потока газа большой интенсивности вблизи источника нагрева подстилающей поверхности. Незначительная часть потока газа доходит до боковых граней на высоте 8 м и движется вдоль них. Тот факт, что конвективный поток в основном расположен вблизи подстилающей поверхности и небольшая часть его поднимается до высоты 8 метров, говорит о том, что прогрев основной части изолированного резервуара еще незначительный и конвективный поток не может преодолеть влияние силы тяжести.

Изменения в поведении построенных в результате расчетов линий тока к 1000 расчетному моменту времени (рис. 8.27) сводятся к следующему. При сохранении тороидального характера линий тока, они стали занимать большую часть расчетного пространства, доходя до боковых граней и поднимаясь на высоту 0,3 (размерное значение 3 м). В центре расчетной области возникает вертикальный столб, состоящий из нескольких линий тока, который доходит до верхней грани и далее радиально распространяется вдоль нее до боковых граней. Небольшая часть линий тока, вырывающаяся из тороидального конвективного потока, по-прежнему достигает боковых граней, но теперь поднимаются до верхней грани.

Поскольку прогрев к этому моменту расчетного времени существенно увеличился, то конвективный поток, захватывая все большие слои газа, увеличивается в размерах. Температура в кольце нагрева возрастает до значений, достаточных для преодоления силы тяжести вертикальным конвективным потоком.

Линии тока, построенные для 1500 расчетного шага по времени (рис. 8.28) и для 2000 расчетного шага по времени (рис. 8.29), продолжают тенденции в развитии конвективного потока. Все большие области газа вовлекаются в интенсивное конвективное движение. Высота его к 2000 шагу по времени достигает 0,6 (размерное значение 6 м). Все большее количество линий тока через центральный столб доходит до верхней грани, а затем устремляются к вертикальным ребрам расчетного куба.

Что касается второй серии рисунков (рис. 8.30–8.33), то на них изображены линии тока, соответствующие уменьшению геометрических размеров потока. Из результатов расчетов видно, что при сохранении большой
интенсивности (густота линий тока) линейные размеры конвективного потока постепенно уменьшаются с течением времени и к 4000 шагу достигает высоты 0,2 (размерное значение 2 м) и радиуса 0,2 (размерное 2 м).

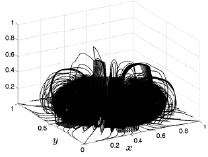
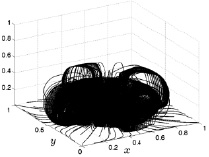
Рис. 8.30. Линии тока на 2500 шаге Рис. 8.31. Линии тока на 3000 шаге

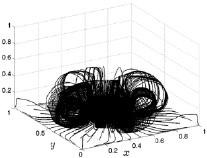
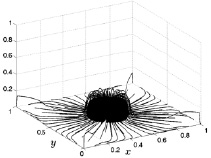
Рис. 8.32. Линии тока на 3500 шаге Рис. 8.33. Линии тока на 4000 шаге

Такое поведение конвективного течения газа объясняется, по-видимому, тем, что повышение температуры приводит к повышению давления в расчетном объеме и, как следствие, к сокращению размеров области движения газа.

Для описания нестационарных трехмерных конвективных течений вязкого сжимаемого теплопроводного газа в замкнутой кубической области рассмотрено численное решение полной системы уравнений Навье – Стокса. Коэффициенты вязкости и теплопроводности полагаются постоянными. За начальные условия принимаются функции, являющиеся точным аналитическим решением полной системы уравнений Навье – Стокса. В качестве краевых условий предлагаются условия непротекания и теплоизоляции.

Возникающий при кольцеобразном нагреве нижней грани расчетной области конвективный поток газа в условиях действия силы тяжести имеет ярко выраженный нестационарный характер, более отчетливо проявляющийся в начальной стадии его формирования.

Прежде всего, это касается термодинамических характеристик – температуры, плотности и давления. Показано, что термодинамические параметры имеют сложную структуру и существенным образом зависят от формы нагрева, высоты и времени нагрева.

Рассчитаны три компоненты вектора скорости для начальной стадии формирования конвективного потока и показано, что компоненты скорости имеют также сложную структуру и существенным образом зависят от формы нагрева, высоты и времени нагрева.

Построенные линии тока частиц газа показывают, что течения сжимаемого теплопроводного газа в условиях теплоизоляции и непротекания имеют сложный характер. Показано, что конвективное течение газа в начальной стадии его формирования существенно зависит от формы нагревательного элемента, температуры и времени нагрева.

Численное решение в нестационарном случае полной системы уравнений Навье – Стокса с корректно поставленными начальными и краевыми условиями позволяет сделать вывод о том, что предложенная вычислительная схема работает корректно, начальные и краевые условия адекватны исследуемым течениям газа, возникающим в результате кольцевого нагрева, и результаты расчетов получаются понятными с физической точки зрения. Дальнейшая работа в этом направлении может быть связана с продолжением расчета конвективных течений газа для больших расчетных шагов по времени.