Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

8.1. Применение дробного дифференцирования для описания структуры полимерных расплавов

Как показано в работе [1], уравнения в дробных производных описывают эволюцию некоторой физической системы с потерями, причем дробный показатель производной указывает на долю состояний системы, сохраняющихся за все время эволюции t. Такие системы могут быть классифицированы как системы с «остаточной» памятью, занимающие промежуточное положение между системами, обладающими полной памятью, с одной стороны, и марковскими системами, с другой. Очевидно, что фрактальная структура полимеров является именно такой промежуточной системой, часть которой теряется в процессе термоокислительной деструкции (см. уравнения (6.1) ¸ (6.3)). В рамках дробного интегро-дифференцирования удается последовательно учесть сложную природу нелинейных явлений, таких, как эффекты памяти и пространственные корреляции [2]. При этом не только воспроизводятся ранее известные решения, но и дается их нетривиальное обобщение. Еще одна важная особенность связана со свойством самоподобия фрактальных структур. В отличие от традиционных способов описания системы на основе различных процедур усреднения, когда происходит «стирание» микроскопического уровня, в концепции фрактала учитывается самоаффинная структура среды и тем самым в рамках концепции фрактала объединяются микроскопический и макроскопический уровни описания системы. Именно такой способ важен для сложных многокомпонентных систем, находящихся далеко от состояния термодинамического равновесия [2].

Нигматуллин [1] указал, что хотя математический аппарат дробного исчисления в настоящее время хорошо разработали [3; 4], широкое применение дробных интегралов и производных сдерживается по одной простой причине - отсутствием у них ясной физической интерпретации. Если найти их четкое физическое истолкование, примерно такое же, какое существует у обыкновенного интеграла и производной, то оно несомненно бы расширило область их применения в физике. Именно этот аспект применения дробного дифференцирования является ключевым в настоящей главе.

Как известно [5], кинетические кривые окисления  автозамедленного типа, экспоненциально убывающие во времени, описываются следующим эмпирическим уравнением:

,                                     (8.1)

где  - предельное количество кислорода, способное поглотиться при окислении, k_d - эффективная константа скорости окисления, t - время.

Зависимость (8.1) обычно объясняется неоднородностью структуры полимера, которая определяет заметные различия в скоростях окисления отдельных ее участков. Поскольку более реакционноспособные участки окисляются в первую очередь, после их практически полного превращения скорость суммарного процесса сильно снижается. Кроме того, было показано, что величина , определяемая с помощью формулы (8.1) может быть во много раз ниже концентрации мономерных звеньев в индивидуальном полимере: во время опыта некоторая часть этих звеньев ведет себя как инертное вещество [6].

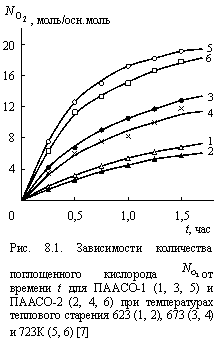
Значение k_d зависит от температуры и структуры полимера [5]. Как отмечалось выше, из сказанного следует, что по существу и , и k_d являются просто подгоночными параметрами, поскольку их количественное соотношение со структурой полимера не выяснено. Поэтому авторы работ [7; 8] предприняли попытку выяснить структурный смысл указанных параметров на примере двух блок-сополимеров ПААСО (ПААСО-1 и ПААСО-2, см. табл. 6.1) при трех температурах теплового старения.

Напомним физические основы применения математического аппарата дробного дифференцирования для описания структуры полимерного расплава или, точнее, структуры макромолекулярного клубка, характеризуемой ее фрактальной размерностью D_f [9]. Из приведенного в предыдущих главах обсуждения следует, что в случае автозамедленного режима окисления процесс термоокислительной деструкции для рассматриваемых блок-сополимеров протекает не в евклидовом, а во фрактальном пространстве с размерностью D_f [10]. В этом случае процесс деструкции схематически можно представить в виде «чертовой лестницы» [11]. Ее горизонтальные отрезки соответствуют временным интервалам, где реакция не идет. Такой процесс деструкции описывается с использованием фрактального времени t, которое принадлежит точкам канторова множества [12]. Если же реакция рассматривается в евклидовом пространстве, то время принадлежит множеству действительных чисел.

Для описания эволюционных процессов с фрактальным временем используется математический аппарат дробного дифференцирования и интегрирования [12]. Как показано в работе [1], в этом случае дробный показатель n_d совпадает с фрактальной размерностью множества Кантора и указывает на долю состояний системы, сохраняющихся за все время эволюции t. Напомним, что множество Кантора рассматривается в одномерном евклидовом пространстве (d = 1) и поэтому его фрактальная размерность d_f < 1 в силу определения фрактала [11]. Для фрактальных объектов в евклидовых пространствах с более высокими размерностями (d > 1) в качестве n_d следует принимать дробную часть d_f (в нашем случае - D_f) согласно уравнению (6.1). Тогда величина n_d характеризует долю фрактала (макромолекулярного клубка), сохраняющуюся в процессе деструкции. Очевидно, доля макромолекулярного клубка b_d, распадающаяся в процессе деструкции, определяется как (1 - n_d) и рассчитывается согласно уравнениям (6.2) и (6.3).

Далее естественно предположить, что кислород поглощается в части макромолекулярного клубка, распадающейся в процессе термоокислительной деструкции. Тогда, рассчитав величину , необходимую для окисления всех метильных и алифатических групп ПААСО (которая, как и ранее, принята равной 24,1 моль О₂/осн. моль полимера), можно определить параметр   следующим образом [7]:

.                                                    (8.2)

Изменение D_f означает изменение степени компактности макромолекулярного клубка [13]. Как было показано ранее, снижение D_f, определяющее уменьшение компактности клубка, приводит к росту  и, следовательно, k_d, что позволяет заменить k_d структурным параметром [8]. Охарактеризовать степень компактности макромолекулярного клубка можно с помощью его плотности r, определяемой согласно соотношению (2.22). Для простоты авторы [7; 8] приняли R_g = 100 отн. ед. (величины  для ПААСО-1 и ПААСО-2 близки, см. табл. 6.1) и плотность r определяли из следующего уравнения для обоих блок-сополимеров и всех температур теплового старения:

,                                                   (8.3)

где коэффициент 8,2 выбран эмпирически.

Теперь уравнение (8.1) с учетом рассмотренных структурных факторов может быть записано так [7]:

.                           (8.4)

Показатель экспоненты -(t/r) записан в такой форме потому, что действие r противоположно действию t: увеличение r снижает поглощение кислорода и наоборот. На рис. 8.1 показаны экспериментальные зависимости  для обоих рассматриваемых блок-сополимеров и трех температурах теплового старения. Как можно видеть, все кинетические кривые  относятся к автозамедленному типу:  экспоненциально убывает во времени. Это означает уменьшение скорости поглощения кислорода   cо временем t. Такое поведение   однозначно указывает на протекание процесса термоокислительной деструкции во фрактальном пространстве [14].

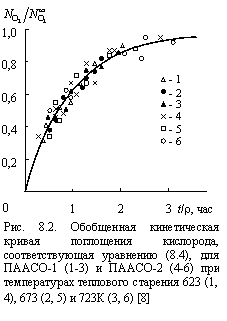
На рис. 8.2 показана обобщенная кинетическая кривая поглощения кислорода для ПААСО-1 и ПААСО-2 при трех температурах теплового старения. Как можно видеть, экспериментальные результаты хорошо описываются уравнением (8.4), не содержащим эмпирических коэффициентов.

Следовательно, изложенные выше результаты показали необходимость применения методов фрактального анализа и дробного дифференцирования для описания кинетики процессов термоокислительной деструкции полимерных расплавов. Основным постулатом, принципиально отличающимся от представлений классических моделей является деструкция только части макромолекулярного клубка, определяемой его структурой. Кинетика поглощения кислорода определяется химическим строением полимера  и его структурой (D_f и r) [7; 8].

Отметим важную общую особенность всех трех рассмотренных выше методов структурного описания термоокислительной деструкции [7; 9; 14]. Все они тем или иным способом учитывают неоднородность структуры полимерного расплава. Так, фрактальная (Хаусдорфова) размерность D_f определяет изменение плотности r фрактала (макромолекулярного клубка) или распределение его элементов в пространстве как функцию его размера R_g согласно соотношению (2.22) [13].

Дробный показатель n_d характеризует неоднородность структуры макромолекулярного клубка, определяя ту его часть, которая не подвергается окислению в процессе термоокислительной деструкции. И, наконец, эффективная спектральная размерность  является однозначной функцией показателя неоднородности h согласно уравнению (1.69).

Следовательно, все три предложенных метода в том или ином варианте учитывают неоднородность структуры расплава полимера, которая определяет ход процесса его термоокислительной деструкции [9].

В настоящее время принято считать, что число реакционноспособных центров полимерной макромолекулы, способных реагировать с молекулами оксиданта, определяется химическим строением полимера [6]. Однако, полимерная макромолекула как в растворе, так и в конденсированном состоянии представляет собой макромолекулярный клубок, который является фрактальным объектом [15]. Характерной особенностью фрактальных структур является разная степень доступности их элементов в разных областях фрактала: на поверхности фрактала она гораздо выше, чем в его внутренних (экранированных поверхностью) областях [16]. Поэтому следует предположить, что эффективное число реакционноспособных мест полимерной макромолекулы определяется не только (и, возможно, не столько) ее химическим строением, но и структурой макромолекулярного клубка. Авторы работ [17-19] определили влияние структуры макромолекулярного клубка на эффективное число реакционноспособных мест макромолекулы на примере расплава ПААСО, полученных разными способами поликонденсации, с привлечением методов фрактального анализа, скейлингового подхода и аппарата дробного дифференцирования [20; 21].

Согласно [22] константа А в соотношении (6.12) пропорциональная концентрации ловушек (реакционноспособных центров макромолекул). Тогда зависимости c(t) » exp(-At) в двойных логарифмических координатах, подобные приведенным на рис. 6.19, позволяют определить величины А для ПААСО [17].

На рис. 8.3 приведена зависимость А(D_f) для ПААСО (условные обозначения даны в табл. 6.1). Как и следовало ожидать, увеличение D_f или повышение степени компактности макромолекулярного клубка приводит к снижению А или уменьшению эффективного числа реакционноспособных центров макромолекул ПААСО. Подавляющая часть этих центров находится во внутренних областях макромолекулярного клубка и при D_f » 2,8 доступ оксиданта в эти области экранируется его поверхностью, т.е., в этом случае окислению могут подвергаться только те реакционноспособные центры макромолекулы, которые расположены на поверхности клубка [18]. Это обстоятельство подтверждает структурный критерий изменения типа кинетических кривых, подробно рассмотренный в разделе 7.1.

Можно предположить, что величина А или эффективное число реакционноспособных центров макромолекулы пропорциональна доле макромолекулярного клубка, подвергающейся деструкции или (1-n_d) для ПААСО, которая оказалась линейной, и величина А при (1-n_d) » 0,21 или D_f » 2,79 достигает примерно постоянного значения, небольшого по абсолютной величине: А » 0,04 (см. также раздел 7.1). Эта величина А согласуется с реакцией оксиданта только по поверхности макромолекулярного клубка. Для D_f < 2,80 можно записать аналитическое соотношение между А и n_d [18]:

A = 0,5(4 - 5n_d),                                                 (8.5)

и тогда с учетом уравнений (6.10 и (6.12) получим [19]:

Q = 1 - exp[- 0,5(4 - 5n_d)t].                            (8.6)

Из уравнения (8.6) следует, что при n > 0,8 изменяется механизм термоокислительной деструкции, поскольку показатель в этом уравнении становится положительным [17].

Таким образом, приведенные выше данные показали, что эффективное число реакционноспособных центров полимерной макромолекулы зависит от структуры макромолекулярного клубка. Количественную характеристику последней можно получить в рамках представлений фрактального анализа и дробного дифференцирования. Увеличение фрактальной размерности макромолекулярного клубка, означающее повышение степени его компактности, приводит к снижению эффективного числа реакционноспособных (доступных для молекул оксиданта) мест полимерной макромолекулы [17-19].

Авторы [23] предположили, что в твердофазных полимерах всегда имеет место анизотропия по структурным характеристикам. Поэтому они ввели термин доступности связей полимера для протекания тех или иных реакций. Кроме того, они показали, что при учете доступности скорость гидролиза амидных связей и растворимость воды в полиамиде-12 не зависят от структуры образца.

Применение методов фрактального анализа для описания структуры и свойств полимеров позволяет предположить, что понятие «доступности» структуры полимеров для реализации тех или иных процессов касается не только твердофазного, но и любого другого состояния полимеров [7; 9; 17]. Это явление имеет фундаментальную причину - фрактальную природу структуры полимеров. Для подтверждения этого положения авторы [24] дали теоретическое структурное определение «доступности» и продемонстрировали его применение для описания термоокислительной деструкции расплавов поликарбоната.

На рис. 7.1 приведены зависимости числа разрывов s на макромолекулу от продолжительности теплового старения t_ст для пленок ПК, полученных из растворов в хлороформе и хлористом метилене (пленки ПК, полученные из растворов в хлористом метилене и хлорбензоле, имеют очень сходные кривые s(t_ст), перекрывающие друг друга, и поэтому данные для последних на рис. 7.1 не показаны). Как можно видеть, эти кинетические кривые s(t_ст) относятся к смешанному s-образному типу кинетических кривых, где на начальном участке (до t_ст £ 6 час.) наблюдается режим автоускорения, при t_ст ³ 7,5 час., переходящий в автозамедленный режим, и при t_т ³ 9 час. происходит выход кинетической кривой s(t_ст) на асимптотическую ветвь [5]. Обращает на себя внимание тот факт, что указанный выход реализуется при разных значениях t_ст для одного итого же полимера (в данном случае - ПК). Это означает, что разная структура пленок ПК, полученных из разных растворителей, сохраняется и в расплаве полимера, о чем говорят и разные значения D_f для них (см. табл. 7.1).

В работе [23] было предложено следующее уравнение для расчета экспериментальных значений характеристической вязкости [h]_эксп:

[h]_эксп = [h]₁f₁ + [h]₂f₂,                                        (8.7)

где [h]₁ и [h]₂ - характеристические вязкости, а f₁ и f₂ - весовые доли соответственно доступной и недоступной для окисления фаз. При этом предполагается, что [h]₂ » [h]₀, где [h]₀ - характеристическая вязкость исходного полимера.

Характеристическая вязкость [h] представляет собой комплексную характеристику, которая зависит от структуры макромолекулярного клубка в растворе и молекулярной массы ММ довольно сложным способом [25]. Поскольку уравнение (8.7) по существу представляет собой хорошо известное правило смесей [12], то авторы [24] заменили в нем величины [h] на соответствующие молекулярные массы полимера ММ_эксп = М_h, где М_h рассчитана по уравнению Марка-Куна-Хаувинка [26], ММ₁ и ММ₂ и ММ₀. Кроме того, полагая, что f₂ равно дробному показателю n_d или f₁ = (3 - D_f), авторы [24] заменили параметры f₁ и f₂ на соответствующие структурные характеристики (3 - D_f) и (D_f - 2). Тогда уравнение (8.7) принимает следующий вид [24]:

ММ_эксп = (3 - D_f)MM₁ + (D_f - 2)MM₀.             (8.8)

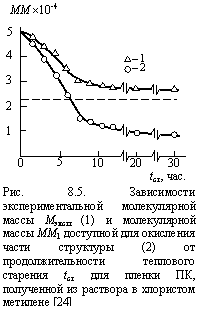
На рис. 8.5 приведены зависимости ММ_эксп и ММ₁ от продолжительности теплового старения t_ст, а штриховой горизонтальной линией показано предельное значение молекулярной массы, которое может быть достигнуто полимером в процессе деструкции, равное    (D_f - 2)ММ₀. Как следует из данных этого рисунка, при t_ст ³ 9 час величина ММ_эксп асимптотически приближается к предельному значению ММ (при t_ст = 12 час. расхождение составляет ~ 22 %), а величина ММ₁ так же асимптотически стремится к нулю. Экстраполяция ММ₁ к нулю показала, что это значение должно быть достигнуто при t_ст » 80 час. Для проверки этого предположения было выполнено тепловое старение пленок ПК, полученных из раствора в хлористом метилене, при Т_ст = 513 К для t_ст = 20 и 30 час. Эти испытания показали, что при t_ст = 20 час. величина ММ₁ действительно снижается на 14 % по сравнению с ММ₁ при t_ст = 12 час., а при t_ст = 30 час. - на 7 % по сравнению с ММ₁ при t_ст = 20 час., т.е., наблюдается медленное асимптотическое приближение ММ₁ к нулю.

Если предположить, что ПК в доступной для окисления части структуры подвергается термоокислительной деструкции независимо от своего структурного состояния, т.е., величины D_f, то значения ММ₁ должны быть одинаковы для всех исследуемых пленок ПК. Для проверки этого предположения авторы [46] рассчитали величины ММ₁ для пленок ПК, полученных из раствора в хлористом метилене, согласно уравнению (8.8) и затем согласно этому же уравнению оценили величины ММ₁ для пленок ПК, полученных из растворов в хлороформе и хлорбензоле, с использованием этих значений ММ₁. Сравнение зависимостей ММ_эксп(t_ст) и ММ_т(t_ст) для двух последних пленок приведено на рис. 8.6 (на этом рисунке приведена только одна зависимость ММ_т(t_ст) поскольку для указанных пленок ПК расчет ММ_т по уравнению (8.8) дает близкие значения). Как можно видеть, получено достаточно хорошее соответствие теории и эксперимента (среднее расхождение 13,9 % для пленок, полученных из раствора в хлороформе, и 5,8 % - из раствора в хлорбензоле). Более высокая погрешность для первых из указанных пленок, вероятно, обусловлена погрешностью в оценке D_f. Тем не менее, данные рис. 8.6 предполагают корректность допущения постоянной скорости термоокислительной деструкции доступной для этого процесса части полимера, не зависящей от структуры расплава.

Следовательно, изложенные выше данные продемонстрировали, что «доступность» полимера для окисления является чисто структурным фактором и количественно оценивается в рамках теории дробного дифференцирования. Скорость окисления «доступной» части макромолекулярного клубка не зависит от его структуры, что позволяет предположить ее зависимость только от химического строения полимера [24].