Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОПТИМАЛЬНАЯ ОБРАБОТКА РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ, ФОРМИРУЕМЫХ В РСА

Доросинский Л. Г.,

2.10.4. Аппроксимации путем разложения в ряд

Все описанные до сих пор непараметрические методы имеют тот недостаток, что требуют хранения в памяти всех выборок. А так как для получения хороших оценок необходимо большое количество выборок, то потребность в памяти может быть слишком велика. Кроме того, может потребоваться значительное время вычисления каждый раз, когда один из методов используется для оценки величины р(x) или классификации нового x. При определенных обстоятельствах процедуру окна Парзена можно несколько видоизменить, чтобы значительно сократить эти требования.

Основная идея заключается в аппроксимации функции окна путем разложения ее в конечный ряд, что делается с приемлемой точностью в представляющей интерес области. Если нам сопутствует удача и мы можем найти два множества функций φ_j(x) и Φ_j(x), которые допускают разложение

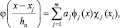(2.10.9)

тогда

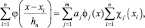
и из уравнения (2.10.6) имеем

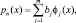
где 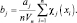(2.10.10)

Этот подход имеет некоторые преимущества в том случае, когда можно получить достаточно точное разложение с приемлемым значением m. Информация, содержащаяся в n выборках, сводится к m коэффициентам b_j. Если получают дополнительные выборки, соотношение (2.10.10) для bj можно легко обновить, причем количество коэффициентов остается неизменным.

Если функции ψ_j и χ_j являются полиномами от компонент x и x_i, то выражение для оценки p_n(x) есть также полином, который можно довольно эффективно вычислить. Более того, использование этой оценки для получения разделяющих функций p(x/H_i), P(H_i) приводит к простому способу получения полиномиальных разделяющих функций.

Следует отметить одну из проблем, возникающую при применении этого способа. Основным достоинством функции окна является ее тенденция к возрастанию в начале координат и снижению в других точках, так что 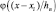будет иметь резкий максимум при x = x_i и мало влиять на аппроксимацию p_n(x) для удаленного от x_i. К сожалению, полиномы обладают досадным свойством, заключающимся в том, что они могут содержать неограниченное количество членов. Поэтому при разложении полинома могут обнаружиться члены, ассоциируемые с x_i, удаленным от x, сильно влияющим на разложение. Следовательно, важно убедиться, что разложение каждой функции окна действительно точное в представляющей интерес области, а для этого может потребоваться большое число членов.

Существует много видов разложения в ряд. Читатели, знакомые с интегральными уравнениями, вполне естественно интерпретируют соотношение (2.10.9) как разложение ядра φ(x, x_i) в ряды по собственным функциям. Вместо вычисления собственных функций можно выбрать любое приемлемое множество функций, ортогональных в интересующей нас области, и получить согласие по методу наименьших квадратов с функцией окна. Мы применим еще более непосредственный подход и разложим функцию окна в ряд Тейлора. Для простоты ограничимся одномерным случаем с гауссовской функцией окна:

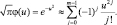
Самым точным это разложение будет в окрестности u = 0, где ошибка будет составлять менее u^2m/m!. Если мы подставим 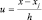, то получим полином степени 2(m – 1) от x и x_i. Например, если m = 2, то

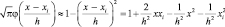
и, таким образом,

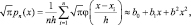
где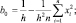

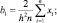
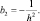
Это простое разложение сжимает информацию из n выборок в три коэффициента b0, b1, b2. Оно будет точным, если наибольшее значение | x – x_i | не превышает h. К сожалению, это заставляет нас пользоваться очень широким окном, которое не дает большого разрешения. Беря большое количество членов, мы можем использовать более узкое окно. Если мы считаем r наибольшим значением |x – x_i|, то, пользуясь тем фактом, что ошибка в m-членном разложении функции 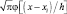меньше, чем (r/h)^2m m!, и пользуясь аппроксимацией Стирлинга для m!, найдем, что ошибка в аппроксимации p_n(x) будет меньше, чем

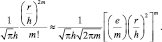
Таким образом, ошибка мала только тогда, когда m > e(r/h)². Это говорит о том, что требуется много членов, если ширина окна h невелика по сравнению с расстоянием r от x до наиболее удаленной выборки.