Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОПТИМАЛЬНАЯ ОБРАБОТКА РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ, ФОРМИРУЕМЫХ В РСА

Доросинский Л. Г.,

3.3. Квазиоптимальные и эмпирические алгоритмы классификации ПРЦ

В предыдущих разделах описан алгоритм формирования достаточной статистики и получения на её основе признаков классификации ПРЦ при точно известных параметрах, характеризующих взаимное расположение и особенности взаимного перемещения ПРЦ и КА. В реальных условиях с достаточно высокой точностью могут быть известны лишь некоторые из этих параметров, в первую очередь, относящиеся к описанию движения носителя РЛС. Ряд параметров, необходимых для решения задачи распознавания, может быть с достаточной точностью оценен на этапе обнаружения ПРЦ. В частности, в процессе обнаружения могут быть оценены положение центра цели и величина ее радиальной скорости. Вместе с тем, ряд параметров, играющих основную роль для эффективного распознавания (например, ракурс цели и ее угловая скорость вращения), к моменту решения задачи классификации остаются неизвестными.

Объединим параметры, описывающие ракурсы наблюдения цели всеми РЛС системы, в вектор , а из оставшихся параметров выделим вектор известных и неизвестных параметров. При этом оптимальный в смысле максимального правдоподобия алгоритм классификации требует определения логарифмов отношения правдоподобия Ik [(U(t))/(Χ₀, Χ, ν)] для всех возможных значений векторов неизвестных параметров и всех классов целей. Процедура нахождения логарифма отношения правдоподобия строится в соответствии с алгоритмом, описанным в разделе 3.1. Основная процедура такого алгоритма заключается в формировании радиолокационного изображения наблюдаемого объекта в системе координат, связанной с геометрическими осями цели, для всех возможных сочетаний параметров Χ и ν в соответствии с выражением

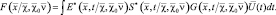(3.3.1)

На этапе получения РЛИ знание вектора ракурсов необходимо для задания ориентации осей вспомогательной системы 0xyz в пространстве. Этот факт позволяет использовать для распознавания изображения, построенные в предположении о совпадении ориентации осей вспомогательной и основной систем координат. Учет истинного положения осей ПРЦ может быть выполнен при формировании статистики .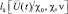

Практическая реализация оптимальных и близких к ним алгоритмов наталкивается на многочисленные трудности, связанные, в первую очередь, с отсутствием необходимой априорной информации о характеристиках отражающих свойств наблюдаемых объектов, характеристиках их движения относительно координатной системы, связанной с ПРЦ. Действительно, оптимальные алгоритмы требуют знания распределения «блестящих точек» (центров отражения) по координатам поверхности корабля при всех возможных на практике условиях наблюдения (изменяющиеся ракурсы, угловые скорости вращения относительно осей ПРЦ, индивидуальные особенности постройки ПРЦ).

Названные соображения вызывают повышенный интерес к поиску более простых и одновременно достаточно эффективных способов классификации ПРЦ. При этом, по-прежнему, определяющим является выбор классификационных признаков, поскольку выбор решающих правил существенно зависит от номенклатуры и свойств этих признаков.

Выше показано, что в рамках типовых ограничений, связанных с априорной неопределённостью о большинстве параметров движения ПРЦ, в качестве вектора признаков целесообразно выбирать вектор следующего вида:

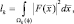
где k меняется от 1 до числа классов М.

Дальнейшее упрощение может быть связано с отказом от использования вектора признаков, размерность которого равна числу распознаваемых классов, и переходом к скалярной величине, равной суммарной ЭПР РЛИ, полученной интегрированием по области изображения, в пределах которой отсчеты РЛИ превышают некоторый порог F, устанавливаемый, например, адаптивно по величине оцененной ЭПР подстилающей поверхности, «не занятой» целью.

Указанный признак может быть получен в соответствии с выражением

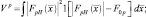(3.3.2)

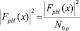(3.3.3)

– нормированное к величине ЭПР водной поверхности и шума РЛИ наблюдаемой цели; 1[·] – функция Хевисайда.

Признак Vp может быть условно назван «объемом РЛИ». Ещё более простой признак формируется из «объема» при замене квадратов модуля РЛИ единицами. Такой признак по существу представляет собой оценку площади РЛИ ПРЦ при заданном пороге F:

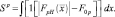(3.3.4)

Для целей, отношение длины которых к ширине примерно одинаково, вместо площади РЛИ может быть использована оценка длины ПРЦ, определяемая по формуле

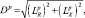(3.3.5)

где 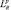и 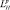– длины РЛИ, формируемого р-й РЛС, по дальности и азимуту.

Очевидно, что каждая из величин, входящая в (3.3.5) может рассматриваться как признак, используемый для классификации.

Описанные признаки V p, S p, D p, 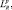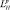называются в дальнейшем геометрическими. При их использовании решение в общем случае выносится по данным всех Р РЛС. Такой способ принятия решения отрицательно сказывается на автономности функционирования каждой отдельной радиолокационной станции. Поэтому при независимости входящих в систему станций целесообразно выносить частное решение каждой отдельной РЛС с последующим объединением решений методами «голосования» [6].

Рассмотрим другую группу признаков. Отказываясь от детальной обработки РЛИ (в связи с упомянутым выше отсутствием достаточных априорных сведений), сохраним в качестве основной исходной информации РЛИ наблюдаемой цели в виде квадрата модуля комплексного изображения: 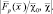Один из путей построения системы признаков в этом случае заключается в использовании собственно отсчетов формируемого РЛИ. Для сокращения размерности вектора признаков можно воспользоваться различными функционалами, построенными на пространстве признаков, в частности, моментами РЛИ, которые были предложены для модели зрительного восприятия человека в 60-х годах [3]. Вычисление начального момента r + q-гo порядка осуществляется в соответствии с выражением

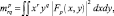(3.3.6)

где х и у – координаты РЛИ.

Моменты (3.3.6) представляют собой не что иное, как коэффициенты в разложении спектральной плотности РЛИ в ряд Тейлора. Отсюда следует, что выбор достаточного числа моментов позволяет описать РЛИ с любой наперед заданной точностью. В то же время наиболее существенными и информативными являются моменты относительно невысоких порядков, что позволяет существенно сократить размерность вектора признаков по сравнению с исходным числом отсчетов формируемого РЛИ.

Использование моментов в качестве признаков привлекательно еще и из тех соображений, что на их основе могут быть построены инварианты к афинным преобразованиям (сдвиг, поворот и изменение масштаба). Следует, однако, иметь в виду, что создание инвариантов ко всем видам возможных искажений РЛИ принципиально не представляется возможным [7], поскольку при изменении ракурса наблюдения, например, меняется содержание РЛИ, а не его геометрические характеристики.

Поскольку изображение ПРЦ в общем случае сдвинуто относительно центра кадра, представляется целесообразным использовать центральные моменты РЛИ, инвариантные к этому типу искажений:

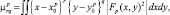(3.3.7)

где 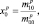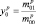– координаты центра тяжести РЛИ.

Следует отметить, что при наблюдении цели в разное время даже при одинаковом ракурсе ее РЛИ могут отличаться на постоянный множитель

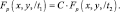(3.3.8)

Источниками названных искажений могут быть: неравномерность ДН антенны РЛС по дальности и изменение коэффициента усиления приемника РЛС во времени за счет АРУ по шумам, регулирующей усиление в зависимости от метеоусловий в районе наблюдения. Для устранения искажений (3.3.8) следует воспользоваться нормированными центральными моментами:

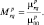(3.3.9)

Для уменьшения влияния шумов на формирование признаков, основанных на вычислении моментов, интегрирование в (2.3.7) следует проводить в пределах области, где модуль РЛИ превышает заранее установленный порог F_0p, т.е.

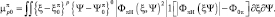(3.3.10)

Обратим внимание на тот факт, что при r = q = 0 (2.3.2) и (2.3.10) совпадают, т.е.

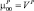. (3.3.11)

Рассмотрим теперь правила вынесения решений, которые могут использоваться для принятия решения о типе наблюдаемого ПРЦ по геометрическим признакам и признакам, основанным на вычислении моментов. Надо сказать, что геометрические признаки требуют для их использования минимальной априорной информации, и в связи c этим являются весьма «грубыми». Любой из этих признаков ставит в соответствие сложному объекту, каким является ПРЦ, одно число, в той или иной степени отражающее размеры цели и ее суммарную ЭПР. Поскольку эффективная поверхность цели существенно зависит от ракурса, а размеры РЛИ определяются как величиной порога, так и условиями наблюдения, в частности, состоянием морской поверхности и, как следствие, уровнем порога, применение геометрических признаков особенно целесообразно при наблюдении группы ПРЦ под одним ракурсом. Таким требованиям удовлетворяет случай слежения за ордером ПРЦ при его движении в одном направлении.

Для каждого ПРЦ из наблюдаемого ордера формируется РЛИ, на основе которого определяется значение одного из геометрических признаков. Для примера будем считать, что этот признак – «объем РЛИ» – V p. В результате получим вектор

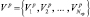
где N_гр – число целей в группе – ордере. Среди компонентов этого вектора определяются наименьшее 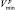и наибольшее 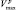значения, которые используются для вычисления двух адаптивных порогов – нижнего

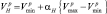
и верхнего

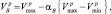
где α_в и α_н – положительные константы.

Решение о принадлежности i-й цели ордера к одному из трех возможных классов выносится путем сравнения V_i с порогам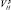и и .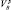

Если 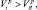то цель относится к классу «больших». При 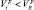наблюдаемая цель относится к классу «малых». Остальные ПРЦ относятся к «среднему» классу.

Моменты РЛИ описывают изображение цели значительно более подробно, поэтому они могут быть использованы для распознавания ПРЦ не только в составе ордера но и по одиночным РЛИ. Решение в этом случае может быть вынесено по сформированному вектору признаков различными способами, пять из которых описаны ниже. Приведенные правила являются наиболее употребительными [8], причем выбор конкретного правила должен производиться в процессе анализа алгоритмов классификации.

Правило 1. Предполагая вектор признаков гауссовским с вектором средних значений М и ковариационной матрицей Н (k – номер класса целей), запишем правило решения по максимуму правдоподобия

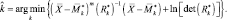(3.3.12)

Правило 2. Это правило отличается от предыдущего тем, что при вычислении квадратичной формы и определителя в (3.3.12) учитываются только диагональные члены ковариационной матрицы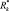

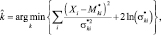(3.3.13)

где X_i, 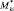– i-е компоненты вектора признаков и средних значений, соответствующие k-й цели; 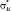– дисперсия i-го компонента вектора признаков для цели k-го класса.

Правило 3 опирается на метод k ближайших соседей, суть которого состоит в следующем. В пространстве признаков вычисляется расстояние от точки, задаваемой вектором X, до каждой из точек классифицированной обучающей выборки. Все точки обучающей выборки ранжируютcя по возрастанию вычисленного расстояния. Вслед за этим выбираются k первых членов ранжированной последовательности (ближайшие соседи) и подсчитывается число соседей, относящихся к каждому из классов. Решение выносится в пользу того класса, к которому относится наибольшее число «ближайших соседей».

Правило 4. В соответствии с этим правилом решение принимается по минимуму эвклидова расстояния в пространстве признаков от точки, заданной вектором X, до точек, определяемых векторами средних значений для каждой цели. При этом решение выбирается в соответствии с алгоритмом

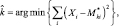(3.3.14)

который является частным случаем правила 2 при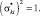

Правило 5. Предусматривает минимизацию среднего расстояния от точки, заданной вектором X до точек обучающей выборки i-го класса. Усреднение производится по всем обучающим выборкам

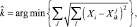(3.3.15)

где 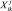– значение i-й компоненты вектора признаков, полученного в j-й реализации обучающей выборки k-го класса.

Следует отметить, что названные правила не исчерпывают всего многообразия возможных способов вынесения решения. Выбор конкретного правила существенным образом зависит от технических возможностей проектируемой системы классификации.

Как правило, статистические характеристики признаков априори неизвестны, поэтому в алгоритмах (3.3.12)–(3.3.15) обычно используются оценки векторов средних значений и ковариационных матриц по обучающим выборкам для каждого из распознаваемых классов.