Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.5. Межобзорная идентификация РЛИ ПРЦ
Решение задачи классификации по одному наблюдению может оказаться недостаточно достоверным вследствие искажений РЛИ, вызванных его флуктуациями и рядом других причин особенно при большой мощности сигнала, отражённого от подстилающей поверхности. В таких случаях эффективность решения задачи может быть повышена за счет применения комплексного распознавания несколькими решающими автоматами (РА).
В связи с тем, что каждый РА содержит в своем банке наблюдаемых данных несколько РЛИ различных целей, возникает проблема их идентификации, иначе говоря, ответа на вопрос, какие конкретные фрагменты, содержащие отметки от целей в каждом из Р различных обзоров, принадлежат одному и тому ПРЦ.
Предположим, что каждое j-е РЛИ, полученное в р-м обзоре, представлено вектором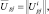 
(
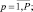
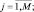
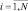), размерность которого N выбрана таким образом чтобы РЛИ ПРЦ наибольшего размера полностью размещалось в пределах заданного фрагмента МП. Нумерация фрагментов, наблюдаемых на радиолокационной карте (содержащихся в банке данных) производится по заданному правилу (в примере, показанном на рис. 4.8 слева – направо, сверху – вниз). При этом общая совокупность РЛИ, подлежащих идентификации, имеет вид:
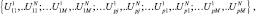(5.5.1)
где первый индекс р – номер обзора; второй индекс j – номер РЛИ в р-м обзоре; третий индекс i – номер отсчета j-гo РЛИ р-го обзора. Пусть j-e РЛИ определено вектором параметров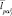 
(
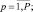
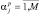), где р – по-прежнему номер обзора, а 
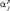– истинный порядковый номер ПРЦ, соответствующего j-му РЛИ в р-м обзоре. Компонентами вектора 
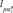являются все доступные для анализа параметры объекта, в частности, статистические характеристики отсчетов РЛИ (математические ожидания, дисперсии и т.п.), траекторные параметры (координаты, скорости поступательного и вращательного движений и т.д.), оценки ЭПР, размеров и т.п.
а
б
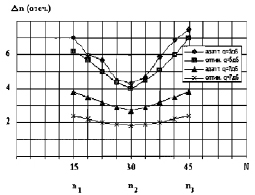
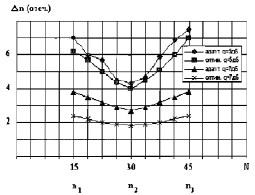
Рис. 5.9. Зависимость ошибок оценки координат точек контура от размеров фрагмента (а) и расположения точек (б)
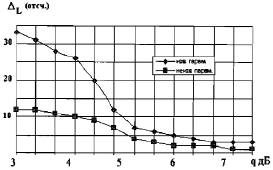
Рис. 5.10. Ошибка оценки протяженности РЛИ цели в одном канале от величины среднего радиолокационного контраста при известных и неизвестных параметрах σ1 σ2
Цель идентификации заключается в отыскании оптимальной в рамках выбранного критерия оценки совокупности векторов 
, у которых каждая компонента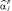 
представляет собой оценку истинного номера j-й цели в р-м обзоре. На уже упоминавшемся примере (рис. 5.8) условно показаны карты анализируемой поверхности в трех последовательных обзорах. На каждой из этих карт расположены три РЛИ ПРЦ, которые условно изображены в виде треугольника, квадрата и круга. При простейшей идентификации целей (например, по минимуму изменения расстояния от отметки в предыдущем обзоре) второй и третий ПРЦ во втором обзоре будут перепутаны (они поменялись местами за счет перемещения по неизвестным для наблюдателя траекториям, изменения ракурса, траектории ИСЗ и т.п.). Правильное же решение должно иметь вид:
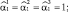
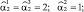
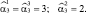
Общее число возможных гипотез об истинном расположении ПРЦ в пределах анализируемых карт акватории, полученных при Р обзорах, равно Р·М!. Если для каждой из гипотез может быть записана ее апостериорная плотность вероятности, то решения следует принимать по ее максимуму:
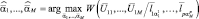(5.5.2)
В тех случаях, когда векторы параметров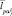 
априори неизвестны, их значения в должны быть заменены соответствующими оценками максимального правдоподобия, полученными в предположении о справедливости проверяемой гипотезы.
Проиллюстрируем решение названной задачи на примере флуктуационных РЛИ ПРЦ, причем при идентификации отсутствует какая-либо априорная информация за исключением того факта, что отсчеты РЛИ независимы и распределены по экспоненциальному закону, что соответствует выборочным отсчетам мощности. В этом случае параметры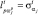 
представляют собой дисперсии соответствующих отсчетов. Алгоритм принимает вид:
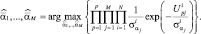(5.5.3)
Поскольку значения мощностей отдельных отсчетов априори неизвестны и при решении задачи идентификации отсутствует возможность их определения откуда-либо, кроме как из наблюдаемой совокупности РЛИ различных ПРЦ, воспользуемся максимально правдоподобными оценками неизвестных мощностей:
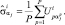(5.5.4)
После подстановки (5.5.4) в (5.5.3) и (5.5.2) и логарифмирования получаем алгоритм идентификации РЛИ ПРЦ при межобзорном наблюдении:
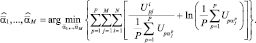(5.5.5)
Для анализа эффективности предлагаемого правила рассмотрен пример идентификации двух РЛИ ПРЦ (М = 2), которые моделировались в 4 (Р = 4) последовательных обзорах. РЛИ ПРЦ не отличались по величине удельной ЭПР, но отличались размерами (при общем размере радиолокационной карты 100×100 элементов разрешения площадь первого РЛИ – 5×5, а второго – 4×4 элементов разрешения). Положение центра РЛИ ПРЦ на карте в каждом обзоре моделировалось равновероятным при условии, что контуры РЛИ не пересекаются.
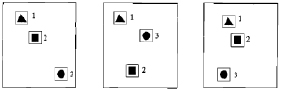
Рис. 5.11. Карты поверхности с РЛИ трех разных ПРЦ
Таким образом, в каждом отдельном испытании были реализованы восемь конкурирующих гипотез о порядке последовательного размещения РЛИ на карте акватории.
Зависимости вероятностей ошибок от отношения сигнал/фон приведены на рис. 5.12, откуда, в частности, следует, что две цели с одинаковыми ЭПР (наихудший для практики случай) и отличающиеся по линейным размерам приблизительно на 25 % идентифицируются с вероятностью ошибки не более 0,1 при отношении сигнал/фон порядка 20 дБ.
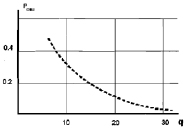
Рис. 5.12. Вероятность ошибки идентификации