Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОПТИМАЛЬНАЯ ОБРАБОТКА РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ, ФОРМИРУЕМЫХ В РСА

Доросинский Л. Г.,

5.7.1. Разработка алгоритма

В работах [15, 16], посвящённых проблемам обработки сигналов в радиолокационной станции с синтезированной апертурой (РСА), основное внимание уделялось исследованию алгоритмов обнаружения при действии помех, вызванных отражениями от подстилающей поверхности и шумом. В ряде практических ситуаций вместе с полезным сигналом, отраженным от многоэлементной цели, в диаграмме направленности (ДН) РСА могут присутствовать достаточно мощные помеховые сигналы, вызванные отражениями от мешающих объектов. В этих случаях алгоритм обработки должен строиться с учётом, как распределённого характера цели, так и наличия помех. Определение основных принципов построения таких алгоритмов и методов их анализа составляет содержание данной работы.

Предположим, что РСА бокового обзора перемещается по прямолинейной траектории. Полезные и мешающие сигналы в одном элементе разрешения по дальности формируются отдельными отражателями, отстоящими на расстояни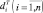и и 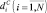от начала координат с шагом Δd, причём n и N – числа сигнальных и помеховых отражателей соответственно (рис. 5.15). При дискретной во времени обработке вектор наблюдаемых данных может быть представлен в следующем виде:

Y = β_TA_T + β_СA_С + N_N, (5.7.1)

где β_T – матрица M×n:

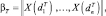(5.7.2)

состоящая из векторов

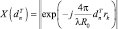(5.7.3)

задающих фазовое распределение сигнала, отражённого от i-го элемента цели, по точкам синтезированной апертуры, имеющим координаты r_k, 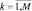, (λ – длина волны); A_T и A_С – векторы комплексных амплитуд сигналов и помех размерностью n×1 и N×1 соответственно, представляющие собой нормальные случайные величины с нулевыми математическими ожиданиями и дисперсиям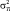и и 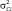соответственно; матрица β_С определяется аналогично (2) и (3), N_N – вектор комплексных амплитуд гауссовского шума.

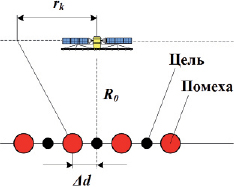
Рис. 5.15. Геометрия задачи

При записи наблюдаемых данных в виде (5.7.1) достаточной статистикой для обнаружения полезного сигнала является квадратичная форма

α = Y*^TθY, (5.7.4)

где 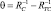– весовая функция обработки,

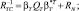(5.7.5)

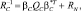(5.7.6)

где R_TC и R_C – корреляционные матрицы вектора (5.7.1) при наличии и отсутствии полезного сигнала соответственно,

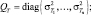(5.7.7)

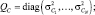(5.7.8)

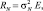(5.7.9)

где * – комплексное сопряжение; T – знак транспонирования; E – единичная матрица, без ограничения общности в дальнейшем считаем дисперсию шума .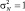

Используя равенство Вудбери для определения оптимальной весовой функции, запишем выражение достаточной статистики в виде

α = Z^*T PZ, (5.7.10)

где 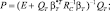(5.7.11)

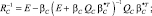(5.7.12)

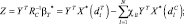(5.7.13)

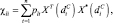(5.7.14)

где p_lt – элемент матрицы (5.7.11).

Структурная схема, реализующая оптимальный алгоритм (5.7.10), показана на рис. 5.16.

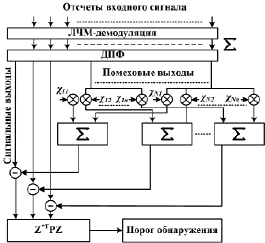
Рис. 5.16. Структурная схема оптимального алгоритма

Основная функциональная операция, входящая в (5.7.13):

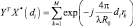(5.7.15)

представляет собой ЛЧМ-демодуляцию и дискретное преобразование Фурье, вычисляемое для пространственных частот 2d_i/λR₀, соответствующих всем элементам цели (помех).