
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.2. Объем реакционной системы в процессе термоокислительной деструкции
Авторы [6] предложили использовать для сравнительной оценки термостабильности полимерных материалов константу k* (эффективную константу скорости окисления). Параметр k* служит для характеристики скорости поглощения кислорода образцом полимерного материала и для высокотемпературного окисления дается так [6]:
![]() , (8.9)
, (8.9)
где ![]() - количество поглощенного кислорода; t- время;
- количество поглощенного кислорода; t- время; ![]() - давление кислорода над полимером.
- давление кислорода над полимером.
После определенных преобразований была получена формула для описания зависимости ![]() следующего вида [6]:
следующего вида [6]:
![]() , (8.10)
, (8.10)
где ![]() - начальное давление кислорода над полимером; V - объем реакционной системы; m - масса полимера; R - универсальная газовая постоянная; Тст - температура теплового старения.
- начальное давление кислорода над полимером; V - объем реакционной системы; m - масса полимера; R - универсальная газовая постоянная; Тст - температура теплового старения.
Отметим, что в уравнении (8.10) существует физическая неопределенность параметров V и m. В качестве этих параметров нельзя принять объем и массу полимерного образца, поскольку, как отмечалось выше, во время эксперимента часть мономерных звеньев ведет себя как инертное вещество [6].
Исходя из этого, авторы работы [27] выполнили исследование физического смысла объема реакционной системы на примере ПАр и ПААСО, полученных разными способами поликонденсации (см. табл. 6.1).
Поскольку для расплавов исследуемых полимеров основным структурным элементом является макромолекулярный клубок, то в качестве объема реакционной системы авторы [27] приняли объем клубка Vкл. Величина Vкл может быть рассчитана следующим образом [28]:
![]() , (8.11)
, (8.11)
где Rg - радиус инерции клубка; h - линейный масштаб измерения. Для простоты в дальнейшем для всех исследуемых полимеров в работе [27] были приняты одинаковые значения Rg = 10 и h = 5 относительных единиц.

Однако, непосредственное использование Vкл в уравнении (8.10) не дает корректных результатов. Это объясняется тем, что в рассматриваемом случае исследуются процессы термоокислительной деструкции фрактальных объектов (макромолекулярных клубков), т.е., указанные процессы протекают не в евклидовом, а во фрактальном пространстве. Как указано выше, это означает, то кислород поглощается в части макромолекулярного клубка, подвергающейся деструкции. Тогда эффективный объем клубка ![]() , поглощающий кислород, можно определить так [27]:
, поглощающий кислород, можно определить так [27]:
![]() . (8.12)
. (8.12)
Далее уравнение (8.10) можно переписать в следующем упрощенном виде [27]:
![]() , (8.13)
, (8.13)
где c7 - константа.
На рис. 8.7 приведено сравнение экспериментальных и рассчитанных согласно уравнению (8.13) зависимостей ![]() для ПАр-3, ПААСО-1 и ПААСО-2 при температуре теплового старения Тст = 623 К. Как можно видеть, для указанных полимеров получено хорошее соответствие теории и эксперимента. Аналогичный результат получен и для остальных ПАр и ПААСО при разных температурах теплового старения. Характерно, что величина c7 не зависит от способа поликонденсации и, следовательно, от структуры полимерного расплава и равна ~ 0,260 для ПАр и ~ 0,152 для ПААСО. Это обстоятельство позволяет оценить величину k*. Сравнение уравнений (8.10) и (8.13) показывает, что k*mR = 1. Далее, исходя из этого условия, использованием уравнения (8.10) можно получить [27]:
для ПАр-3, ПААСО-1 и ПААСО-2 при температуре теплового старения Тст = 623 К. Как можно видеть, для указанных полимеров получено хорошее соответствие теории и эксперимента. Аналогичный результат получен и для остальных ПАр и ПААСО при разных температурах теплового старения. Характерно, что величина c7 не зависит от способа поликонденсации и, следовательно, от структуры полимерного расплава и равна ~ 0,260 для ПАр и ~ 0,152 для ПААСО. Это обстоятельство позволяет оценить величину k*. Сравнение уравнений (8.10) и (8.13) показывает, что k*mR = 1. Далее, исходя из этого условия, использованием уравнения (8.10) можно получить [27]:
![]() . (8.14)
. (8.14)
Поскольку в эксперименте работы [27] величина ![]() была постоянной и равной 0,1 МПа, то из уравнения (8.14) следует равенство k* и с7 с точностью до константы. Из уравнения (8.10) нетрудно видеть, что увеличение k* или с7 приводит к росту
была постоянной и равной 0,1 МПа, то из уравнения (8.14) следует равенство k* и с7 с точностью до константы. Из уравнения (8.10) нетрудно видеть, что увеличение k* или с7 приводит к росту ![]() и, следовательно, снижению устойчивости полимера к термоокислительной деструкции. Из приведенных выше значений с7 следует, что в этом смысле ПААСО предпочтительнее ПАр [27].
и, следовательно, снижению устойчивости полимера к термоокислительной деструкции. Из приведенных выше значений с7 следует, что в этом смысле ПААСО предпочтительнее ПАр [27].
Как было показано в работе [6], между параметром k* и обычной константой скорости термоокислительной деструкции kd (см. табл. 6.1) существует следующая взаимосвязь:
k* = gpkd, (8.15)
где gр - коэффициент растворимости кислорода.
На рис. 8.8 приведена зависимость величины gр, определенной согласно уравнению (8.15), в относительных единицах от фрактальной размерности макромолекулярного клубка Df. Эта зависимость объясняет условие k* = const для каждого из рассмотренных полимеров: увеличение Df повышает gр и одновременно снижает kd (см. уравнение (1.49)).
На первый взгляд представляется, что повышение Df или увеличение степени компактности макромолекулярного клубка должно снижать, а не увеличивать растворимость кислорода gр. Однако, этот эффект легко объясняется в рамках фрактальной модели растворимости газов в полимерах [29] (см. главу 2). Как следует из уравнения (2.18), увеличение размерности Df при неизменных эффективной площади поперечного сечения молекулы растворяющегося газа Sм и характеристической силовой постоянной потенциала Леннарда-Джонса для взаимодействий газ-газ (e/k)эф (поскольку речь идет об одном и том же газе - кислороде) должно привести к росту gр. В свою очередь, увеличение Df при повышении Df следует из уравнения (1.47).

Таким образом, изложенные выше результаты показали, что объемом реакционной системы в случае термоокислительной деструкции полимерного расплава является только часть макромолекулярного клубка, определяемая его фрактальной размерностью в рамках теории дробных производных. Такая зависимость возможна только для фрактальных объектов, а для евклидовых объектов объем реакционной системы равен нулю. Иначе говоря, термоокислительная деструкция полимеров возможна только в случае фрактальности их структуры [27].
Рассмотрим другие аспекты применения понятия «объем реакционной системы». В работе [20] было показано, что увеличение Nст приводит к существенному росту исходного содержания кислорода ![]() в образцах - от ~ 2,50 до 13,8 моль О2/осн. моль полимера в интервале Тст = 573 ¸ 723К. Этот эффект естественно связать с изменением объема макромолекулярного клубка Vкл как функции Тст. Существует ряд методов расчета объема фрактальных объектов, один из которых представлен уравнением (8.11). Авторы [30] использовали другое соотношение, полученное в работе [31], а именно, уравнение (2.61). Гамма-функция Эйлера Г(Df./(2 + 1)) может быть рассчитана следующим образом [31]:
в образцах - от ~ 2,50 до 13,8 моль О2/осн. моль полимера в интервале Тст = 573 ¸ 723К. Этот эффект естественно связать с изменением объема макромолекулярного клубка Vкл как функции Тст. Существует ряд методов расчета объема фрактальных объектов, один из которых представлен уравнением (8.11). Авторы [30] использовали другое соотношение, полученное в работе [31], а именно, уравнение (2.61). Гамма-функция Эйлера Г(Df./(2 + 1)) может быть рассчитана следующим образом [31]:
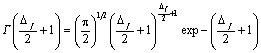 . (8.16)
. (8.16)
Как и ранее, величина Rg в уравнении (2.61) принята равной 10 относительных единиц и одинаковой для всех рассмотренных ПАр и ПААСО.
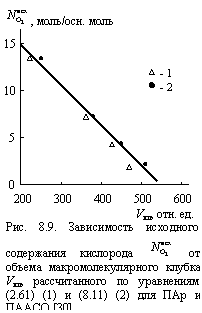
На рис. 8.10 приведена зависимость ![]() для ПАр и ПААСО с использованием обоих рассмотренных выше способов расчета Vкл. Как можно видеть, получено ожидаемое увеличение
для ПАр и ПААСО с использованием обоих рассмотренных выше способов расчета Vкл. Как можно видеть, получено ожидаемое увеличение ![]() по мере роста
по мере роста ![]() , причем эта корреляция линейна и проходит через начало координат [32].
, причем эта корреляция линейна и проходит через начало координат [32].
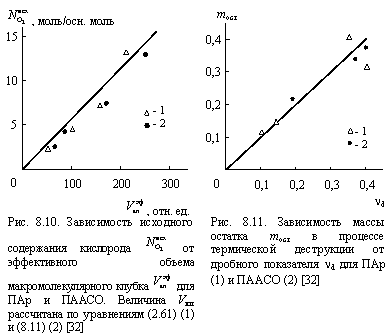
Далее можно предположить, что остаток массы полимера mост, сохранившийся в процессе термической деструкции, будет равен (или пропорционален) nd. Действительно, приведенная на рис. 8.11 зависимость mост(nd) линейна и проходит через начало координат. Из этой зависимости следует приблизительное тождество mост »nd [32].
Таким образом, основой применения теории дробных производных для описания термоокислительной деструкции полимерных расплавов является неоднородность их структуры, допускающая реализацию деструкции только в части макромолекулярного клубка [30; 32].
