Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

8.3. Описание кинетики окисления в рамках уравнения Миттаг-Лефлера

Как отмечалось выше, существует несколько основных типов кинетических кривых «количество поглощенного кислорода - время»  в процессе термоокислительной деструкции полимеров. Один из таких типов, а именно, кривые с автозамедлением, будет рассмотрен в настоящем разделе [33]. В рамках классической химической трактовки замедление поглощения кислорода со временем объясняется «выгоранием» реационноспособных групп [5].

Однако, возможна и другая теоретическая трактовка кинетических кривых   указанного типа, основанная на концепции фрактала. В связи с этим следует сделать два замечания. Во-первых, кривые указанного типа, где наблюдается снижение скорости процесса со временем его протекания, широко распространены в физике и химии полимеров и не только полимеров. К таковым следует отнести кривые сорбции [2], аннигиляции позитронов [12], кинетические кривые «степень завершенности (конверсии) реакции - время» при синтезе полимеров [34], кривые «напряжение - деформация» [35] и т.д. Во-вторых, уже сам факт зависимости скорости процесса от времени предполагает фрактальность среды, в которой этот процесс протекает [36]. Это дает возможность предположить, что причины замедления поглощения кислорода со временем для кинетических кривых  автозамедленного типа носят гораздо более общий характер, чем предполагалось ранее [5; 6]. Как отмечалось выше, такой причиной может быть фрактальность среды, в которой протекает термоокислительная деструкция.

Можно указать два возможных фрактальных подхода к описанию кривых   автозамедленного типа. Первый из них связан с использованием представлений геометрии фрактальной (Хаусдорфовой) размерности. Такой подход успешно использован в главах 6 и 7 для описания кривых   указанного типа. Второй из указанных подходов связан с использованием математического аппарата дробного интегро-дифференцирования [1; 2; 12; 37; 38]. Примеры успешного применения этого подхода для описания термоокислительной деструкции полимерных расплавов можно найти в настоящей главе.

Для теоретического описания кинетики окисления автозамедленного типа в рамках теории дробных производных авторы [33] использовали следующее уравнение [12]:

,                         (8.17)

где  - исходное содержание, кислорода,  - функция Миттаг-Лефлера, которая имеет вид [39]:

, n_d > 0, t > 0,      (8.18)

где n_d - дробный показатель; Г - гамма-функция Эйлера, а величина k = 1, 2, 3 (что достаточно для получения в практических приложениях точности [39]). Гамма-функция Эйлера определена следующим образом в общем виде для переменной х (частный случай для х = (D_f/2+1) дан уравнением (8.16)) [31]:

.                                         (8.19)

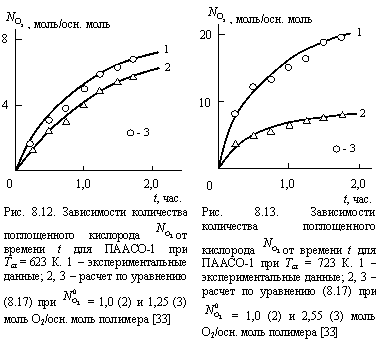
Дробный показатель n_d определяется согласно уравнению (6.1) и характеризует долю фрактала (макромолекулярного клубка), сохраняющуюся в процессе эволюции (деструкции). В случае n_d = 1 уравнение для описания кривых  автозамедленного типа записывается следующим образом [2]:

,                                  (8.20)

где N - некоторая константа.

В рамках классического подхода кинетика автозамедленного типа описывается уравнением (8.1). Из уравнения (6.1) следует, что n_d = 1 соответствует D_f = d, т.е., протеканию реакции окисления в евклидовом (а не фрактальном) пространстве и сравнение уравнений (8.1) и (8.20) показывает, что классическое уравнение (8.1) является частным (предельным случаем более общего уравнения (8.20) для описания реакции окисления в евклидовых средах. При этом характерно использование в уравнении (8.1) экспоненциальной функции, которая широко применяется в традиционной физике и указывает на протекание процессов именно в евклидовых средах. Функция Миттаг-Лефлера играет аналогичную роль для фрактальных сред.

На рис. 8.12 и 8.13 приведены экспериментальные (кривые 1) и рассчитанные согласно уравнению (8.17) при = 1,0 (кривые 2) зависимости  для ПААСО-1 при температурах теплового старения 623 и 723 К, соответственно. Как можно видеть, между теоретическими и экспериментальными кривыми   наблюдается полная симбатность, а получить их количественное соответствие можно, определив константу   в уравнении (8.17) методом наилучшего соответствия. Так, для кривой   на рис. 8.12  » 1,25 моль О₂/осн. моль полимера, а для кривой   на рис. 8.13  » 2,55 моль О₂/моль осн. полимера. Поскольку величина   представляет собой исходное содержание кислорода в макромолекулярных клубках расплава, то следует ожидать корреляции между этим параметром и структурой макромолекулярного клубка, причем ожидается следующий характер такой корреляции: уменьшение плотности макромолекулярного клубка или снижение D_f должно привести к росту . Показанная на рис. 8.14 зависимость (D_f) подтверждает это предположение. Как и следовало ожидать, при D_f = d = 3 (плотный или евклидов объект) величина   экстраполируется к нулевому значению, т.е., согласно уравнению (8.17) окисление для евклидовых объектов невозможно и реакции термоокислительной деструкции могут протекать только во фрактальных средах [33]. Следовательно, изложенные в настоящем разделе результаты показали, что фрактальный подход с использованием математического аппарата дробного дифференцирования дает адекватное описание кинетических кривых поглощения кислорода при окислении полимеров автозамедленного типа. При этом получена ясная физическая интерпретация дробного показателя как части макромолекулярного клубка, не подвергающейся окислению в процессе термоокислительной деструкции полимерного расплава. Используемое для этой же цели классическое уравнение является частным (предельным) случаем фрактального соотношения применительно к евклидовым средам. Константа в базовом фрактальном соотношении представлена как исходное содержание кислорода, которое также является функцией структуры макромолекулярного клубка [33].