Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

АВТОМАТИЗАЦИЯ МЕДИЦИНСКОЙ ЭКСПЕРТИЗЫ НАЗНАЧЕНИЯ ЛЬГОТНЫХ ЛЕКАРСТВ

Кошкаров А. А., Рубцова И. Т., Семенов А. Б., Халафян А. А.,

2.3.2. Определение рейтинга муниципальных образований по обеспечению лекарственными препаратами

Вместе с тем, количество выявленных нарушений в медицинских организациях при выписке льготных рецептов может служить показателем эффективности обеспечения необходимыми лекарственными препаратами отдельных категорий граждан. Поэтому особую актуальность приобретает проблема определения рейтинга муниципальных образований (районов) края по совокупности всех рассмотренных 17 критериев МЭК.

Для оценки эффективности деятельности по ОНЛП муниципальных образований использован метрический подход, основанный на методе иерархической классификации, который предполагает вычисление расстояний между районами как точками многомерного пространства в системе координат, соответствующей критериям их эффективности. Введено понятие эталонного района, который аккумулирует наилучшие значения критериев всех муниципальных образований. Рейтинги районов устанавливаются в соответствии с расстояниями до эталонного муниципального образования – чем меньше расстояние, тем эффективнее район и выше его рейтинг (место в списке районов). Метод реализован в среде статистического пакета STATISTICA.

Существующие методы ранжирования объектов по совокупности количественных показателей, как правило, сводятся либо к построению интегрального критерия в виде аддитивной, или мультипликативной функции показателей с весовыми коэффициентами, отражающими их относительный вклад в критерий, либо к переводу всех критериев в балльную шкалу с последующим суммированием баллов [141]. К последнему методу можно отнести определение рейтингов (рангов) объектов по каждому критерию с дальнейшим суммированием рангов. Наивысший рейтинг будет у объекта с минимальной суммой рангов. Указанные методы обладают определенными недостатками, делающими сомнительным их использование. Например, не формализована процедура выбора весовых коэффициентов – их
назначение опирается на мнение, опыт лица принимающего решение, либо экспертов. Но сколько экспертов, столько и мнений, причем могут быть и диаметрально противоположные, иногда такой способ выбора весов называют «потолочным». Недостаток метода еще и в том, что незначительное изменение весов как правило, приводит к существенному изменению значения интегрального критерия, а значит и рейтингов. Перевод количественных показателей в балльную шкалу, или определение рейтинга по каждому показателю с последующим суммированием баллов, также имеет значительные недостатки, так как:

– балльная (порядковая) шкала «бедная» и переход к ней сопровождается существенной потерей информации об объекте;

– в порядковой шкале в принципе не определена операция суммирования, так как баллы (ранги) указывают лишь степень предпочтения одного объекта перед другим, выраженным в символической числовой форме.

Не выдерживают критики и предлагаемые многочисленные способы перевода количественных показателей в балльную шкалу, например, как это сделано в [35], что приближает их по математической обоснованности к «потолочным» методам. Сказанное относится и к широко распространенным в медицине балльным шкалам apache, позволяющим оценивать тяжесть состояния больных.

Применение балльных шкал в медицине и здравоохранении было оправдано при отсутствии возможности эффективного использования многомерных методов классификационного анализа. Сейчас в эпоху всеобщей компьютеризации и появления самого широкого спектра статистических пакетов открылись совершенно новые горизонты применимости пакетных методов обработки медицинских данных [134]. Здесь уместным является риторический вопрос: «Зачем сбивать яблоки палками, если можно приставить лестницу?». Такой «лестницей» при анализе эмпирических данных любой природы, в том числе и в медицине и здравоохранении являются многомерные методы анализа данных, реализованные в статистических пакетах. Балльной шкалой разумно пользоваться только в том случае, если отсутствует возможность измерения показателей, характеризующие объекты исследования в количественных шкалах – отношений, интервальной и абсолютной. Как правило, в этих случаях прибегают к экспертным оценкам в порядковой, балльной шкале.

Предположим, что заданы m объектов О1, О2, …, Оm и совокупность n показателей Q1, Q2, …, Qn, которые определяют их качественные характеристики (критерии). Значение j-го критерия, которое соответствует i-му объекту обозначим как qij, 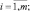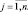Если объект Оk предпочтительнее объекта Оl (Оk  Оl), то qkj > (или <) qlj, где «» знак предпочтения. Будем использовать знак «>», если предпочтению соответствует большее значение критерия, знак «<» в обратном случае. Составление рейтинга по сути эквивалентно ранжированию объектов по степени предпочтения относительно всех критериев Qj,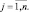

Одним из наиболее известных подходов к решению этой многокритериальной задачи является сведение к однокритериальной, когда вводят так называемый интегральный критерий Qs, представляющий собой скалярную функцию от критерия Qj, 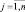[92]:

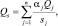(2.1)

где aj – вес, отражающий относительный вклад частного критерия Qj в интегральный критерий; sj – коэффициент, который позволяет перейти к безразмерным величинам от Qj. И так как критериям должны соответствовать различные характеры предпочтения, если предпочтению соответствует максимальное значение критерия, весу aj присваиваиваем знак (+), и знак (–) в противном случае.

Но данный способ обладает существенным недостатком, так как не формализована процедура выбора весовых коэффициентов. Интегральный критерий Qs очень чувствителен к изменению весов, поэтому велика вероятность получения ошибочного решения задачи. Методы Саати и Коггера и Ю К можно отнести к данному подходу, поскольку предполагают нахождение весовых коэффициентов [137].

Составление рейтинга объектов (их ранжирование) предполагает их сравнение. Рассмотрим метрический подход, когда известны числовые значения критериев, которые характеризуют качество объектов и основанный на их представлении как точек n-мерного пространства и определении сходства (различия) между ними через расстояние метрических пространств.

Значения qij, 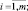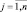можно представить как таблицу (матрицу) с числом строк и столбцов, равными соответственно количеству объектов m и количеству столбцов n:

(2.2)

Строки таблицы соответствуют объектам Oi, столбцы – критериям Qj. Представленная матричная запись объектов позволяет рассматривать их как точки n-мерного пространства в системе координат Q1, Q2, …, Qn, с координатами qi1, qi2, …, qin и оценивать расстояние между ними при помощи одной из метрик, которые реализованы в модуле Кластерный анализ пакета STATISTICA [135], например посредством евклидова расстояния:

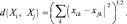(2.3)

Для ранжирования объектов рассмотрен гипотетически эталонный объект 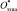, который аккумулирует наилучшие свойства всех объектов. Тогда, координатами 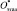будут значения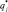 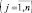, доставляющие наибольшее или наименьшее значение критериев, в зависимости от характера предпочтения:

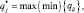
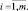(2.4)

По расстояниям между объектами О1, О2, …, Om, и эталоном 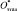, вычисленным по формуле (2.3) легко их ранжировать по принципу – чем меньше расстояние, тем выше рейтинг и меньше номер (ранг) объекта в списке.

На значения расстояний могут сильно влиять различия между единицами измерения осей (критериев), поэтому целесообразно столбцы матрицы (2.2) предварительно привести к безразмерному виду нормированием.

Если нормированные значения обозначить через 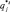, , 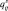а расстояние между объектами Оi и эталоном  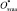– di, то:

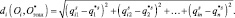(2.5)

Для составления рейтинга достаточно объекты расположить в порядке возрастания di. Номера объектов в списке 1, 2, …, m будут их рангами. Объект с рангом 1 будет наилучшим, так как ему соответствует минимальное расстояние к эталону, объект с рангом m будет худшим, так как ему соответствует наибольшее расстояние.

C помощью предложенного нами метрического подхода [137; 141–143] были определены рейтинги 45 районов Краснодарского края по количеству выявленных нарушений ОНЛП в медицинских организациях за год по 17 критериям МЭК (табл. 2.6).

Таблица 2.6

Количество нарушений при ОНЛП на 1000 рецептов за год

Продолжение табл. 2.6 (справа)

Продолжение табл. 2.6 (справа)

Окончание табл. 2.6 (справа)

Примечание. * Критерии, которые принимают значение 0 у всех районов, не использовались для построения рейтинга.

Используя метод иерархической классификации, реализованный в программе STATISTICA по стандартизованным значениям показателей были вычислены расстояния между районами. В столбце Расстояние до эталона представлены расстояния между всеми 45 муниципальными образованиями и Эталоном. При этом, чем эффективнее организация, тем меньше расстояние, районы в таблице упорядочены по их возрастанию. В столбце Рейтинг отображены места (рейтинги) районов в соответствии с их порядком в таблице. Самый высокий рейтинг – первое место у Новокубанского района, далее идут Тимашевский район – второе место, Крымск – третье место, Кущевский район – четвертое место и т.д.

Как видно из таблицы по рейтингам можно установить только порядок, или место в списке, но невозможно оценить степень близости (сходства) районов друг к другу. Для получения интегрального количественного показателя, более полно характеризующего эффективность районов, воспользуемся данными столбца Расстояние до эталона. Эталонный район нам был нужен для определения рейтинга муниципальных образований, который позволил определить лидера районов по совокупности рассмотренных 17 показателей. Для получения интегральной оценки эффективности районов в качестве точки отсчета будем считать лидера муниципальных образований – Новокубанский район. Коэффициент kэф, или интегральный критерий эффективности районов определим как долю (процент) который составляет расстояние лидера до эталонного объекта от расстояний районов до эталонного объекта, т.е.

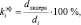i = 1, …, 45.

Естественно, при таком определении коэффициент эффективности лидера – Новокубанского района составит 100 %. Коэффициенты эффективности районов отображены в столбце . Еще раз подчеркнем, что при таком подходе эффективность райноы оценена относительно муниципального образования лидера.

Используя метод иерархической классификации, реализованный в программе STATISTICA, сделан анализ сходства и различия районов посредством кластерной структуры, изображенной в виде дендрограммы на рис. 2.9.

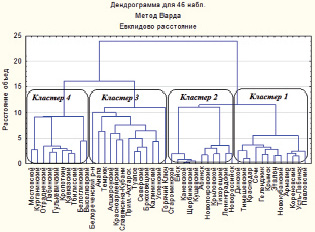
Рис. 2.9. Дендрограмма кластерной структуры районов

Вдоль горизонтальной оси указаны названия районов, вдоль вертикальной оси – расстояние между ними, которое является критерием объединения в кластеры. При расстоянии равном 0, каждый район образует самостоятельный кластер – группу однородности, состоящую из одного объекта. По мере увеличения расстояния новые районы объединяются в группы, т.е. постепенно понижается порог, относящийся к решению об объединении двух или более объектов в один кластер. Как итог связывается всё большее число районов в группы, которые агрегируются в более крупные кластеры, состоящие из все более различающихся муниципальных образований. На последнем шаге все районы окончательно объединяются в один кластер – исходную совокупность из 45 муниципальных образований.

Следует учитывать, что из принадлежности объектов к группам однородности не следует их соседство в рейтинговом списке. Так, лидер рейтинга, Новкубанский район входит в состав Кластера 1. Но наиболее близкие к нему муниципальные образования Крымск,
Геленджик и Сочи занимают 3, 8 и 12 места соответственно. Выявленная закономерность не является противоречием и, легко объяснима структурой многомерного пространства. Обратимся к методу многомерного шкалирования, который позволяет перенести объекты многомерного пространства, в нашем случае – размерности 12 в пространство меньшей размерности, например 2 На рис. 2.10 отображена диаграмма рассеяния в новой системе координат – Измерение 1, Измерение 2.

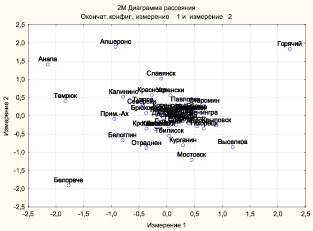
Рис. 2.10. Диаграмма рассеяния районов

Эталон внутри муниципальных образований, но видны периферийные – Анапа (последнее место в рейтинге), Темрюк (43) и так далее. На рис. 2.11 отображена диаграмма рассеяния первых 10 районов по рейтингу.

Из диаграммы видно, что наиболее близко расположены Щербиновский и Каневской районы. Если вернуться к рис. 2.9, то видно, что изначально они образуют кластер, далее к ним присоединяется Кущевский район. При этом ближе всех к Эталону расположен Новокубанский район, что соответствует его первому месту в рейтинге.

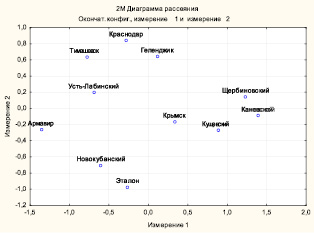
Рис. 2.11. Диаграмма рассеяния первых 10 районов

Таким образом, предложенный метрический подход позволил построить рейтинг муниципальных образований Краснодарского края по количеству выявленных нарушений ОНЛП в принадлежащих к ним по территориальному принципу медицинских организациях, вычислить значения коэффициента эффективности, исследовать их кластерную структуру.