Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Структурная стабилизация полимеров: фрактальные модели

Долбин И. В., Козлов Г. В., Заиков Г. Е.,

8.4. Методы прогнозирования кинетических кривых и конечных параметров окисления полимеров

Как отмечалось выше, эффективная константа скорости окисления k_d в уравнении (8.1) по своему физическому смыслу является подгоночным коэффициентом, определяемым из соотношения между скоростью реакции W и концентрацией реагирующих веществ [A] и [B] [6]:

W = k_d[A]^p[B]_q,                                                    (8.21)

где р и q - порядок реакции по реагентам [A] и [B], соответственно.

Хотя и подчеркивается [5], что величина k_d зависит от структуры полимеров, но конкретной формы такой зависимости в настоящее время не установлено. Развитие в последние годы методов фрактального анализа [20; 40; 41] дает инструмент для получения количественной взаимосвязи параметров уравнения (8.1)  и k_d со структурой полимеров. В работах [42; 43] эти вопросы рассмотрены на примере расплавов ПАр и ПААСО, полученных разными способами поликонденсации (см. табл. 6.1).

На рис. 8.15 приведены кинетические кривые   для ПАр при одной и той же температуре теплового старения 723 К. Как можно видеть, поглощение кислорода зависит от метода поликонденсации, которым получен полимер, или от его структуры.

Оценки параметра   согласно уравнению (8.1) показали значительную (до 3 раз) вариацию его величины для полученных разными способами поликонденсации полимеров даже при одной и той же температуре теплового старения. Это означает, что предельное количество поглощаемого кислорода в уравнении (8.1) по существу является подгоночным параметром. В то же время оценки показали [44], что для окисления всех метильных и алифатических групп ПААСО требуется   » 24,1 моль О₂/осн. моль полимера. Кроме того, из данных рис. 8.15 следует, что при некотором значении   кинетические кривые   достигают своего асимптотического значения  , т.е., выходят на плато. Величина   зависит от температуры теплового старения и способа поликонденсации, т.е., от структуры полимера, характеризуемой размерностью D_f. Особенно четко выход кривых   на участок плато прослеживается для высоких температур теплового старения, где процессы термоокислительной деструкции протекают достаточно быстро (см. рис. 8.15). В рамках классического подхода выход кинетических кривых на участок плато объясняется «выгоранием» реакционноспособных групп. Кроме того, уравнение (8.1) предполагает, что условие  =   достигается только при t ® ¥.

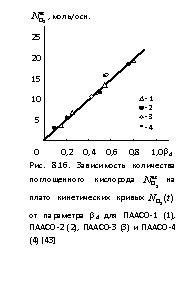
Как показано выше, в рамках теории дробных производных величина   оценивается согласно уравнению (8.2). Далее можно построить зависимость   от величины b_d, т.е., доли макромолекулярного клубка, подвергающейся деструкции. Такая зависимость приведена на рис. 8.16 и из нее следует линейная корреляция между   и b_d, по наклону которой можно определить коэффициент пропорциональности, равный ~ 24,4 моль О₂/осн. моль полимера. Эта величина превосходно согласуется с оценкой предельного количества поглощенного кислорода  , рассчитанного по химическому строению ПААСО. Следовательно, выход кинетических кривых  на плато означает деструкцию доступной для этого процесса части макромолекулярного клубка, характеризуемой параметром b_d. Далее этот процесс замедляется и может завершиться полным разрушением макромолекулярного клубка только при t ® ¥ (уравнение (8.1)) [42].

Изложенные выше соображения предполагают, что увеличение b_d должно привести к повышению скорости термоокислительной деструкции и, как следствие, к росту k_d. По аналогии с уравнением (8.1) для кинетических кривых   автозамедленного типа можно записать [43]:

 

,                                                (8.22)

где с₈ - константа.

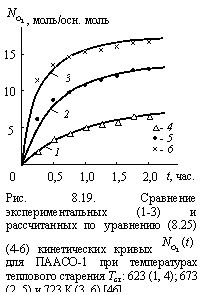
Уравнение (8.22) довольно успешно (при с₈ = 0,5 ´ 10^-4) описывает экспериментальные кривые , что подтверждается данными рис. 8.17. Тем не менее, нет оснований рекомендовать его для этих целей, как минимум, по двум причинам. Во-первых, в этом уравнении вновь появляется эмпирический подгоночный коэффициент с₈. Во-вторых, как следует из данных рис. 8.17, наблюдается некоторое качественное несоответствие экспериментальных и теоретических кривых  . Причина этого несоответствия очевидна: как показано выше, для описания процессов во фрактальных пространствах следует использовать функцию Миттаг-Лефлера, а не экспоненциальную функцию, строго корректную только для евклидовых пространств [2]. Тем не менее, уравнение (8.22) полезно стой точки зрения, что сравнение показателей экспонент этого уравнения и соотношения (8.1) позволяет получить следующую аппроксимацию [43]:

k_d » 0,5 ´ 10^-4 b_d.                                               (8.23)

На рис. 8.18 приведено соотношение между k_d и 0,5 ´ 10^-4 b_d, которое хорошо аппроксимируется линейной корреляцией с единичным наклоном, проходящей через начало координат. Это обстоятельство позволяет утверждать, что величина k_d является функцией структуры макромолекулярного клубка. При b_d = 0 (или D_f = d = 3, см. уравнение (6.3)) термоокислительная деструкция прекращается (k_d = 0). Это положение подтверждается хорошо известным на практике случаем: термоокислительная деструкция не реализуется в кристаллических областях аморфно-кристаллических полимеров, поскольку указанные области являются трехмерно упорядоченным евклидовым объектом [6].

Таким образом, методы фрактального анализа и дробного дифференцирования позволяют получить количественные соотношения параметров термоокислительной деструкции и структуры полимерных расплавов. Процесс поглощения кислорода в ходе деструкции контролируется как химическим строением полимера , так и структурой макромолекулярного клубка (D_f или b_d) [42; 43].

Как показано в главе 1, для полной и теоретически корректной характеристики фрактальных объектов необходимо использовать, как минимум, три размерности [45]. В настоящей монографии дан ряд методов, позволяющих решить эту задачу и определить следующие размерности: размерность евклидова пространства d, в котором протекает процесс окисления; фрактальная (Хаусдорфова) размерность макромолекулярного клубка D_f, описывающая его структуру; эффективная спектральная размерность , характеризующая связность клубка, а также степень временного (энергетического) беспорядка системы. Химическое строение полимера учитывается параметром , который рассчитывается аналитически и для ПААСО и ПАр не зависит от способа поликонденсации [46].

Для кривых  автозамедленного типа характерен процесс окисления, описываемый как псевдо-мономолекулярная реакция (реакция молекул оксиданта с реакционноспособными центрами макромолекул). Такая реакция описывается в общем виде уравнением (7.27) [36]. Вид указанного уравнения позволяет сделать следующее предположение: константа K определяет долю макромолекулярного клубка, подвергающуюся термоокислительной деструкции (чем больше K, тем выше и тем интенсивнее процесс деструкции), что дает [46]:

K = d - D_f.                                                            (8.24)

Затем можно окончательно записать уравнение (7.27) в форме, не содержащей эмпирических параметров, и поэтому пригодной для прогнозирования кинетических кривых  [46]:

.    (8.25)

Уравнение (8.25) включает все необходимые размерности: d, D_f и .

На рис. 8.19 в качестве примера приведено сравнение кривых , полученных экспериментально и рассчитанных согласно уравнению (8.25) для ПААСО-1 при трех температурах теплового старения Т_ст: 623, 673 и 723К (D_f = 2,78, 2,40 и 2,0, соответственно). Как можно видеть, уравнение (8.25) позволяет прогнозировать кривые   с достаточно высокой степенью точности [46].

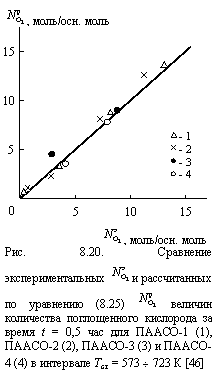
На рис. 8.20 показано сравнение величин  при t = 0,5 час. для всех рассмотренных ПААСО (см. табл. 6.1) в интервале Т_ст = 573 ¸ 723 К, полученных экспериментально и рассчитанных согласно уравнению (8.25). Вновь получено хорошее соответствие теории и эксперимента. Отметим, что оценка величины   согласно уравнению (8.1) для ПААСО-1 и ПААСО-2 при Т_ст = 623 К дала значения 103,3 и 67,1 моль О₂/осн. моль полимера, соответственно, что подтверждает эмпирический подгоночный характер этого параметра в трактовке уравнения (8.1) [46].

Таким образом, изложенные выше результаты продемонстрировали возможность физически корректного теоретического прогнозирования кинетических кривых   для полимерных расплавов при условии учета как химического строения полимера, так и физической структуры расплава. Последняя может быть количественно идентифицирована в рамках фрактального анализа и теории дробных производных. Полученное для целей прогнозирования кинетических кривых  уравнение не содержит эмпирических подгоночных параметров [46].