
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА
Обухов А. Г., Баранникова Д. Д.,
§4. Система уравнений газовой динамики при учете действия сил тяжести и Кориолиса
В параграфе, следуя [148] рассматривается квазилинейная система уравнений с частными производными – система уравнений газовой динамики. Эта система уравнений передает в дифференциальной форме основные законы природы – закон сохранения массы, закон сохранения импульса и закон сохранения энергии, а также учитывает основные законы термодинамики через использование конкретных уравнений состояния рассматриваемой движущейся сплошной среды.
При выборе конкретных масштабных значений скорости и расстояния система уравнений газовой динамики записывается в безразмерных переменных.
Решения системы уравнений газовой динамики в достаточно большом диапазоне изменения газодинамических характеристик – плотности, скорости, температуры, давления – адекватно описывают течения газа.
Основное отличие традиционно используемой системы уравнений газовой динамики от рассматриваемой в данном параграфе состоит в том, что здесь в системе присутствуют дополнительные слагаемые. С помощью этих дополнительных слагаемых учитывается действие силы тяжести и вращение Земли через сопутствующее этому вращению проявление силы инерции Кориолиса.
Для описания течения воздуха в тепловом восходящем закрученном течении, вращающемся вместе с Землей, вводится прямоугольная система координат с осями Ox, Oy, Oz, направленными на восток, север и вверх от поверхности Земли (рис. 2.1). При этом начало вращающейся системы координат лежит на параллели с широтой ψ. В прямоугольной системе координат постоянный вектор Ω угловой скорости вращения Земли задается формулой
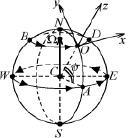
Рис. 2.1. Вращающаяся вместе с Землей прямоугольная система координат
Ω = (0, Ω2, Ω3) = (0, Ω cos ψ, Ω sin ψ), (4.1)
где Ω – модуль вектора Ω – определяется по формуле
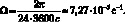 (4.2)
(4.2)
Если в системе координат Oxyz рассматривать движение идеальной сплошной среды, то уравнения движения имеют в векторной форме следующий вид, приведенный в [170]:
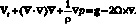 (4.3)
(4.3)
В векторном уравнении (4.3): t – время; V = (v1, v2, v3) – вектор скорости газа в декартовой системе координат Oxyz; ρ – плотность газа; p – давление газа; ∇ – оператор градиента по переменным x, y, z; g – вектор ускорения свободного падения
g = (0; 0; –g); g = const > 0.
Наличие в уравнении (4.3) двух слагаемых в правой части говорит о том, что на движение газа оказывают влияние, как земное притяжение, так и вращение Земли. Но при этом, сила Кориолиса работы не совершает из-за взаимной перпедикулярности v вектора скорости газа и вектора –2Ω×V. Благодаря наличию в правой части векторного уравнения (4.3) слагаемого –2Ω×V, в поток газа вносится дополнительный внешний импульс в виде вращательного момента. Именно этот внешний импульс – это внешний вращательный момент – и приводит к закрутке газа в придонной части теплового восходящего потока.
Особо следует обратить внимание на этот принципиальный момент: роль силы Кориолиса не в совершении работы (которую она и не совершает), а во внесении в поток внешнего дополнительного импульса.
Влиянием центробежного ускорения
–Ω×(Ω×r)
в уравнении (4.3) пренебрегается из-за его малости, но ускорение Кориолиса
ac = –2Ω×V = 2(Ω3v2 – Ω2v3)i – 2Ω3v1j + 2Ω2v1k
учитывается.
Векторное уравнение (4.3) равносильно трем скалярным уравненим для пяти искомых функций: ρ, v1, v2, v3, p. Чтобы получить замкнутую систему уравнений, необходимо, во-первых, учесть закон сохранения массы
ρt + V∙∇ρ + ρ div V = 0, (4.4)
который называется уравнением неразрывности, div – оператор дивергенции по переменным x, y, z.
Во-вторых, кроме закона сохранения массы необходимо также учесть закон сохранения энергии. Однако дифференциальная форма этого закона зависит от вида зависимости давления от двух других термодинамических параметров газа [149, 171].
Если рассматривается идеальный политропный газ и за независимые термодинамические параметры взяты плотность ρ и энтропия S, то давление газа задается соотношением
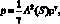 (4.5)
(4.5)
где A2(S) – энтропийная функция; γ = const > 1 – показатель политропы газа, а само уравнение (4.5) называется уравнением состояния. В этом случае дифферециальная форма закона сохранения энергии имеет вид [149]
St + V∙∇S = 0. (4.6)
Итак, в случае уравнения состояния (4.5) для пяти искомых функций: ρ, v1, v2, v3, S – имеется система из пяти скалярных уравнений (8.3), (8.4), (8.6),
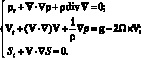 (4.7)
(4.7)
которая и представляет собой систему уравнений газовой динамики, отличающаяся от системы традиционного вида [149] учетом действия силы Кориолиса.
Если вместо функций ρ и S ввести другие функции [64, 65, 172–174]
σ = ρ(γ – 1)/2; s = A(s), (4.8)
то система уравнений газовой динамики с учетом силы Кориолиса приобретает вид:
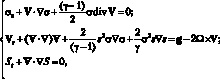 (4.9)
(4.9)
в которой присутствуют только целые положительные степени искомых функций σ, v1, v2, v3, s. При замене (4.8) скорость звука в газе  задается равенством c = sσ.
задается равенством c = sσ.
Систему уравнений газовой динамики с учетом силы Кориолиса – систему в виде (4.9) – удобно использовать при исследовании частного случая изэнтропических течений газа, т. е. когда S = const. Тогда функция s = A(s) тоже является константой и поэтому последнее уравнение в системе (4.9) выполняется тождественно. В изэнтропическом случае система уравнений газовой динамики в условиях действия силы Кориолиса становится системой из следующих четырех скалярных уравнений
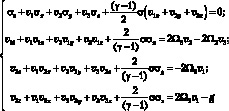 (4.10)
(4.10)
для четырех искомых функций σ, v1, v2, v3. Причем, если при введении безразмерных переменных будет выполняться равенство s = 1, то функция σ совпадает со скоростью звука c.
Часто отдельные области тепловых восходящих закрученных потоков или даже все потоки обладают осевой симметрией. В таких случаях удобнее рассматривать течение газа в цилиндрических координатах: r, φ, z.
В цилиндрической координатной системе уравнения газовой динамики (4.10) в условиях действия силы Кориолиса и изэнтропических течений политропного газа имеет следующий вид (2.1) [64]:
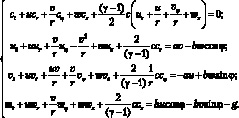 (4.11)
(4.11)
В системах (4.10), (4.11) с помощью масштабных размерных значений скорости, скорости звука, времени, и расстояния – u00, c00, t00, r00 стандартным образом вводятся безразмерные переменные:
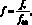
где f* и f00 – соответственно размерное и масштабное значения безразмерной величины f. При этом полагается, что
u00 = c00; 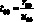 (4.12)
(4.12)
и тогда безразмерные значения констант Ω и g задаются следующим образом:
Ω = 7,27∙10–5 c–1∙t00; 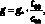
где g* = 9,8 м/с2.
В качестве независимых термодинамических переменных для записи уравнений состояния можно брать не плотность ρ и энтропию S, а плотность ρ и температуру T. В этом случае система уравнений газовой динамики принимает вид [64, 174]:
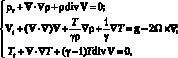 (4.13)
(4.13)
в которых также стандартным образом введены безразмерные переменные и тогда уравнение (4.8) для давления p и уравнение для внутренней энергии e идеального политропного газа в безразмерных переменных имеют вид
p = ρT; e = T (4.14)
и называются уравнениями состояния.
Применение системы уравнений газовой динамики (4.13) для описания сложных течений газа без учета физических эффектов вязкости и теплопроводности обосновано для определенных диапазонов изменения скорости течений и температуры. Однако во многих случаях при использовании системы уравнений газовой динамики часто возникают нефизические осцилляции. Для борьбы с этим явлением в вычислительные разностные схемы вводят дополнительные слагаемые или вычислительные приемы, которые сглаживают упомянутые осцилляции. С точки зрения теории уравнений с частными производными добавление этих слагаемых или использование специальных приемов означает, что неявно вводится учет диссипативных процессов. Эти приемы называются введением искусственной вязкости, поскольку они не несут явного физического смысла.
Для преодоления указанных вычислительных эффектов предлагается включать в систему уравнений газовой динамики члены, имеющие четкий физический смысл. Другими словами, учитывать вязкость и теплопроводность при выполнении фундаментальных законов сохранения массы, импульса и энергии, а также законы термодинамики через вид уравнений состояния. Предлагается использование полной системы уравнений Навье-Стокса, а не системы уравнений газовой динамики.