Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА

Обухов А. Г., Баранникова Д. Д.,

§5. Полная система уравнений Навье-Стокса при учете действия сил тяжести и Кориолиса

Полная система дифференциальных уравнений Навье-Стокса в условиях действия сил тяжести и Кориолиса в безразмерных переменных имеет вид [175, 148]:

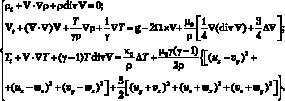(5.1)

Здесь ρ – плотность газа; u, v, w – проекции вектора скорости газа на декартовы оси; T – температура.

Система (5.1) в проекции на декартовы оси имеет вид:

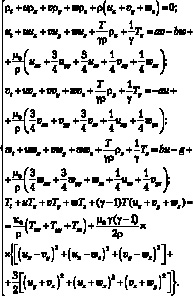(5.2)

В книгах [171, 65] приведена эта система, когда не учитывается действие силы Кориолиса. Благодаря наличию в правых частях уравнений движения – второго, третьего и четвертого уравнений системы (5.2) – слагаемых, отвечающих за присутствие ускорения Кориолиса, в поток газа, как и в случае системы уравнений газовой динамики, вносится дополнительный внешний импульс. Именно этот внешний импульс и приводит к закрутке вязкого теплопроводного газа в придонной части вертикального теплового восходящего потока.

В системе (5.2) при введении безразмерных переменных масштабные значения ρ00, T00, r00, u00, t00, p00, e00 связаны такими соотношениями [65]:

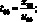p00 = Rρ00T00; e00 = cv0T00, (5.3)

где γ = 1 + R/cv0; R – универсальная газовая постоянная; cv0 – удельная теплоемкость.

Следовательно, за масштабные значения скорости, давления и внутренней энергии выбраны соответственно скорость звука, давление и внутренняя энергия газа с параметрами ρ00, T00. В работе в качестве масштабного значения скорости берется значение

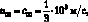
близкое к значению скорости распространения звука в воздухе при стандартных условиях [176], т. е. при ρ00 = 1,29 кг/м3, T00 = 288 К = 15 °С.

Безразмерные значения констант Ω и g приведены в предыдущем параграфе, а постоянные безразмерные значения коэффициентов вязкости μ0 и теплопроводности κ0 определяются следующими соотношениями:

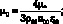
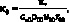
где μ*, κ* – размерные значения постоянных коэффициентов вязкости и теплопроводности. При исследовании течений вязкого теплопроводного газа часто вводят числа Рейнольдса и Прандтля:

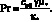
Тогда

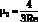и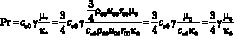 

и поэтому 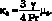Для воздуха Pr = 0,72, γ = 1,4 и тогда

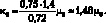
Система (5.2) имеет смешанный тип. Первое уравнение неразрывности образует гиперболическую часть системы [65, 66, 177]. Второе и третье уравнения движения и энергии составляют параболическую часть системы.