Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА

Обухов А. Г., Баранникова Д. Д.,

§6. Разностный метод построения решений полной системы уравнений Навье-Стокса

В данном параграфе приведено описание численных решений полной системы уравнений Навье-Стокса, которые моделируют течения в температурном закрученном восходящем потоке.

Для расчета нестационарных трехмерных течений в качестве расчетной области принимается прямоугольный параллелепипед, в котором строится равномерная прямоугольная сетка. Фрагмент трехмерной расчетной сетки узлов изображен на рис. 2.2. Расчеты ведутся по явной разностной схеме.

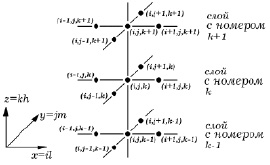
Рис. 2.2. Фрагмент трехмерной расчетной сетки узлов

Для полной системы уравнений Навье-Стокса при действии сил тяжести и Кориолиса (5.2), строится следующая разностная аппроксимация.

По известным начальным искомым функциям по явной разностной схеме вычисляются значения искомых функций во всех внутренних точках расчетной области в любой последующий момент времени. Данная вычислительная процедура для первого уравнения системы (5.2), записанного в скалярном виде

ρt + uρx + vρy + wρz + ρ∙(ux + vy + wz) = 0, (6.1)

представляется следующим образом. Воспользовавшись для аппроксимации производной по времени значениями функции плотности для двух последовательных моментов времени в узле (i, j, k)

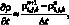(6.2)

а производные по пространственным переменным заменяя центральными разностями значений функций (рис. 2.2)

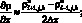
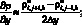
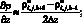(6.3)

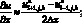
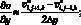
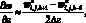(6.4)

перепишем уравнение (6.1) в виде:

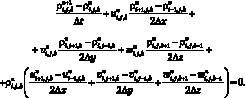(6.5)

Отсюда получим разностное уравнение для вычисления плотности газа во внутреннем узле (i, j, k) расчетной области

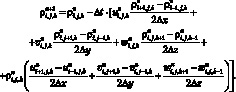(6.6)

Аналогично для второго уравнения системы (5.2) в скалярном виде

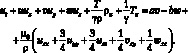(6.7)

Аппроксимируем производную по времени значениями функции скорости u для двух последовательных моментов времени в узле (i, j, k)

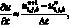(6.8)

а производные по пространству центральными разностями значений соответствующих функций

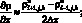
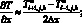(6.9)

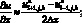
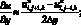
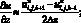(6.10)

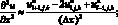
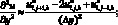(6.11)

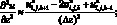(6.12)

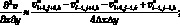(6.13)

(6.14)

Перепишем уравнение (6.7) в виде:

(6.15)

Отсюда получим разностное уравнение для вычисления первой компоненты скорости u во внутреннем узле (i, j, k) расчетной области

(6.16)

Для третьего уравнения системы (4.1), записанного в скалярном виде

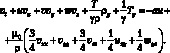(6.17)

Аппроксимируем производную по времени значениями функции скорости v для двух последовательных моментов времени в узле (i, j, k)

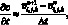(6.18)

а производные по пространству центральными разностями значений функций (рис. 5.2)

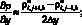
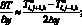(6.19)

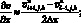
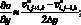
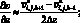(6.20)

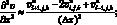
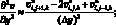(6.21)

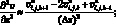(6.22)

(6.23)

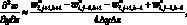(6.24)

перепишем уравнение (6.17) в виде:

(6.25)

Отсюда получим разностное уравнение для вычисления второй компоненты скорости v во внутреннем узле (i, j, k) расчетной области

(6.26)

Для четвертого уравнения системы (5.2), записанного в скалярном виде

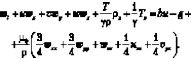(6.27)

Аппроксимируя производную по времени значениями функции скорости w для двух последовательных моментов времени в узле (i, j, k)

(6.28)

а производные по пространству центральными разностями значений функций (рис. 5.2)

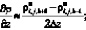
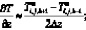(6.29)

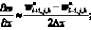
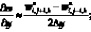
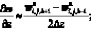(6.30)

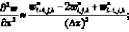
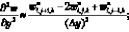(6.31)

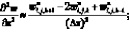(6.32)

(6.33)

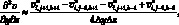(6.34)

перепишем уравнение (6.27) в виде:

(6.35)

Отсюда получим разностное уравнение для вычисления третьей компоненты скорости w во внутреннем узле (i, j, k) расчетной области

(6.36)

И, наконец, для пятого уравнения системы (5.2), записанного в скалярном виде

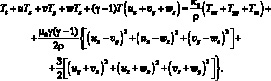(6.37)

Аппроксимируя производную по времени значениями функции температуры T для двух последовательных моментов времени в узле (i, j, k)

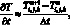(6.38)

а производные по пространству центральными разностями значений функций

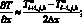
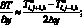
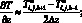(6.39)

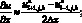
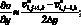
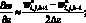(6.40)

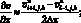
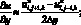
(6.41)

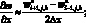
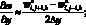
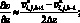(6.42)

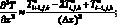
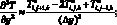(6.43)

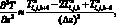(6.44)

перепишем уравнение (6.37) в виде:

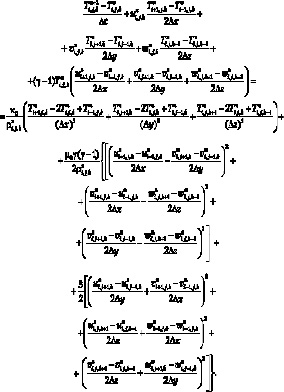(6.45)

Получим разностное уравнение для вычисления температуры T во внутреннем узле (i, j, k) расчетной области

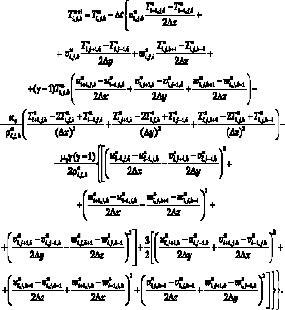(6.46)

Полученные выше соотношения (6.6), (6.16), (6.26), (6.36), (6.46) являются конечно-разностными уравнениями полной системы уравнений Навье-Стокса для численного расчета всех газодинамических функций (n + 1) временного слоя во всех внутренних узлах расчетной области в тройном вложенном цикле по трем пространственным переменным.

Использование формул (6.6), (6.16), (6.26), (6.36), (6.46) подразумевает, что расчет нестационарного трехмерного течения проводится с помощью явной разностной схемы с постоянным заданным шагом по времени Δt. При этом по пространственным координатам используется равномерная прямоугольная сетка с постоянными заданными шагами Δx, Δy, Δz соответственно. Расчетная область представляет собой прямоугольный параллелепипед, в основании которого находится квадрат с единичными сторонами: 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Высота параллелепипеда задается постоянной z = z0 и, следовательно, 0 ≤ z ≤ z0. Конкретное значение константы z = z0 выбирается разным для разных задач.

После этого, с учетом некоторых правил расчета газодинамических характеристик на границах расчетной области, рассчитываются значения всех искомых функций во всех граничных точках расчетной области. Алгоритм расчета подробно описан в седьмом параграфе.