Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ ВОСХОДЯЩИХ ЗАКРУЧЕННЫХ ТЕЧЕНИЙ ВОЗДУХА

Обухов А. Г., Баранникова Д. Д.,

§7. Начальные и граничные условия и их численная реализация

Точные аналитические решения заведомо передают конкретные, иногда очень специфические течения газа. И поэтому они помогают разобраться в газодинамической природе этих конкретных течений.

С другой стороны, точные решения служат тестами для проверки различных численных методик нелинейных систем дифференциальных уравнений с частными производными. И в этом смысле они очень востребованы при решении важных практических задач. В работах [178, 148] получены два точных аналитических решения системы дифференциальных уравнений газовой динамики и полной системы дифференциальных уравнений Навье-Стокса. Здесь использовалось одно из них [178].

Набор функций

u = 0; v = 0; w = 0, (7.1)

T0(z) = 1 – kz, (7.2)

где 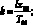l = 0,0065 К/м; x00 м; T00 = 288 °К

и

ρ0(z) = (1 – kz) v–1, (7.3)

где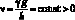

задают точное решение [178] системы (5.1) или (5.2) и могут быть использованы в качестве начальных условий описания сложных нестационарных трехмерных течений сжимаемого газа со свойствами вязкости и теплопроводности в тепловых закрученных потоках.

Функции (7.1)–(7.3) описывают начальное стационарное распределение покоящегося в поле силы тяжести воздуха, плотность и температура которого убывает с увеличением пространственной координаты z. Зависимости (7.2) и (7.3) приближенно описывают физически наблюдаемое распределение плотности и температуры воздуха. Тем не менее, до высоты в пять километров, они и качественно, и количественно хорошо передают данные натурных наблюдений за параметрами атмосферы Земли.

Набор пяти указанных функций, как аналитическое решение полной системы уравнений Навье-Стокса для бесконечного физического полупространства, используется в качестве начальных условий при моделировании нестационарных трехмерных течений вязкого сжимаемого теплопроводного газа в тепловых закрученных потоках для ограниченного пространства выбранной расчетной области.

Использование полной системы уравнений Навье-Стокса (5.1) добавляет трудности (и математические, и вычислительные) по сравнению с использованием системы уравнений газовой динамики (4.13). Для этих двух систем различным способом формулируются краевые условия для контактных поверхностей для вектора скорости газа [179]. Для системы дифференциальных уравнений газовой динамики (4.13) на таких контактных поверхностях нормальная компонента скорости берется равной нулю. Значения же двух других компонент вектора скорости ничем не ограничиваются. Это свойство для скорости течения газа называется условием непротекания.

Для течений вязкого газа, описываемых решениями полной системы уравнений Навье-Стокса (5.1), если по разные стороны от контактной поверхности имеются свои течения, то все компоненты векторов скорости на этой поверхности попарно совпадают. То есть частицы газа этих двух течений на контактной поверхности прилипают друг к другу из-за свойства вязкости. Если же течение газа по вторую сторону от контактной поверхности не рассматривается, то все три компоненты вектора скорости газа равны нулю. Такие граничные условия называются условиями прилипания.

Для течений газа в ограниченной области пространства граничные условия задаются из условия непрерывности потока или исходя из неизменности потока за пределами расчетной области – условия симметрии.

В первом случае краевые условия задаются с помощью линейной интерполяции из внутренней части расчетной области на ее границу. Во втором случае предполагается равенство нулю производных искомых функций в направлении нормали к граничной поверхности.

Численные решения полной системы уравнений Навье-Стокса находятся в расчетной области в виде прямоугольного параллелепипеда с длинами сторон x0, y0 и z0 вдоль осей Ox, Oy и Oz соответственно (рис. 2.3).

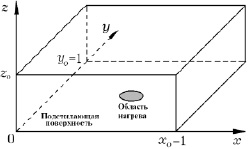
Рис. 2.3. Расчетная область в виде прямоугольного параллелепипеда

Правила вычисления газодинамических характеристик на границах расчетной области, описанные выше, для всех функций, характеризующих движущийся газ, имеют следущую численную реализацию.

1. Условие непротекания через грань расчетного параллелепипеда означает равенство нулю нормальной к соответствующей грани составляющей скорости газа [179]

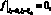(7.4)

где f – нормальная компонента вектора скорости к поверхностям ξ = 0, ξ = ξ0.

2. Условие непрерывности означает, что значения искомой функции на соответствующую грань расчетного параллелепипеда сносятся линейной интерполяцией по нормали к грани из внутренней части расчетной области, а именно [179]:

f(A) = 2f(B) – f(C), (7.5)

где f – значение искомой функции; A – узел, лежащий на грани; B и C – два ближайших к нему узла, расположенных внутри расчетного параллелепипеда на нормали к грани.

3. Условие симметрии означает, что на грани расчетного параллелепипеда полагаются нулевыми производные искомых функций в нормальном направлении к поверхности [179], то есть

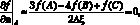(7.6)

где f – значение искомой функции; A – узел, лежащий на грани; B и C – два ближайших к нему узла, расположенных внутри расчетного параллелепипеда на нормали к грани; Δξ – расчетные шаги по трем пространственным направлениям. Из (7.6) получается такая расчетная формула

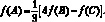(7.7)

Для температуры это условие означает теплоизолированность граничной поверхности. Локальный нагрев подстилающей поверхности моделируется соответствующими функциями, описанными в третьей главе.

Выбор соответствующих начальных условий и определенных правил вычисления газодинамических характеристик на гранях расчетной области является необходимым условием проведения численного решения полной системы уравнений Навье-Стокса при моделировании сложных нестационарных трехмерных течений сжимаемого газа со свойствами вязкости и теплопроводности в возникающих тепловых закрученных потоках.