
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Биологическая изменчивость и ее показатели
Биологические признаки подразделяют на качественные, например, окраска семян, окраска и форма коры, форма кроны дерева, диссимметрия хвои и шишек, наличие опушения у листьев, рассеченность края кроющих чешуй у шишек и т.д., которые ясно отличимы и дискретны, т.е. меняются очень резко, а также на признаки количественные, к которым относится высота, диаметр, объем ствола, объем кроны, толщина сучьев, угол отхождения ветвей от ствола, плотность хвои на 1 см длины побега и множество других признаков, которые имеют непрерывную изменчивость.
Изменчивость количественных признаков описывают следующими показателями.
1. Пределами (min, max, например, высота растений от 40 до 120 см).
2. Размахом (max-min, например, размах высоты растений 120 – 40 = 80 см).
3. Размахом в виде двух отклонений ∆ в максимальную xmax и минимальную xmin сторону от среднего арифметического xср:
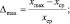

4. Средними отклонениями в сторону меньше и больше среднего:
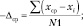
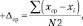
|
где хср – |
среднее значение показателя в выборке; |
|
хi – |
какое-либо одно значение (наблюдение, измерение); |
|
N1 – |
число наблюдений в части выборки меньше среднего значения, шт.; |
|
N2 – |
число наблюдений в части выборки больше среднего значения, шт. |
5. Среднеквадратическим или стандартным отклонением, обозначаемым чаще всего буквой «сигма»:
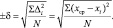 (1.1)
(1.1)
Из приведенных 5 показателей почему-то в биометрии для описания изменчивости используют чаще всего только показатели 1 и 5. Но почему же используют пятый показатель ±δ, самый сложный?
Все дело оказалось в том, что только с его помощью удалось описать распределения частот, подобных, например, распределению диаметров деревьев в так называемом «нормальном» насаждении (рис. 1.1).
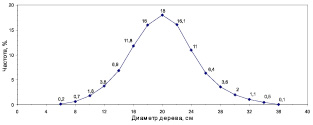
Рис. 1.1. Распределение по диаметру ствола 1 тыс. деревьев ели в нормальном насаждении 60-летнего возраста
Стандартное отклонение ±δ дважды включено в формулу, описывающую эту сложную по форме кривую, похожую на холм или гору:
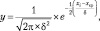 (1.2)
(1.2)
|
где y – |
частота какого-либо отклонения ∆ от среднего; |
|
π – |
число «пи» = 3,141…; |
|
e – |
основание натурального логарифма; |
|
δ – |
среднеквадратическое (стандартное) отклонение; |
|
xср – |
среднее (среднеарифметическое) значение выборки; |
|
xi – |
какое-либо значение признака. |
У стандартного отклонения ±δ есть совершенно замечательные свойства. Оказывается, если взять пределы xср ± δ, то в этих пределах окажется 68 % всех наблюдений, а в пределах xср ± 2δ их окажется 95 %. Для графика на рис. 1.1. средний диаметр равен 20 см, а стандартное отклонение ±δ = 4,7 см. Как раз около 5 % значений и остается за пределами 20 ± 2×4,7 см, если посчитать частоты в «хвостах» распределения – справа за пределами 29,4 см и слева менее 10,6 см (см. рис. 1.1).
В компьютере, после создания листа «Эксель», можно найти окно «функции», где есть еще окно «статистические функции». Там и можно найти программу для нахождения ±δ – под названием «СТАНДОТКЛ».
Как пример для понимания того, как рассчитать ±δ, покажем ее расчет на выборке из 25 однолетних сеянцев сосны по формуле (1.1) (табл. 1.1):
Таблица 1.1
Расчет стандартного отклонения в выборке из 25 сеянцев
|
Высота, см (xi) |
Число сеянцев (n) |
xi × n |
∆ = хi – хср |
Δ2 |
Δ2 × n |
|
2 |
1 |
2 |
–3 |
9 |
9×1 = 9 |
|
3 |
3 |
9 |
–2 |
4 |
4×3 = 12 |
|
4 |
5 |
20 |
–1 |
1 |
1×5 = 5 |
|
5 |
7 |
35 |
0 |
0 |
0×0 = 0 |
|
6 |
5 |
20 |
1 |
1 |
1×5 = 5 |
|
7 |
3 |
9 |
2 |
4 |
4×3 = 12 |
|
8 |
1 |
8 |
3 |
3 |
9×1 = 9 |
|
Сумма |
25 |
125 |
52 |
Для данных табл. 1.1 получаем среднюю высоту сеянцев 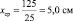 , и стандартное отклонение для высот в этой выборке из 25 растений
, и стандартное отклонение для высот в этой выборке из 25 растений
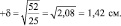
Но это еще не все замечательные свойства стандартного отклонения. За пределами xср ± 3δ теоретически может быть менее 1 % наблюдений, а за ±4δ их вообще не бывает, а если они объявятся – то это «чужаки» из другой популяции или «артфакты», которые следует отбросить при расчете среднего. И еще. Зная эти правила, всегда можно проверить расчеты по компьютеру, быстро разделив размах изменчивости (max-min) на 4 (то есть на пределы ±2δ) и получить грубые значения СТАНДОТКЛ:

Если выборка большая (более 60 значений) то тогда грубое значение ±δ получают делением размаха изменчивости на 6, так как большая выборка уже захватывает редко встречающиеся крайние значения и пределы полученной изменчивости увеличиваются до ±3δ, и можно делить размах уже на 6.
Для оценки величины изменчивости используют коэффициент вариации (вариацию), измеряемую в % от среднего и обозначаемую буквами CV:
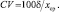
Для данных 1 тыс. измерений диаметра сосны, показанных выше на рис. 1.1, вариация равна 100×4,7/20 = 21,1 %, а для 25 сеянцев из табл. 1.1 она составит 100×1,42/5,0 = 28,4 %. Это обычный уровень вариации, характерный для большинства биологических признаков. Если вариация менее 15 %, то ее считают низкой, если более 35 % – повышенной (Мамаев, 1972).
Вариация становится равна стандартному отклонению, если среднее значение принять за 100 %, а все данные выразить в % от него. Это очень удобно для зрительного восприятия ряда распределения, в котором быстро определяют, например, самые толстые деревья, прибавив к 100 % двойную вариацию (или отняв ее от 100 % для определения самых тонких деревьев). Так, при среднем диаметре 20 см редко встречаются деревья с диаметром xср + 2CV = 100 + 2×21 = 144 %, т.е. 20×144 % = 28,8 см. Но они все-таки встречаются в 3,7 % случаев (см. рис. 1.1, правый «хвост» распределения). В лесной селекции их принято относить к так называемым «плюсовым деревьям».
