
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Критерий различия между средними значениями
Как видим, в биометрии важно доказать, что различие просто есть и обозначить % случаев его получения. Тогда как для обыденного сознания важен другой, более простой ответ на вопрос – на сколько различие больше? То есть подход у статистических методов совершенно иной. Он состоит в том, что различие, как расстояние между двумя средними на горизонтальной оси, измеряют не в сантиметрах, граммах или метрах, а в совершенно непривычных для нас единицах. Расстояние между средними измеряют в ошибках!
(Тут сразу вспоминаем весьма эвристичный мультфильм «38 попугаев», где длина удава составила 7 мартышек, 38 попугаев или 2 слоненка). То есть шкала для измерения чего-либо может быть разной. Разными получатся и оценки. Для измерения расстояния от х1 до х2 в ошибках, то есть статистического различия между ними, используют сумму ошибок этих средних значений:
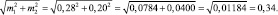
Если эту величину (0,34 см) представить как единицу на шкале измерения различий («сантиметр» на некоей «статистической» линейке по измерению расстояния между средними), то между ними будет уже не 6,0 – 5,0 = 1,0 см, как считает наше обыденное сознание, а (6,0 – 5,0)/0,34 = 2,94 неких единиц новой шкалы. Причем единицы эти меняются и зависят от объемов выборки в опытах. Эти единицы математик-биолог Стьюдент назвал «критерием t°». Критерий стали называть его именем и широко использовать для выяснения достоверности различия между выборочными средними:
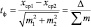 (2.2)
(2.2)
или, с другим обозначением средних величин
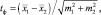
|
где tф – |
значение критерия Стьюдента в опыте (фактическое); |
|
Δ – |
разность между двумя средними величинами; |
|
|
сумма статистических ошибок средних величин. |
В нашем случае tф = 2,94. Много это или мало? Для ответа на этот вопрос Стьюдент составил специальную таблицу, где поместил пороговые значения t для разных вероятностей безошибочного прогноза, которые для краткости он назвал уровнями значимости и выделил три уровня для 90, 95 и 99 % безошибочных прогнозов:
t0,90; t0,95; t0,99 (табл. 2.1).
Сам же Стьюдент обозначал уровень значимости прогноза допускаемой ошибкой, которую также обозначал в виде подстрочного знака. Так, для 90 %-ного уровня обозначение было t0,10, для 95 %-ного – t0,05, которые иногда встречаются в некоторых пособиях по биометрии.
Таблица 2.1
Стандартные значения критерия t Стьюдента (по Лакин, 1973)
|
Степень свободы, шт. |
Уровень значимости (вероятность безошибочного прогноза) |
Степень свободы, шт. |
Уровень значимости (вероятность безошибочного прогноза) |
|||||
|
t0,90 |
t0,95 |
t0,99 |
t0,90 |
t0,95 |
t0,99 |
|||
|
1 |
6,31 |
12,7 |
63,7 |
9 |
1,83 |
2,27 |
3,25 |
|
|
2 |
2,92 |
4,30 |
9,92 |
10 |
1,81 |
2,23 |
3,17 |
|
|
3 |
2,35 |
3,18 |
5,84 |
15 |
1,76 |
2,15 |
2,98 |
|
|
4 |
2,13 |
2,78 |
4,60 |
20 |
1,72 |
2,09 |
2,85 |
|
|
5 |
2,02 |
2,57 |
4,03 |
30 |
1,70 |
2,04 |
2,75 |
|
|
6 |
1,94 |
2,45 |
3,71 |
60 |
1,67 |
2,00 |
2,66 |
|
|
7 |
1,89 |
2,36 |
3,50 |
100 |
1,66 |
1,98 |
2,63 |
|
|
8 |
1,86 |
2,31 |
3,36 |
1000 |
1,65 |
1,96 |
2,6 |
|
Вход в таблицу Стьюдента открывает показатель «степень свободы». Это, грубо говоря, сумма числа наблюдений в сравниваемых выборках. При малых выборках (менее 30) из суммы вычитают 2 единицы. Почему математики ее назвали степенью свободы – простым людям понять не дано (вероятно, имелось в виду некое «количество» свободы), но делать нечего, будем и мы ее так называть. Для случая с выборками по 100 растений степень свободы 100 + 100 = 200 и нужна последняя строка. В ней критерии t имеют значения 1,65; 1,96 и 2,6. А у нас получен tф = 2,94. Он больше стандарта для самого высокого уровня безошибочного прогноза в 99 %. Вообще, это хорошо для доказательства различия, но одновременно это и плохо для исследователя, так как объем выборки достаточно велик – 100 растений.
Выше мы делали расчеты для уровня прогноза в 95 %, т.е. для выборок по 25 растений, и получили просвет на рис. 2.3, то есть различие доказано. Поэтому еще уменьшим выборки, например, до 9 растений и получим:
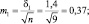
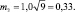
Откуда сумма ошибок составит
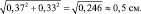
Поделим расстояние между средними, равное 1,0 см, на эту ошибку, равную 0,5 см, и получим tф = 1,0/0,5 = 2,0. Заходим в табл. 2.1 со своей степенью свободы, равной для выборок по 9 шт. 9 + 9 – 2 = 16. Для близкого значения 15 шт. находим в ней стандартные t0,90 = 1,76 и t0,95 = 2,16.
Сравнение полученного tф со стандартом обычно записывают в таком виде: tф = 2,0 > t0,90 = 1,76. Из этого сравнения следует вывод: различие достоверно на уровне 90 %-ного прогноза о существовании такого различия в действительности. Как видим, объем выборки, а значит, и трудозатраты на сбор семян и выращивание сеянцев можно сократить в 11 раз (со 100 до 9 измеряемых растений), и при этом доказать статистические различия между происхождениями «Кизел» и «Кунгур» в 9 случаях из 10. На самых первых этапах селекции, когда важно задействовать как можно больше вариантов опыта, такая пониженная точность вполне допустима, тем более, что далее испытания будут продолжены и оценки будут уточнены. Конечно, расчеты мы сильно упростили, но цель и смысл их становятся понятны – можно резко увеличить масштабы работ, изучая рост не 10–20, а 100–200 и более происхождений.
По сути, выше мы рассмотрели самую простую модель планирования объема выборки, основанную на подборе ее объемов для достижения заданного различия в 1,0 см между средними высотами. При этом мы брали выборки из 100, 50, 25 и 9 растений и показали, что различие в 1,0 см может быть доказано на разном уровне достоверности: в 99,5; 99; 95 и 90 % случаев. И какой объем выборки считать достаточным будут определять цели, стоящие перед исследователем.
Часто принимают уровень безошибочного прогноза в 95 % (t0,95), но этот уровень должен быть как-то обоснован, а не приниматься как догмат. На первых этапах селекции бывает иногда достаточен уровень и в 90 %.

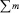 –
–