
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2. Развитие сосны в густых и редких культурах
При создании лесных культур расстояния между растениями в рядах часто сокращают до 0,5–0,6 м, поэтому рассмотрим влияние густоты на проявление закона Е. Л. Маслакова на реальных примерах. В Прикамье в 1950-е гг. сосну часто высаживали на старопахотные суглинистые почвы, где условия для нее оказались и благоприятны, и необычны, так как она эволюционировала в основном на песчаных почвах. Выдвинули гипотезу, что ее онтогенез в этих условиях происходит по-другому. Исследования проведены в культурах с расстоянием между рядами 2–2,5 м и в ряду от 0,55 до 0,75 м; 3 участка были на суглинистых и 3 – на супесчаных почвах. Срубали по 17–20 моделей на участке, по 4 модели
на каждый класс Крафта, всего 113. Значения переводили в относительные величины (% от среднего значения), после чего данные объединяли. Мерой соответствия роста служили возрастные корреляции между размерами деревьев в 4, 5, 7, 10 лет и их объемом в 29–40 лет.
Анализ показал, что корреляции в двух сравниваемых группах (культуры на суглинках и на супесях) оказались недостоверны, и поэтому гипотеза о различном онтогенезе сосны на песчаных и суглинистых почвах не подтвердилась. Непреднамеренно на этом же материале по фактору «расстояние между деревьями в рядах» удалось образовать две группы: 0,55–0,60 м (густые культуры) и 0,69–0,75 м (редкие культуры), по 3 участка в каждой. Оказалось, что в густых культурах корреляции для диаметров не превышают в среднем 0,47 даже к 10 годам, тогда как в редких они всегда были выше и достигали в среднем 0,60 в 4 года и 0,75 в 10 лет. Связи для высот были ниже и повышались не так стабильно (табл. 3.1).
Таблица 3.1
Коэффициенты корреляции объемов деревьев сосны в возрасте 29–40 лет с ростом растений в ранние годы (по Рогозину, 1983)
|
№ п/п |
С высотой (Н) |
С диаметром (Д) в возрасте, лет |
С условным объемом (Д2Н) в возрасте, лет |
|||||||||
|
4 |
5 |
7 |
10 |
4 |
5 |
7 |
10 |
4 |
5 |
7 |
10 |
|
|
Посадка в рядах через 0,55–0,60 м (густые) |
||||||||||||
|
55 |
||||||||||||
|
51 |
||||||||||||
|
61 |
||||||||||||
|
Среднее |
0,32 |
0,32 |
0,49 |
0,39 |
0,40 |
0,39 |
0,43 |
0,47 |
0,46 |
0,41 |
0,49 |
0,47 |
|
Посадка в рядах через 0,69–0,75 м (редкие) |
||||||||||||
|
56 |
||||||||||||
|
71 |
||||||||||||
|
72 |
||||||||||||
|
Среднее |
0,62 |
0,63 |
0,72 |
0,80 |
0,60 |
0,62 |
0,71 |
0,75 |
0,64 |
0,66 |
0,76 |
0,80 |
Различия между этими корреляциями оказались достоверны при Fф = 36,6 > F0,05 = 7,7. Эти различия можно объяснить усилением конкуренции в более густых культурах, которая приводит к тому, что отбор начинает действовать по-иному: быстрорастущие растения снижают рост и на их место в лидеры выходят толерантные к конкуренции особи.
Изменения в росте при повышении конкуренции является ответом популяции на изменение ценотической обстановки. При измерениях деревьев ответ этот предстает перед нами как их стремление изменять рост по каким-то внутренним причинам (и возникает соблазн назвать их «генетическими»). Конечно, это ответ генотипа и его реакция, но причина реакции лежит вне его. Генетические причины изменений в росте, безусловно, существуют. Однако необходимо вычленить их долю и сравнить с долей влияния факторов среды. В особенно редких культурах она может быть близка к генетически обусловленной величине. Поэтому крайне важно для ранней диагностики выяснить значения автокорреляций, свободных от конкурентного «шума».
Здесь можно сформулировать и предварительный ответ на вопрос, почему появляются «типы роста». Просто ответить: «потому что деревья разные по генотипам» нельзя. Ответ пока будет такой: «Причина появления различных типов роста – это воздействие ценотической обстановки и реакция генотипов на нее, видимая как изменения в росте; воздействие ценоза на каждое дерево различно, поэтому различен и их рост. Различия могут быть вызваны особенностями генотипа, но сила его влияния пока не установлена».
Вопрос этот сложен. В лесной селекции сроки оценки элитности лесных пород все еще неясны, не установлена сила влияния генотипа на типы роста, неясен рост дерева в условиях повышенной и оптимальной конкуренции.
Когда выяснилось, что усиление конкуренции влияет на ранговый закон Е. Л. Маслакова, то мы представили его действие в более понятной форме – как вероятность наступления желательного для нас события (формирование дерева с размерами выше среднего). Для этого были построены точечные диаграммы (поля корреляции) для диаметров стволиков в ранние годы и объемов их стволов в 29–40 лет. Далее для анализа вероятностей поля разделили горизонтальной линией на 2 ранга по объему стволов и вертикальной линией – на 2 ранга по диаметру. В итоге получилось 4 сектора, и по верхним секторам можно рассчитать вероятности наступления желательного для нас события, а именно, формирование крупного дерева (рис. 3.3).
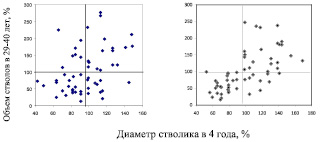
Рис. 3.3. Диаметр стволика в 4 года и объем стволов в 29–40 лет в густых (слева) и в редких (справа) культурах сосны
Эти поля имеют корреляции, равные 0,40 для густых и 0,60 – для редких культур (см. средние значения в табл. 1.1).
Сразу обращаем внимание на почти пустой верхний левый сектор на правом графике, что означает, что в редких культурах у тонких в 4 года стволиков почти нет шансов сформировать крупные деревья: всего 1 дерево достигло объема ствола 100 %, что дает вероятность формирования крупных деревьев 1/25 = 0,04. Напротив, в густых культурах 27 тонких стволиков сформировали 7 крупных деревьев (вероятность 7/27 = 0,26). Из толстых стволиков эти вероятности были выше и достигли для 4 лет 62–68 %, а для 10 лет 69–74 %. Их можно представить и в виде диаграмм (рис. 3.4).
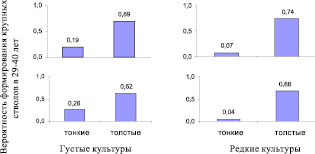
Рис. 3.4. Вероятность формирования крупных стволов из тонких и толстых стволиков в 4 года (внизу) и в 10 лет (вверху)
