Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.1.1. Уравнения движения реальной атмосферы в поле массовых сил

Особенностью учета орографии в численных моделях является то, что он тесно связан с включением горизонтальной неоднородности массовых сил посредством определения потенциала силы тяжести в реальной атмосфере. Возьмем уравнения движения в векторной форме Громеко-Ламба для системы координат, вращающейся вместе с Землей:

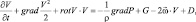
где  – вектор угловой скорости вращения Земли; D – вектор диссипативных сил; G = G(q1, q2, q3) – вектор ускорения силы тяжести; V = V(v1, v2, v3) – вектор скорости; v1, v2, v3 – компоненты вектора скорости по осям криволинейной системы координат q1, q2, q3:

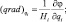
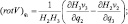
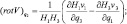
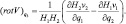
Введем в качестве дополнения до геодезической широты α, тогда q2 будет геодезической долготой λ, а q3 направим по нормали к эллипсоиду Земли. Расстояние любой точки M от ее проекции на поверхность эллипсоида M1 будем измерять высотой ξ.

Связь абсолютных координат с вновь введенными осуществляется посредством следующих формул:

x = [а(α)∙sinθ + ξ∙sinα] cosλ;

y = [а(α)∙sinθ + ξ∙sinα] sinλ;

z = а(α)∙cosθ + ξ∙cosα, (2.1)

где θ = θ(α) – дополнение до геодезической широты. Разность между геодезической и географической широтами представляется формулой:

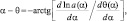(2.2)

а коэффициенты Ламэ можно записать в следующем виде:

H1 = a(α)∙h1(α, ξ); H2 = a(α)∙h2(α, ξ) sinα; H3 = 1, (2.2′)

где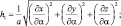

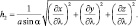
Воспользовавшись (2.1) и (2.2), для h1, h2 получим:

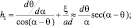
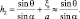(2.3)

Предложенная система координат ортогональна

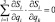(j ≠ k),

где S1 = x, S2 = y, S3 = z.

Если за эту поверхность принять явно эллипсоид вращения, то все формулы приводится более простому виду:

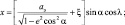(2.4)

(2.5)

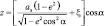(2.6)

В эти формулы входят два параметра, определяющие эллипсоид: €э – радиус Земли в плоскости экватора и квадрат эксцентриситета 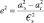. Эксцентриситет легко можно выразить через другую удобную характеристику эллипсоида – через сжатие S 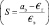следующим образом: e2 = 2S – S2. Найдем радиус-вектор точки M1(a).

В меридиональном сечении для эллипсоида имеем:

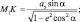
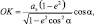
откуда

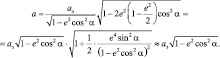
Тогда

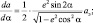
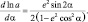(2.7)

Связь между геоцентрической и геодезической широтами осуществляется посредством выражения:

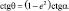(2.8)

Дифференцируем это выражение по α, кроме того, из (2.2) следует:

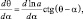(2.9)

а из (1.8)

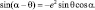(2.10)

Тогда 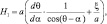и подставляя сюда (2.9) и используя (2.7), получим:

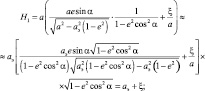(2.11)

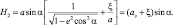(2.12)

Итак, в практических задачах решение (2.2) с коэффициентами Ламэ из (2.2′) представляют определенные трудности, а нами для коэффициентов Ламэ получены, с точностью до величин e4, очень простые выражения, по форме совпадающие с коэффициентами Ламэ для сферы.

Полученные уравнения удобно использовать при описании движения реальной атмосферы в поле массовых сил и при определении связи между геоцентрической и геодезической широтами для объективной оценки экологической обстановки окружающей среды.