Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.1.3. Уравнения баланса влаги в атмосфере

Рассмотрим двухфазную среду (гидромеханики многофазных сред [43, 61]), состоящую из влажного воздуха, имеющего плотность ρ, и водных капель, содержание которых будем оценивать удельной водностью δ. Введем для двухфазной среды плотность и имеем соотношение

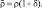(2.15)

В облачной фазе различают две группы капель (две компоненты). Первая группа содержит капли крупных размеров (гидрометеоры), которые не вовлекаются целиком восходящим потоком и имеют значительную скорость оседания 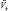, удельная водность этой группы капель δk, определяемое как отношение плотности крупных капель к плотности влажного воздуха. Во вторую группу войдут мелкие капли, которые полностью вовлекается основным потоком. Таким образом, облачная среда во влажном воздухе представляет собой гетерогенную или многофазную смесь (в данном случае трехфазную). В гетерогенной смеси каждая фаза имеет лишь часть объема смеси, вследствие чего полный объем равен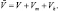

Кроме того, температура, скорость, давление, энергия, плотность удовлетворяют условию аддитивности по плотностям фаз. Рассмотрим гетерогенную смесь в виде совокупности трех фаз заполняющих один и тот же объем. В результате в каждой точке пространства, занятого смесью, можно ввести средние плотности ρ, ρm, ρk характеризующие массу фазы в единице объема смеси, средние скорости движения фаз Vb, Vm, Vk и т.д., а также выписать уравнения сохранения массы, моментов и энергии для каждой составляющей смеси, куда будут включены члены, описывающие межфазовые взаимодействия (массовые, силовые и энергетические). В облачной среде, состоящей из двух компонент, проходят процессы оседания, коагуляции, динамического слияния и испарения. Обозначим через Vk скорость движения крупных капель, V – осредненная по массе скорость движения всей среды, то скорость оседания или диффузии этой фазы 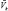будет равна [61, 92]:

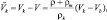(2.16)

а уравнение неразрывности примет вид:

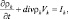(2.17)

где I, Im – отнесенная к единице массы скорость прироста соответствующей фазы (влажного воздуха и мелких капель) за счет микрофизических процессов. Поток V характеризует движение всей смеси. При рассмотрении крупных капель (гидрометеоров) следует учесть, что их скорость движения будет отличаться от скорости движения, например, мелких капель.

Или 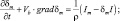(2.18)

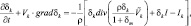(2.19)

где 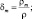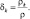(2.20)

Выражения (2.18) и (2.19) – общие уравнения концентрации, описывающие баланс каждой компоненты облачной среды. Для двухкомпонентной облачной среды:

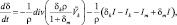(2.21)

где δ = δm + δk;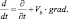

Первый член в правой части описывает диффузию гидрометеоров за счет гравитационного оседания, а второй должен включать скорость конденсации и вовлечения. Второй член в (2.21) можно представить в виде:

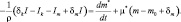(2.22)

В уравнении (2.18) правую часть запишем следующим образом:

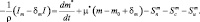(2.23)

Здесь первый член в правой части описывает количество водяного пара путем конденсации, переходящего в капельное состояние, второй – описывает изменения водности в результате вовлечения.  – установившийся процесс роста крупных капель за счет уменьшения мелких путем перекачки водяного пара от мелких к крупным каплям:

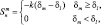
где K – степень роста крупных или убывания мелких капель в единицу времени; δl – значение удельной водности, после достижения которой мелкие капли становятся гидрометеорами;  – изменение удельной водности за счет слияния.

По Кеслеру [257] эмпирическая зависимость:

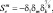(2.24)

где δ1 – параметр, описывающий собирательную способность капель и концентрацию собирающих крупных капель, 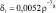. Для использования в крупномасштабных моделях можно положить приближенно:

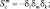(2.25)

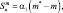(2.26)

где 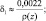α1 – эмпирический параметр, описывающий скорость испарения мелких капель;  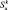– испарение крупных капель.

Из (2.22) для крупных капель будем иметь:

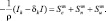
Уравнение неразрывности для смеси влажного воздуха и облачной среды:

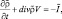(2.27)

где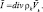

Если отсутствует процесс гравитационного оседания, то уравнение имеет вид:

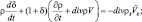(2.28)

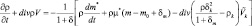. (2.29)

Пологая, что диффузия гидрометеорной компоненты происходит только благодаря гравитационному оседанию, тогда:

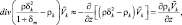(2.30)

где 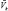 – положительна и направлена к земле согласно [41].

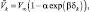(2.31)

где α, β – эмпирические параметры; V∞ – предельная скорость оседания.

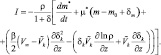(2.32)

Выпишем уравнения для отношения смеси:

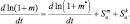(2.33)

Берем уравнение неразрывности в следующем виде:

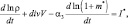(2.34)

где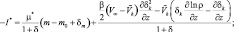

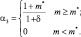
При отсутствии конденсации и вовлечения мы приходим к уравнению неразрывности без источников для влажного однородного воздуха

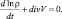(2.35)

Горизонтальные компоненты скорости движения гидрометеоров совпадают с движением влажного воздуха и мелких капель облачной фазы, а вертикальная компонента скорости влажного воздуха и гидрометеоров различны. Фигурирующая в уравнениях средняя вертикальная скорость движения среды определяется как взвешенная по плотностям фаз и компонент вертикальная скорость. Wb вертикальная скорость движения мелкой компоненты облака и влажного воздуха, тогда средняя вертикальная скорость W будет равна: