Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.2.2. Прогностические уравнения для сглаженных значений метеорологических элементов в сжимаемой атмосфере
Рассмотрим уравнения гидротермодинамики сжимаемой атмосферы для сглаженных величин с использованием гипотезы о линейной связи между одноточечными моментами и осредненными характеристиками движения.
Рассмотрим систему уравнений гидротермодинамики для сжимаемой атмосферы в виде [22]:
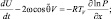(2.54)
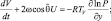(2.55)
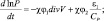(2.56)
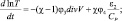(2.57)
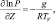(2.58)
где U, V, W – компоненты скорости на оси координат x, y, z; 
– дополнение до географической широты; ω – угловая скорость вращения Земли.
Пусть 
где 
и 
суть постоянных величин.
Видоизменим уравнения (2.67), (2.68), введя вместо P и T функции π и θ: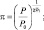 
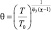(T0, P0 – константы, имеющие размерности соответственно температуры и давления).
Тогда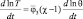 
и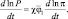 
И, следовательно,
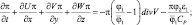(2.59)
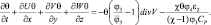(2.60)
Правые части этих уравнений обращаются в ноль в адиабатической атмосфере и было бы более удобным ввести вместо π и θ потенциальную температуру и затем уравнение для последней свести к дивергентной форме.
Имея, что
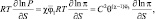
где S = (x, y),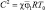 
, уравнения движения примут вид:
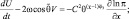(2.61)
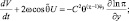(2.62)
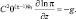(2.63)
Введем осредненные по времени характеристики 
, 
, 
, 
, 
, 
связанные с мгновенными величинами соотношениями:
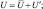
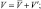
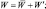
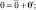
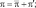
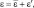
где штрихами обозначены отклонения от осредненного состояния.
Используя рейнольдсовские постулаты осреднения и применив операцию осреднения, получим:
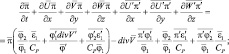(2.64)
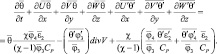(2.65)
Последние три члена в левых частях представляют собой дивергенцию турбулентных потоков энергии и тепла, обусловленные пульсациями давления и температуры. Воспользуемся гипотезой о линейной зависимости между векторами турбулентных потоков по осям координат и осредненными характеристиками [55] и запишем формально:
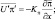
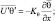
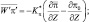
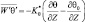и т.д. (2.66)
где π0, θ0 – стандартные значения π и θ; Kπ, Kθ,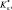 
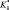– коэффициенты турбулентности, которые сами в свою очередь зависят от характеристик осредненного движения.
В этом смысле рассматриваемая система не является замкнутой и требуется, как известно, привлечь еще какие либо дополнительные гипотезы относительно поведения коэффициентов турбулентности. Используя (2.66), уравнения (2.64), (2.65) можно записать в следующем виде:
(2.67)
(2.68)
где Sπ, Sθ содержат все оставшиеся члены.
Не останавливаясь на физических свойствах характеристик Sπ, Sθ, предполагая, что они в первом приближении могут быть опущены ввиду очевидной относительной малости.
Уравнения (2.67), (2.68) дополним соображениями, определяющими коэффициенты Kπ, Kθ. Для крупномасштабных процессов допустимо предположение [50], что Kπ = const, Kθ = const и, согласно закону Ричардсона-Обухова, пропорциональны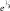 
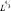, где e – средняя для всей атмосферы диссипация кинетической энергии (5 эрг/г∙с) (L – масштаб возмущений).
В результате получим:
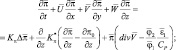(2.69)
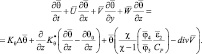(2.70)
Перейдем теперь к рассмотрению уравнений движения. Умножим (2.61) на π, а (2.59) на U и сложим эти два уравнения. После применения операции осреднения и введения линейной гипотезы для напряжений, получим:
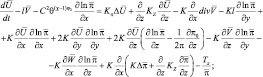(2.71)
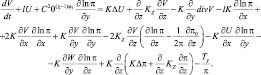(2.72)
Первые два члена правых частей обычно входят в уравнения при условии несжимаемости атмосферы. Все остальные слагаемые появились благодаря учету сжимаемости. Здесь введены безразмерные параметры:
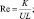
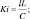
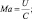
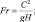
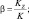
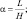
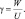
Уравнения (2.71), (2.72), (2.58), (2.69), (2.70) при заданных внешних радиационных притоках тепла и соответствующих начальных и краевых условиях служат системой для определения осредненных метеорологических элементов.