Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

2.3.1. Вывод уравнения для вертикальной скорости в насыщенной атмосфере

Вывод уравнения для вертикальной скорости в насыщенной атмосфере удобно осуществить с помощью уравнений (2.49) и (2.52) и введя в эти уравнения диссипативные члены εθ, επ и εm получим:

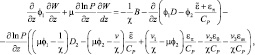(2.82)

где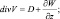

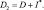
Это описывает баланс между вертикальными движениями, горизонтальной бароклинностью, плоской дивергенцией и притоками тепла. Предполагая все факторы, кроме W, известными, уравнение (2.82) можно рассматривать как дифференциальное уравнение для определения вертикальных движений. Это уравнение второго порядка и, следовательно, его необходимо дополнить двумя краевыми условиями. На нижней границе возьмем:

z = 0, W = W0(x, y). (2.83)

Плоской Земли W0 = 0. На верхней границе:

при z → ∞ 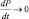, (2.84)

или p → 0. (2.85)

Уравнение (2.82) можно привести к иному виду. Умножая уравнение на 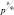, получим после несложных преобразований:

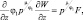(2.86)

где F – правая часть уравнения (2.82).

Теперь решение уравнения (2.86) с учетом краевых условий (2.83), (2.85) нетрудно выписать в квадратурах.