
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.4.2. Конечно-разностная схема решения задачи
Поскольку левая часть системы (2.117)–(2.119) содержит только производную по ξ, то она решается независимо от прогностической части модели. Рассмотрим пространственно-временную сетку, по которой будет решаться задача.
В плоскости x, y, t производные заменяются центральными разностями по аналогии с работой [289]. Атмосфера разбивается по ξ на равномерные слои с Δξ = 0,2. Помимо основных уровней вводятся промежуточные уровни. Основные параметры задачи (U, V, π, Г) зафиксированы на основных уровнях (l = 2, 3, 4, 5), кроме l = 1 (ξ = –0,1), который является фиктивным, а вместо него носителем информации выбран промежуточный уровень l = 3/2 (ξ = 0).
В формуле (2.115) принято a = 10–4 м–1, b = 0,9. Соответствие выбранных уровней геометрическим высотам представлено в табл. 30.
Таблица 30
Соответствие выбранных уровней геометрическим высотам представлено
|
l |
ξ |
Z(м) |
l |
ξ |
Z(м) |
|
1 |
–0,1 |
–1176,58 |
4 |
0,5 |
8119,31 |
|
2 |
0,1 |
1176,58 |
5 |
0,7 |
15050,78 |
|
3 |
0,3 |
4049,65 |
6 |
0,9 |
∞ |
Диагностическая система решается для промежуточных точек горизонтальной сетки. Уравнения (2.117)–(2.119) записываются в конечных разностях по схеме Г.И. Марчука [117]. Методом обычной прогонки решается следующее трехточечное уравнение (подробный вывод приведен в работе [271]):
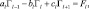 l = 2, 3, 4, 5, (2.121)
l = 2, 3, 4, 5, (2.121)
где 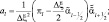
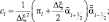
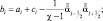
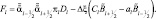
Краевые условия согласно (2.116а) будут выглядеть следующим образом:
Γ6 = 0; 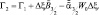 (2.122)
(2.122)
Решение находится в точках 1, 2, 3, 4, 5, а 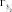 определяется как среднее между Γ1 и Γ2. При практической реализации модели в правой части использовалась не чистая плоская дивергенция, а ее отклонение от среднего по вертикали значения. Эта операция на практике исключает не реальное развитие процессов, вызванное завышением роли дивергенции верхних уровней, ввиду выбранной вертикальной структуры сетки.
определяется как среднее между Γ1 и Γ2. При практической реализации модели в правой части использовалась не чистая плоская дивергенция, а ее отклонение от среднего по вертикали значения. Эта операция на практике исключает не реальное развитие процессов, вызванное завышением роли дивергенции верхних уровней, ввиду выбранной вертикальной структуры сетки.
После того, как задача (2.121), (2.122), (2.123) будет решена, рассматривается прогностическая задача. Следуя работе [181], введем обозначения для конечных разностей:
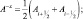
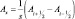 и т.д.
и т.д.
Запишем теперь прогностическую часть модели в следующем виде:
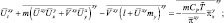
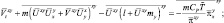 (2.123)
(2.123)
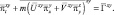
Область решения занимает ограниченную территорию с сеткой 24×20 точек с шагом d = 381 км на карте меркаторской проекции. На боковых границах ставятся краевые условия. Они являются неестественными и поэтому подбор соответствующих краевых процедур представляет собой трудную экспериментальную задачу. В результате большого числа экспериментов были получены наилучшие результаты с закрепленными (U, V, π – постоянны) краевыми значениями и с фильтрирующей процедурой, сглаживание применялось через каждые 2 часа по отношению к самим прогнозируемым величинам. На этом следует остановиться несколько подробнее. Формально сглаживание производилось по формулам [238]:
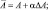
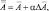 (2.124)
(2.124)
где Δ = ()i,j–1 + ()i,j+1 + ()i+1,j + ()i–1,j – 4()i,j.
Если рассмотреть только первый шаг этой процедуры, то он эквивалентен приближенному (одной итерации) учету горизонтально макротурбулентности в уравнениях системы (2.124). В зависимости, по отношению к каким полям делается сглаживание, можно говорить в данном случае, по полуявном учете горизонтальной макротурбулентности, если сглаживаются исходные поля, и по полуявном, если сглаживаются спрогнозированные поля. При этом
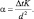
При Δt = 900 с, K = 106 и d = 381 км должно быть α = 0,0066. Практически использовалось α = 0,125, но сглаживание применялось каждые 16 шагов. Суммарный эффект при этом получался одинаковый, а затраты машинного времени меньше, чем если бы сглаживание производилось каждый шаг с α = 0,001. Поскольку мы пользовались двушаговой процедурой, уменьшающей сглаживание волн размером большим, чем 2d, то принятый процесс можно считать эквивалентным учету горизонтальной макротурбулентности с K < 106 м2∙с–1.
Следует иметь также в виду, что в процессе прогноза из-за сильного влияния краев и несогласованности начальных данных, начинают проявляться гравитационные волновые возмущения, искажающие метеорологические поля, поэтому в модель введен переменный по времени средней дивергенции, скорости потока и орографии. Это достигалось путем выбора следующего выражения для α:
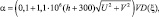 (2.125)
(2.125)
где VD(ξ) – эмпирическая функция высоты; h – высота земной поверхности в метрах.
На каждом шаге вычисляется средняя квадратичная дивергенция и в зависимости от ее величины изменяется чистота сглаживания с α, определенным по (2.125). Таким образом, в модели введена имитация переменного по x, y, ξ, t коэффициента горизонтальной турбулентности.