Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
2.4.5. Организация оперативных расчетов. Результаты испытания
Описанная модель S – 1 вначале была проверена на тестовом расчете с искусственными начальными данными. Расчет проводился с циклическими краевыми условиями по x и давал реалистические результаты в течение 3-х суток прогноза.
Для определения начального поля π на фиксированных геометрических уровнях, вводились данные геопотенциальных высот на стандартных изобарических поверхностях 1000, 700, 500, 300 и 100 мбар. Эти данные интерполировались на стандартные высоты модели с помощью квадратичной интерполяции. Результаты прогнозов для удобства анализа и использования затем опять переинтерполировались на стандартные изобарические поверхности. Прогностические карты геопотенциала выдаются на 5 поверхностях: 1000, 700, 500, 300, 1000 мбар и горизонтальных составляющих ветра на высотах: уровень моря, 1, 4, 8, 15 км.
Модель глобальной циркуляции основана на системе примитивных уравнений гидротермодинамики в квазистатическом приближении. Уравнения те же, что и для предыдущей модели, но записаны в сферических координатах [169]:
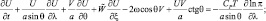 (2.142)
(2.142)
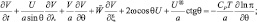 (2.143)
(2.143)
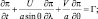 (2.144)
(2.144)
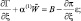 (2.145)
(2.145)
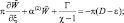 (2.146)
(2.146)
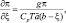 (2.147)
(2.147)
где λ, θ – долгота и дополнение до широты места; U, V – горизонтальные компоненты ветра; U – направлена к востоку; V – к северу.
Остальные обозначения остаются прежними и, кроме того,
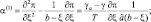 (2.148)
(2.148)
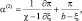 (2.149)
(2.149)
где γa, γ – адиабатический и обычный вертикальные градиенты температуры, 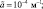
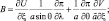 (2.150)
(2.150)
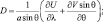 (2.151)
(2.151)
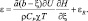 (2.152)
(2.152)
где H – турбулентный поток тепла; εR – внешние притоки тепла за счет радиации и других источников.
По вертикали система требует двух условий. Выберем их следующим образом:
Γ → 0 при ξ = 0,9 (z → ∞);
W = W0(θ, λ) при ξ = 0 (z = 0).
Здесь W0(θ, λ) представляют собой вертикальные движения у земной поверхности, обусловленные орографическими и фрикционными эффектами и определяются аналогично (2.131) и (2.132).
Решение ищется на сферической сетке точек с параметрами Δλ = 10° и Δθ = 7,5°. По вертикали точки располагается так, как показано на рис. 2.3. Основные функции: U, V и π определены в основных узлах сетки. Значения  определяются на дробных уровнях. Основные уровни l = 1, 2, 3, 4, 5 располагаются на геометрических высотах 0; 1176; 4050; 8119 и 15051 м соответственно.
определяются на дробных уровнях. Основные уровни l = 1, 2, 3, 4, 5 располагаются на геометрических высотах 0; 1176; 4050; 8119 и 15051 м соответственно.
Рассмотрим вначале диагностическую часть. Конечно-разностное представление уравнений (2.145) и (2.146) делается аналогично тому, как сделано для локальной модели. В результате получаются по l трехточечное уравнение следующего вида:
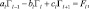 l = 2, 3, 4, 5, (2.153)
l = 2, 3, 4, 5, (2.153)
где 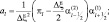
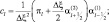
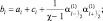
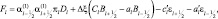
где 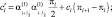
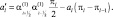
Краевые условия, согласно (2.153), будут выглядеть методом прогонки. Решения находятся на уровнях l = 1, 2, 3, 4, 5 в центрах горизонтальной сетки.
Определим конечно-разностную аппроксимацию дифференциальных операторов В и D. Нумерацию точек по λ будем осуществлять с запада на восток и обозначать индексом i, а по θ – с севера на юг и обозначать буквой j. Введем обозначения:
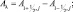
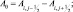
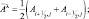
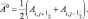 (2.154)
(2.154)
Кроме этого, обозначим:
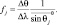
Тогда для B и D можно записать:
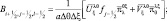 (2.155)
(2.155)
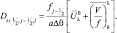 (2.156)
(2.156)
Опишем методику вычисления вертикальных движений воздуха. Наиболее простой путь определения  основан на использовании уже вычисленных значений Г с помощью уравнения (2.146). Запишем это уравнение в целых точках l следующим образом:
основан на использовании уже вычисленных значений Г с помощью уравнения (2.146). Запишем это уравнение в целых точках l следующим образом:
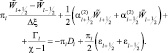
Отсюда:
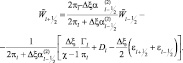 (2.157)
(2.157)
Краевое условие ставится на нижнем, первом дробном уровне l = 3/2. Предполагается, что вертикальная скорость на этом уровне складывается из фрикционных и орографических движений.
Перейдем к рассмотрению эволюционной задачи. Уравнения (2.142), (2.143) и (2.144) обрабатываются следующим образом. В левую часть переносятся члены с частной производной по времени и все линейные члены, которые представляются как средние по времени выражения на интервале 2Δt. Левая часть уравнений записывается в центральный момент времени и усредняется по четырем окружающим точкам. В результате такой обработки получим:
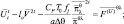
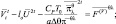 (2.158)
(2.158)
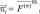
где l0 – параметр Кориолиса при θ = 45°; T0 – средняя температура в атмосфере.
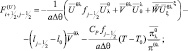
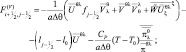
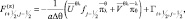
где 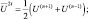
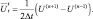 (2.159)
(2.159)
Из (2.159) следует, что:
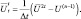
Подставим это выражение в уравнения системы (2.169). Тогда:
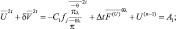
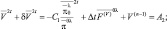
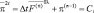
где δ = l0Δt; 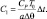
Первые два уравнения решаются относительно 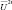 и
и 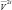 с использованием вместо π его значения из третьего уравнения. В итоге получим:
с использованием вместо π его значения из третьего уравнения. В итоге получим:
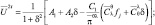
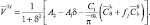 (2.160)
(2.160)
После этого определяются:
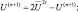
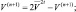
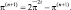
Значения метеоэлементов на полюсе, который представлен в модели 36 точками, вычисляются по методике Курихара. Значение π на полюсе находится как среднее значение на ближайшей широте. Всем 36 точкам «полюса» приписывается это значение. Ветер на 36 точках «полюса» вычисляется следующим образом. Вектора скоростей на ближайшей широте (j = 2) в каждой точке векторно переносятся в полюс, складываются и усредняются. Полученный таким образом результирующий вектор затем снова проектируется в 36 точках «полюса» на направление λ и на проходящее через каждую точку направление меридиана. Полученные таким образом компоненты U, V в 36 точках, представляющие полюс, используются затем в дальнейших расчетах.
Для ликвидации линейной неустойчивости, возникающей вблизи полюса из-за большого числа точек вдоль круга широт, применялась процедура фильтрации вдоль круга широт, в которой число от фильтрованных гармоник обратно пропорционально 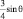 .
.
Динамический орографический эффект осуществляется через вертикальные движения. Орографические вертикальные движения вычисляются из выражения 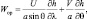 в конечных разностях принимает вид:
в конечных разностях принимает вид:
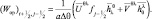 (2.161)
(2.161)
Вертикальные движения за счет трения о поверхность Земли находятся из выражения:
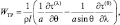 (2.162)
(2.162)
где 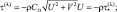 (2.163)
(2.163)
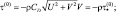
ρ – плотность воздуха.
Скорость ветра в (2.163) берется на уровне моря. Конечно-разностный аналог выражения (2.162) с учетом (2.163) имеет вид:
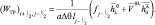 (2.164)
(2.164)
Здесь 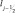 – переменная для всех j < 8 и
– переменная для всех j < 8 и 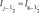 для j ≥ 8. Вычисленные значения WТР и WОР приписываются уровню
для j ≥ 8. Вычисленные значения WТР и WОР приписываются уровню 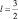 и складываются.
и складываются.
Таким образом,
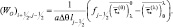 (2.165)
(2.165)
Помимо воздействия на вертикальные движения, трение о земную поверхность оказывает свое действие на вектор горизонтального ветра. Сила трения в уравнениях горизонтального движения определяется на двух уровнях: уровне моря и следующем счетном уровне. Как известно, сила поверхностного трения входит в уравнения движения в виде:
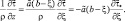 (2.166)
(2.166)
Из оценок модели Экмана следует, что приблизительно:
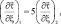 а
а 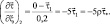
Тогда 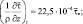
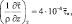 (2.167)
(2.167)
где  определяется по формулам (2.163).
определяется по формулам (2.163).
Полученные дополнительные слагаемые добавляются в правые части уравнений (2.158).
В экспериментах с орографией и трениям предполагалось, что коэффициент сопротивления СD на суше зависит от высоты гор следующим образом:
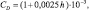 (2.168)
(2.168)
где h – высота горы в метрах.
Над океаном используются эмпирические соотношения работы [172]:
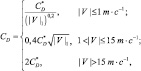 (2.169)
(2.169)
где