
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
3.1.3. Модель пограничного слоя атмосферы с незакрепленной верхней границей воздушной массы
В атмосфере часто наблюдаются инверсионные ситуации, когда более теплая воздушная масса находится выше холодной. Эти воздушные массы отделяются свободной поверхностью H(x, y, t), которая является искомой величиной. При этом можно предположить, что высота пограничного слоя атмосферы совпадает с нижней границей инверсии.
В отличие от постановки задачи пограничного слоя, где обычно верхняя граница имеет фиксированную высоту, в этом случае функция H(x, y, t) является одной из искомых характеристик. Поэтому, использование такой модели требует преобразования системы уравнений гидротермодинамики (3.17)–(3.23) таким образом, чтобы в ходе решения задачи, наряду с другими метеоэлементами, определить функцию H(x, y, t) и одновременно учитывать структуру рельефа подстилающей поверхности.
В настоящее время известен ряд способов определения высоты пограничного слоя атмосферы в зависимости от приземных турбулентных характеристик, и параметров фонового течения, основанных на формуле Дирдорфа [234], с величинами приземных потоков тепла и количества движения. Особенно важно описание физических процессов, происходящих вблизи верхней границы пограничного слоя. В данном случае высота H(x, y, t) представляет собой уровень, где возмущения метеорологических элементов затухают. Значение функции H(x, y, t) зависит от гидрометеорологических процессов всего пограничного слоя, и поэтому, чем богаче модель физически, тем более правильно можно охарактеризовать эту высоту.
Рассмотрим систему уравнений гидротермодинамики (3.1)–(3.23) при следующих начальных и краевых условиях:
u′ = 0; v′ = 0; θ′ = 0; q′ = 0; H(x, y) = H0(x, y) при t = 0; (3.31)
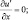
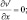
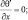
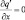 при x = ±X; (3.32)
при x = ±X; (3.32)
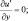
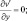
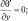
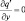 при y = ±Y; (3.33)
при y = ±Y; (3.33)
u′ = 0; v′ = 0; θ′ = αΔT; q′ = 0; π′ = 0; 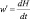 при z = H(x, y, t); (3.34)
при z = H(x, y, t); (3.34)
u = 0; v = 0; θ′ = f(x, y, t); 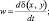
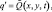 при z = δ(x, y), (3.35)
при z = δ(x, y), (3.35)
где ΔT = TТЕП – TХОЛ; H0(x, y) – начальная заданная высота слоя инверсии. Функции f,  предполагаются заданными.
предполагаются заданными.
В данном случае мы будем иметь задачу о пограничном слое атмосферы при движении воздушной массы над термически и орографически неоднородной поверхностью со свободной верхней границей воздушной массы, которая учитывается в краевых условиях (3.34).
Преобразуем (3.17)–(3.23) таким образом, чтобы получить уравнение для нахождения функции H(x, y, t).
С этой целью перейдем от переменных t, x, y, z к новым независимым переменным x′ = x; y′ = y; t′ = t и определим вертикальную координату следующим образом [4, 52, 53, 106]:
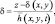
где 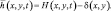 (3.36)
(3.36)
Функция δ(x, y) описывает рельеф подстилающей поверхности. Ордината z теперь зависимая переменная, определяемая, согласно (3.36), как
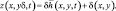 (3.37)
(3.37)
Переход от первоначальной системы координат t, x, y, z к новой t′, x′, y′, δ осуществляется с помощью следующих преобразований:
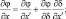
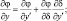
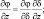 φ = (u, v, θ, q, π). (3.38)
φ = (u, v, θ, q, π). (3.38)
В новых переменных символ индивидуальной производной будет иметь вид:
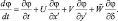 (3.39)
(3.39)
В (3.39) фигурирует неизвестная функция 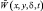 (аналог вертикальной скорости), которая связана с W с соотношением:
(аналог вертикальной скорости), которая связана с W с соотношением:
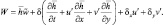 (3.40)
(3.40)
В новой системе координат уравнения гидротермодинамики (3.17)–(3.23), описывающие локальные атмосферные движения, примут следующий вид:
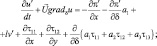 (3.41)
(3.41)
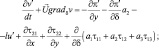 (3.42)
(3.42)
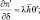 (3.43)
(3.43)
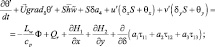 (3.44)
(3.44)
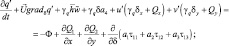 (3.45)
(3.45)
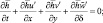 (3.46)
(3.46)
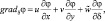 φ = (u, v, θ′, q′),
φ = (u, v, θ′, q′),
где θx, θy, Qx, Qy – горизонтальные градиенты фоновой потенциальной температуры и влажности.
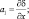
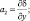
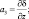
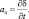 (3.47)
(3.47)
Начальные и краевые условия (3.31)–(3.35) преобразуются соответственно в следующие:
u′ = 0; v′ = 0; θ′ = 0; q′ = 0; H(x, y) = H0(x, y) при t = 0; (3.48)
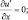
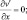
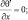
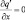 при x = ±X; (3.49)
при x = ±X; (3.49)
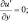
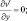
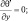
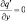 при y = ±Y; (3.50)
при y = ±Y; (3.50)
u′ = 0; v′ = 0;  θ′ = αΔT; q′ = 0; π′ = 0; при δ = 1; (3.51)
θ′ = αΔT; q′ = 0; π′ = 0; при δ = 1; (3.51)
u = 0; v = 0; θ′ = f(x, y, t); 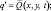
 при δ = 0. (3.52)
при δ = 0. (3.52)
Условие (3.52) имеет место в том случае, когда система уравнений пограничного слоя атмосферы решается без учета квазиоднородного приземного слоя. С подключением уравнений приземного слоя вид краевых условий (3.52) несколько изменяется, что будет рассмотрено несколько позже.
Прежде чем перейти к решению задачи (3.31)–(3.32), целесообразно осуществить некоторое преобразование уравнений. Проинтегрируем уравнение неразрывности (3.46) по δ. Учитывая условия для  при δ = 1, получим:
при δ = 1, получим:
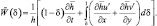 (3.53)
(3.53)
При δ = 0 из краевого условия (3.52) и уравнения (3.53) следует:
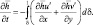 (3.54)
(3.54)
В дальнейшем, наряду с уравнением (3.46), будем пользоваться уравнением неразрывности в форме (3.54). Подставляя (3.54) в (3.53), получим диагностическое уравнение для определения 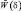 – аналога для вертикальной скорости:
– аналога для вертикальной скорости:
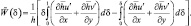 (3.55)
(3.55)