
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
3.2.5. Иллюстративный пример
Рассмотрим результаты расчетов, полученных с помощью разработанной численной модели распространения примеси для следующей модельной ситуации. Пусть в области размером Х = Y = 70 км, H = 1700 м имеется источник пассивной примеси на высоте Hs = 250 м при Х = Y = 0, ∆х = ∆у = 4 км, ∆z = 50 м при z ≤ 200 м, Δz = 200 м при z > 200 м, kH = 200 м2/с, U = 5 м/с, v = w = 0. Интегрирование по времени проводилось на интервале, равном 24 ч. На рис. 10 приведены результаты расчета проинтегрированной поперек ветра средней концентрации Су, нормированной на величину Q/HU, где Q – мощность выброса источника. Распределение примеси соответствует установившемуся состоянию. Из анализа рисунка видно, что вблизи источника ось факела (т.е. линия максимальных концентрации) опускается вниз и достигает подстилающей поверхности. Это явление подтверждается данным многочисленных наблюдений.
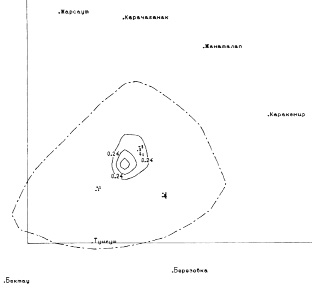
Рис. 10. Изолинии концентрации SO2 в долях ПДК на высоте 50 м при конвективных условиях. Скорость поперечного ветра 3 м/с
С целью экономичности расчетов нами были использованы некоторые упрощения, связанные с определением необходимых для моделирования рассеяния вредных примесей метеоэлементов.
В частности, классификация атмосферной устойчивости от которой зависит интенсивность турбулентной диффузии, приводится с использованием стандартной методики Раксвилла-Гиффорда.
По этой методике в зависимости от скорости ветра, времени суток, солнечной инсоляции и градиента температуры в пограничном слое атмосферы (ПСА) определяются шесть классов устойчивости (А, В, С, D, F), начиная от А (наибольшая неустойчивость) и вплоть до F (наибольшая устойчивость).
Скорость ветра, как уже отмечалось, имеет горизонтальную однородность и задавалось с использованием простейшей Экмановской модели пограничного слоя. Интенсивность турбулентной диффузии по высоте ПСА задавалось с использованием параметра устойчивости в приземном слое атмосферы L и динамической скорости как и в [22]. Определение L и u проводилось согласно подходу, где конкретные значения этих параметров выбрались (для каждого класса устойчивости) в зависимости от известной скорости ветра вблизи земной поверхности и параметра шероховатости подстилающей поверхности z0.
Сила ветра в ПСА определялась по степенному закону:
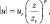
где p – показатель степени, зависящий от z0 и класса устойчивости; ur – известное значение приземного ветра на высоте zr.
Угол поворота вектора скорости в ПСА (по модели Экмана) задается выражением:
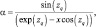
где 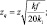 k – параметр Кармана 45; f – параметр Кориолисса; k1 – коэффициент вертикального обмена на высоте
k – параметр Кармана 45; f – параметр Кориолисса; k1 – коэффициент вертикального обмена на высоте  .
.
Кроме того, в модели также были использованы следующие внешние по отношению к ПСА метеопараметры: h – высота приземного слоя атмосферы; zn – высота ПСА; αg – направление геострафического ветра в выбранной системе координат. Используемые при расчетах значения этих метеопараметров и параметры шероховатости представлены в табл. 36.
Таблица 36
Значение внешних параметров
|
Тип метеоситуации |
H |
z0 |
zn |
αg |
zr |
ur |
|
Конвективные условия |
10 |
0,1 |
600 |
10° |
8 |
3 |
|
Устойчивые условия |
50 |
0,1 |
1500 |
–30° |
8 |
2 |
4. Математическое моделирование переноса вредных примесей в приземном слое атмосферы
При моделировании атмосферной циркуляции и распространении примесей в приземном слое атмосферы получены системы уравнений квазиоднородного приземного слоя, потока тепла и влаги в почву, а также проведено замыкание системы уравнений гидротермодинамики относительно оператора турбулентного обмена. Выведены уравнения блочной модели переноса вредных примесей в приземном слое атмосферы и описаны взаимодействия между блоками, а также разработаны численные схемы блочной модели переноса вредных примесей в бароклинной атмосфере. Проведены численные расчеты переноса вредных веществ в приземном слое атмосферы с учетом влияния подстилающей поверхности.