Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

4.1.2. Поток тепла и влаги в почву

Во многих численных моделях динамики атмосферы для нахождения температуры почвы используется уравнение теплового баланса. Теплофизические характеристики почвы разнообразны, в результате чего даже в небольших расстояниях температуры над различными типами почвы могут резко различаться и тем самым влиять на динамику атмосферы в нижних слоях. Кроме того, тепловой и влажностные режимы в системе почва – воздух из-за взаимной связи между
собой воздействуют на формирование и развитие растений и тем самым влияют на окружающую среду.

В настоящее время решение такой комплексной задачи удается получить благодаря ряду упрощений. Тем не менее, имеется несколько физических моделей, которые качественно правильно отражают ход естественных процессов [381, 382]. Ясно, что тепловой режим в почве может быть наиболее полном описан на основе совместного рассмотрения процессов молекулярной теплопроводности почве и турбулентной теплопроводности в области приземного слоя атмосферы. В рамках одномерной модели пограничного слоя эти работы использовались в работах [381, 382].

Теперь, как и в [381], рассмотрим процессы теплообмена в почве с учетом термодинамического состояния почвенной среды совместно с пространственной моделью пограничного слоя атмосферы. Исходным для нахождения температуры на поверхности земли является уравнение теплового баланса (4.11). Для определения тепловых и влажностных характеристик почвы рассмотрим следующее уравнение:

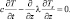(4.24)

Здесь С – теплоемкость почвы, задаваемая по формуле:

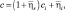(4.25)

где  – объемное влагосодержание; а  – насыщающая влага или пористость почвы; ci – теплоемкость сухого грунта для соответствующего почвенного типа i.

В уравнении (4.25) теплоемкость воздуха не учитывается из-за ее малости. Коэффициент теплопроводности λ определяются с помощью следующих эмпирических формул, полученных из аппроксимации эмпирических данных [107]:

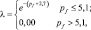(4.26)

где 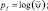 – потенциал влаги в почве.

Здесь, как и в модели квазиоднородного приземного слоя, однородность почвы по горизонтали предполагается только в пределах одной ячейки сеточной области.

Отметим, что потенциал влаги соответствует верхнему горизонту воды и представляет собой работу против капиллярных сил и силы сопротивления, затрачиваемую на выделение воды из почвы. Из анализа экспериментальных данных получено, что связь между коэффициентом теплопроводности и потенциалом влаги слабо зависит от типа почвы.

Распределение количества влаги в почве η определим из уравнения:

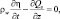(4.27)

где 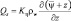(4.28)

или 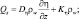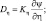(4.29)

Qs – поток влаги в почве; Kη – гидравлическая проводимость; ρw – плотность воды; z – вертикальная координата, определяемая как и в атмосфере; Dη – коэффициент диффузии.

Следуя [381] определим переменные Kη, , Dη с помощью формул:

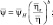(4.30)

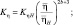(4.31)

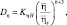(4.32)

где индексом «Н» отмечены значения соответствующих функции в условиях насыщения.

Одним из основных искомых параметров является относительная влажность или потенциал поверхности влаги. Связь между ними при равновесии представим в виде:

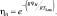(4.33)

Тогда удельная влажность на поверхности земли равна:

q3em = η0qH, (4.34)

а qH находится из формулы Магнуса (4.20).

Изменение влажности почвы влечет за собой изменение баланса радиации на поверхности земли из-за изменения альбедо подстилающей поверхности. С увеличением влажности альбедо уменьшается. Альбедо As на поверхности почвы в первом приближении определим с помощью следующих эмпирических формул [101]:

– для чернозема:

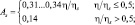(4.35)

– для торфа:

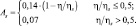
Общее альбедо подстилающей поверхности можно представить в виде:

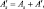(4.36)

где A′ учитывает зависимость зенитного угла солнца следующим образом:

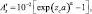(4.37)

zc – зенитный угол солнца; a = 0,0003286; α = 1,5. Теперь с учетом уравнения теплового баланса (4.11) необходимо согласовать поток влаги Qs, идущий из почвы к поверхности земли, и турбулентный поток влаги, поступающий из почвы в атмосферу Q1 = ρu*q*. Для этого достаточно потребовать, чтобы

Q1 = Qs. (4.38)

Замыкание системы уравнений гидротермодинамики относительно оператора турбулентного обмена производится согласно п. 3.1.4 раздела 3.

В силу этих обстоятельств модель атмосферных процессов и климата представим в системе нелинейных дифференциальных уравнений гидродинамики турбулентной атмосферы и диффузии примесей [4]:

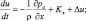
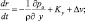
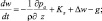(4.39)

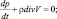
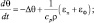
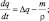
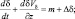
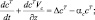
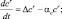pA = ρRT;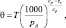

где t – время; u, v, w – компоненты скорости ветра вдоль декартовых осей x, y, z соответственно; pA – атмосферное давление; ρ – плотность воздуха; g – ускорение силы тяжести; Kx, Ky, Kz – компоненты силы Кориолиса 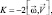(где ω – угловая скорость вращения Земли); T – температура; θ – потенциальная температура; cp, cv – удельные теплоемкости при постоянном давлении и объеме соответственно; q – удельная влажность воздуха; δ – водность воздуха; cT – концентрация твердых примесей; Vδ – скорость опускание жидкой влаги; Vc – скорость опускание твердых примесей; cv – концентрация газообразных примесей; m – скорость конденсации (испарения) влаги; επ – лучистый приток тепла; εΦ = ΦT – фазовый приток тепла (где Ф – удельная теплота парообразования); R – удельная газовая постоянная сухого воздуха;  – коэффициент, определяющий изменения концентрации за счет химических превращений примесей.

Скорость фазовых переходов влаги m в случае термодинамического процесса в воздухе, насыщенном водяным паром, может быть определена по формуле:

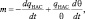(4.40)

где 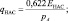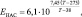(4.41)

где qHAC – удельная влажность насыщения; EHAC – упругость насыщения водяного пара.

Лучистый приток тепла επ представляет собой дивергенцию результирующего потока Ф:

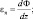
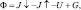(4.42)

где 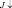,  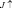– нисходящий и восходящий потоки коротковолновой радиации; G, U – нисходящий и восходящий потоки длинноволновой радиации, которые описываются интегродифференциальными уравнениями переноса излучения [4]. Скорость опускания тяжелой сохраняющейся примеси Vc и водяных капель Vk радиусом 10–5 – 5∙10–3 может быть определена по известной формуле Стокса для сферических частиц [5]:

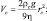(4.43)

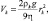(4.44)

где ρc, ρk – плотности примеси, капли; rc, rk – радиусы частиц примеси, капли; g – ускорение силы тяжести; η – коэффициент молекулярной вязкости воздуха.

Для крупных частиц примеси в формулу (4.43) вводят поправочный коэффициент , где 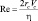[7]. А для капель воды радиусом 0,5 мм и более применяют эмпирические зависимости скорости падения капли от эквивалентного радиуса капли (радиуса шара, объем которого равен объему деформированной капли) [5].

Для расчета скорости опускания влаги в атмосфере Vδ вводят понятие средневзвешенной (по массе) скорости падения облачных капель:

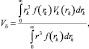(4.45)

где f(rk) – функция распределения капель по размерам.

В уравнениях (4.39) используется операторы:

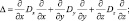
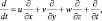
где Dx, Dy, Dz – коэффициенты турбулентной диффузии по осям x, y, z.

Связь тепловых режимов атмосферы и деятельного слоя почвы осуществляется с помощью уравнения теплового баланса земной поверхности (уравнения притока тепла, записанного для очень тонкого слоя) [5]:

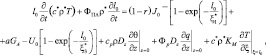(4.46)

где Т – температура слоя почвы; l0 – толщина слоя; с* – удельная теплоемкость почвы; ρ* – плотность почвы; KM – коэффициент молекулярной температуропроводности; ΦΠΛ – удельная теплота плавления; r – альбедо поверхности почвы; a – коэффициент поглощения (излучения) почвы; J0↓ – коротковолновая радиация, приходящая к поверхности почвы; GA – противоизлучения атмосферы; U0 – излучение земной поверхности; 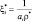(i = 1, 2, 3) – глубины, на которых потоки радиации J0↓, GA, U0 убывают в «е» раз по сравнению с соответствующими потоками при ξ = 0; ai – коэффициенты поглощения слоя почвы для J0↓, GA, U0.

Процесс распределения тепла в глубь почвы путем молекулярной теплопроводности описывается уравнением теплопроводности почвы (или уравнением притока тепла), которое имеет вид [5]:

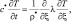(4.47)

где с* – удельная теплоемкость почвы; ρ* – плотность почвы; λ – коэффициент теплопроводности почвы; ξ – глубина от поверхности почвы.

Уравнение (4.47) справедливо для сухих или насыщенных влагой почв. В ненасыщенной почве необходимо учитывать взаимосвязанный характер переноса влаги и тепла [6]:

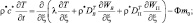
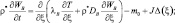(4.48)

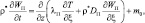
где WB, WП – удельная влажность жидкости и пара соответственно; λB, λП – коэффициенты термовлагопроводности; DB, DП – коэффициенты диффузии; 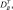 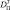– коэффициенты влаготермопроводности; m0 – объемный источник, отражающие взаимные фазовые переходы жидкости и пара; J – интенсивность осадков; Δ(ξ) – дельта-функция.

В большинстве реальных случаев для почвы выполняется соотношения [6]:

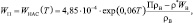(4.49)

где П – пористость почвы; ρВ – плотность воды.

Связь режимов влаги атмосферы и почвы осуществляется с помощью уравнения баланса влаги земной поверхности:

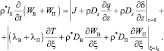(4.50)

Интенсивность осадков связана с микрофизическим строением облаков и их вертикальной мощностью Δz. Получена эмпирическая зависимость J от Δz [5].

Для толщины облака Δz, в свою очередь существуют эмпирические взаимосвязи с водностью облака δ и температурой на нижней границе TНГ [5].

Система уравнений (4.39)–(4.50) описывает метеорологические явления всех масштабов, в том числе и локального. Однако, в общем случае, численные методы решения связанных с ней задач оказываются чрезвычайно громоздкими и неприемлемыми для современных ЭВМ.

Для перехода к блочной модели проще всего воспользоваться в теории [1] операцией осреднения переменных и уравнений по пространственным координатам для выделенных блоков модели и далее описать взаимодействия каждого блока с соседними.