Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

4.2. Вывод уравнений блочной модели переноса вредных примесей в приземном слое атмосферы и описание взаимодействий между блоками

Для эффективного исследования сложного объекта математическими методами требуется иметь комплекс моделей различных уровней и детализации. Это взаимодействие различное (расшифровка, детальная интерпретация в подобных моделях, решение принятых с помощью ориентированных моделей верхнего уровня и эксперименты с моделями нижнего уровня с целью уточнения параметров моделей верхнего уровня и т.д.). Когда требуется поставить массовые машинные эксперименты с готовой моделью с целью формирования необходимой статистики для решения поставленной задачи, громоздкость, детальность модели не позволяют это сделать при имеющихся вычислительных средствах. Тогда желательно построить менее подробную и точную, но существенно более операбельную модель с помощью имеющейся и уже с ней проводить массовые эксперименты. Доказательство этого существующие модели водной и воздушной среды, которые были использованы в разделах 2 и 3. Они являются развитием известных в механике и физике гидродинамических моделей, дополненных моделями термодинамических и иных явлений, позволяющие вести весьма точные расчеты характеристик гидродинамических, метеорологических, климатических
явлений при полностью заданных исходных данных (входах). Эти характеристики необходимы для многих моделей природной среды разных временных и пространственных масштабов и далеко не всегда могут быть получены из несистематизированных наблюдений, какими располагает наука: систематизированные в должной мере наблюдения таких распределенных объектов чрезвычайно дорогостоящи и далеко не всегда осуществимы имеющейся аппаратурой. Дело осложняется тем, что входные факторы (метеорологические условия) имеет случайный характер, и получение устойчивых характеристик может быть обеспечено лишь достаточно большими статистическими выборами, что весьма трудно реализовать путем, как наблюдений, так и расчетов на громоздких моделях. Вполне разумно в такой ситуации переходить от распределенных моделей к приближенным блочным моделям, поскольку основным фактором, определяющим большие объемы вычислений является распределенность объекта. Рассмотрим процедуру построения блочной модели локального климата, ее взаимодействия и принципы разбиения области моделирования. Понятие локального климата охватывает процессы и явления, имеющиеся горизонтальные масштабы от нескольких сотен метров до нескольких сотен километров с характерным масштабом по времени от нескольких часов до 3–4 суток. Процессы типа образования «острова тепла» над городом или крупным центром производства энергии, где действует одновременно много факторов одного порядка. Вертикальный масштаб таких явлений от 1 до 2 км, в некоторых случаях до 10 км (кучевая облачность). Поэтому вполне естественно выделить пространственные области моделируемой области как цилиндрические и разделить на ячейки.

При вертикальном делении, прежде всего, выделяем пограничный слой (1,5–2 км), в котором вертикальные элементы метеоэлементов намного больше соответствующих значений в свободной атмосфере (2–10 км) [2]. Внутри пограничного слоя его нижняя часть, приземный слой (50–100 м), обладает особым свойством – постоянством с высотой турбулентных потоков количества движения, тепла, водяного пара, коллоидных примесей. Толщина приземного и пограничного слоя меняется в зависимости от скорости ветра, шероховатости земной поверхности и устойчивости стратификации атмосферы [3].

Слой почвы можно разделить на три части: поверхность почвы, являющейся границей двух сред; слой суточных колебаний температуры (~1 м); слой годовых колебаний температуры (~10 м). Толщина выделенных в почве слоев зависит от свойств почвы [2].

Выделенные слои внутри каждой ячейки образует блоки. Между ними происходит горизонтальный и вертикальный обмен веществом и энергией. Рассматриваются средние значения переменных внутри каждого блока, и с их помощью описываются основные метеорологические процессы, формирующие мезоклимат в ячейке, и взаимодействие с соседними по горизонтали ячейками.

Неизвестных функций в уравнениях гидродинамики турбулентной атмосферы и диффузии примесей (4.39)–(4.50) параграфа 4,1 представим в виде суммы:

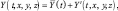
где 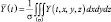 – среднее значение функции в камере (σ – объем
блока), а Y′(t, x, y, z) – отклонение от среднего внутри блока. И затем усредним
уравнения гидродинамики турбулентной атмосферы и диффузии примесей [4] по объему блока σ, используя свойства операции осреднения [1]:

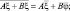
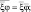
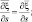
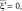
где ξ, φ – функции независимых переменных x, y, z, t; A, B – постоянные; s – любая из этих независимых переменных.

Покажем на примере первого уравнения системы гидродинамики турбулентной атмосферы и диффузии примесей [4] производимые действия:

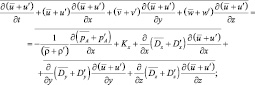
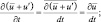
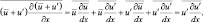
Аналогично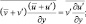

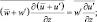
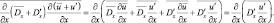
Аналогично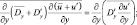

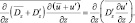
Пренебрегая пульсациями плотности (ρ′ = 0), получим:

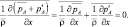
В данной модели плотность воздуха ρ считается меняющейся только по высоте и определяется как средняя интегральная плотность слоя Δz по формуле:

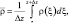
где ρ(ξ) задается таблично по многолетним средним данным значений давления и плотности на различных высотах [2]. Обозначая

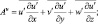
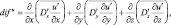
получим следующий вид первого уравнения системы (4.47)–(4.58):

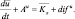
Поступая подобным образом с остальными уравнениями системы (4.39)–(4.50), придем к следующей системе уравнений для средних значений неизвестных функций в блоке модели:

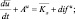
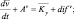
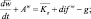
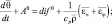
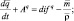
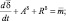(4.51)

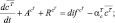
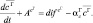
Здесь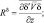

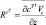
Члены AY и difY, где Y = (u, v, w, θ, q, δ, cT, cΓ), обусловливают адвективные (конвективные) и диффузионные изменения средних значений неизвестных функции блока. Эти изменения возникают, очевидно, в результате взаимодействия рассматриваемого блока с соседними. Для блока в почве в результате осреднения аналогичным способом получаем уравнения (без учета термического влагопереноса):

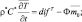
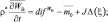(4.52)

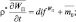
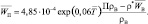
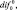
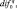
Уравнения теплового баланса земной поверхности нет необходимости осреднять, так как оно записано для слоя конечной длины l0. Обозначим три первых члена правой части через επ0, а члены обуславливающий диффузионные изменения температуры поверхности, через 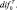Тогда уравнения теплового баланса земной поверхности примет вид:

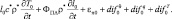(4.53)

Уравнение баланса влаги земной поверхности также остается без изменения и лишь в новых обозначениях примет вид (без учета термического влагопереноса):

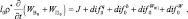(4.54)

Система уравнений (4.51)–(4.54) описывает изменение во времени средних значений метеоэлементов в каждой из выбранных блоков. Определив члены, отражающие взаимодействие между блоками (AY, difY, Rδ, 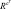), получим основные уравнения предлагаемой блочной модели.

Изменение субстанции Y в камере непосредственно определяется разностью потоков входящего QU и исходящего Q (притоком):

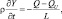
где L – длина камеры по нормали к площадке.

Для конвективного и адвективного притоков AY субстанции Y к камере легко получить:

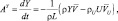(4.55)

где Y = (θ, q, δ, cT, cΓ, u, v, w); 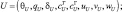 – средняя скорость перемещения субстанции.

Для описания диффузионных изменений difY используется следующий метод [10].

Рассматривается диффузия (молекулярная или турбулентная) между соседними камерами, в каждой из которых в начальный момент времени субстанции Y распределена равномерно (Y = U). Камеры считаются изолированными от окружающего пространства.

Процесс изменения Y описывается одномерным уравнением диффузии:

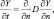t ∈ [0, T], n ∈ [0, LU + LY], (4.56)

и вместе с граничными и начальными условиями:

Y(0, t) = U; Y(LU + LY, t) = Y;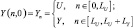

получается первая краевая задача математической физики.

Решение этой задачи дает распределение Y(n, t) по оси n по времени t. Средние значения субстанции Y в каждый момент времени t найдем интегральным осреднением Рейнольдса (4.54). Очевидно, что скорость изменения средних , пропорциональна их разности. Следовательно, можно записать систему обыкновенных дифференциальных уравнений относительно и  вида:

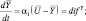
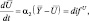(4.57)

где α1, α2 – коэффициенты, характеризующие интенсивность процесса диффузии, которые подлежат определению. Они являются функциями коэффициента диффузии и размеров рассматриваемых объемов (в модели-камер) вдоль нормали к площадке, через которую происходит диффузия.

Имеется еще один вид переноса вещества – опускание под действием силы тяжести тяжелых частиц: капель воды, пыли и т.п. Изменение водности и концентрации тяжелых примесей за счет опускания может быть описано уравнениями типа (4.54):

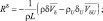(4.58)

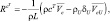(4.59)

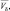
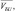
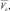
где  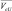– средние скорости опускания соответствующих субстанции в рассматриваемой и соседних камерах; ρU, δU – плотность и водность соседней по вертикали камере, из которой происходит опускание.

Коротковолновые и длинноволновые потоки радиации, проходящие через k-й слой атмосферы, описываются по элементарной схеме, предложенных для упрощенных расчетов [390]. Атмосфера представляется в виде N однородных слоев. Каждый k-й слой характеризуется коэффициентами отражения, поглощения и пропускания коротковолновой радиации rk, ak, hk, коэффициентами пропускания и излучения (поглощения) длинноволновой радиации pk, ek, причем:

rk + ak + hk =1, pk + ek = 1. (4.60)

Количество слоев N совпадает с количеством воздушных камер одной ячейки. При необходимости можно выделить дополнительные слои внутри камеры.

Нисходящий и восходящий коротковолновые потоки 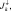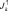описываются уравнениями:

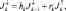
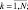
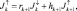
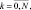(4.61)

где 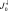 – поток солнечной радиации на верхней границе атмосферы (считается известным);  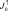– поток, уходящей за пределы атмосферы радиации; rN+1 = rП – альбедо подстилающей поверхности; hN+1 = 0.

Для потока длинноволновой радиации, с учетом того, что каждый слой атмосферы излучает тепловую энергию, получаются уравнения:

Gk = pkGk–1 + Bkek,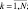

Uk = pk+1Uk+1 + Bk+1ek+1, 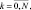(4.62)

где G0 = 0; UN+1 = GN, Bk – интегральная интенсивность излучения абсолютно черного тела:

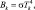(4.63)

где σ – постоянная Стефана-Больцмана.

В данной схеме переноса лучистой энергии, коэффициенты rk, ak, hk, pk, ek в дальнейшем необходимо определить через компоненты атмосферы, изменяющие потоки радиации путем излучения, поглощения и рассеяния.