
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ
Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,
5.4. Модель расчета концентрации от нестационарного непрерывного источника при аварийном выбросе
В работе [22] предлагается численный алгоритм решения задачи турбулентной диффузии примеси от нестационарного приподнятого точечного источника в пограничном слое атмосферы и анализ влияния изменения мощности выброса на результирующие характеристики загрязнения [416].
Нестационарная задача диффузии, представленная в виде комбинации гауссовской аппроксимации – для расчета диффузии в поперечном по отношению к переносу направлении, турбулентной диффузии по вертикали, адвективного переноса по оси факела и формируется следующим образом:
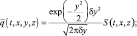 (5.23)
(5.23)
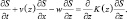 (5.24)
(5.24)
При граничных условиях:
 (5.25)
(5.25)
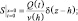 (5.26)
(5.26)
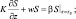 (5.27)
(5.27)
 (5.28)
(5.28)
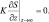 (5.29)
(5.29)
Здесь s и q – «плоская» и объемная концентрация соответственно.
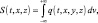 (5.30)
(5.30)
где Q(t) – мощность выброса; h – высота источника; w – скорость гравитационного оседания примеси; β – коэффициент захвата примеси на подстилающей поверхности (0 ≤ β < ∞); v(z) и K(z) – вертикальные проекции скорости ветра и коэффициента турбулентности в пограничном слое; σy – дисперсия факела в поперечном ветру направлении y; t – время от начала работы источника; х – расстояние от источника; δ(z – h)– дельта функции Дирака.
Задача в постановке (5.23)–(5.29) имеет следующее аналитическое решение при постоянных коэффициентах v = v(h) и k = k(h):
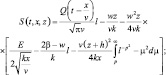 (5.31)
(5.31)
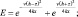 (5.32)
(5.32)
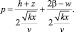 (5.33)
(5.33)
Такое решение (5.31) может удовлетворительно описать распространение сероводорода при аварийных выбросах из порывов трубопроводов в условиях эксплуатации КНГКМ.
Для газообразной примеси при w = 0 и β = 0 задача диффузии сведется к следующему:
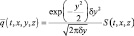
при тех же граничных условиях, кроме условия (5.27):
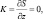 (5.34)
(5.34)
где 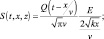 (5.35)
(5.35)
Е из (5.32).
Если к тому же предположить, что рассматривается задача распространения загрязнения от одного точечного источника, то есть без учета наложения полей загрязнения (y = 0), то задача еще несколько упростится, а именно:
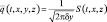
при тех же граничных условиях, где S(t, x, z) и Е определяются соответственно по (5.31) и (5.32).
В пограничном слое перенос примеси существенным образом зависит от вертикальной неоднородности метеорологических элементов v(z) и k(z). Поэтому получение разумных количественных результатов обеспечивается только путем численного решения задачи диффузии с учетом реальных v(z) и k(z).
Для определения параметров v(z) и k(z) можно степенную модель, в которой полагается:
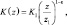
где 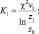 χ = 0,4 – постоянная Кармана; z – высота определения концентрации; v1 – скорость на высоте 1 м, определяемая по формуле:
χ = 0,4 – постоянная Кармана; z – высота определения концентрации; v1 – скорость на высоте 1 м, определяемая по формуле:
v(z) = v(10)(z/10)p,
где p определяется по таблицам, в зависимости от класса устойчивости и параметра шероховатости; z1 – высота замера; ε – определяется по таблице.
Стандартные отклонения распределения концентраций по оси y, то есть дисперсию факела, для расстояний от источника выбросы менее 10 км, можно рассчитывать по формулам, предложенным Пэскуила-Гиффорда [15].
Комплексная модель промышленных источников для расчета кривых σy использует следующие эмпирические выражения:
σy = 465,1163∙tg(m), m = 0,017453∙(c – d∙lnx),
где c, d – определяются по таблицам при классах устойчивости Пэскуила.
Идентификация метеопараметров в моделях турбулентной диффузии загрязняющих веществ в атмосфере. Численное и аналитическое решение уравнений турбулентной диффузии в моделях распространения загрязнения в атмосфере требуют определения зависимости основных метеопараметров от высоты. В случае отсутствия возможности измерений с достаточным разрешением по времени и по пространству возникает необходимость ее аппроксимации.
В слое трения (приземной слой), толщина которого зависит от температурной стратификации, происходит изменение скорости и направления с высотой. В этом слое направление ветра с высотой испытывает поворот вправо, а модуль возрастает как логарифм высоты:
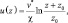
где χ – постоянная Кармана; v* – динамическая вязкость; z0 – коэффициент шероховатости.
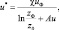
где zΦ – высота измерения скорости ветра (высота флюгера); Au – коэффициент, зависящий от класса устойчивости атмосферы.
По экспериментальным оценкам средняя толщина слоя перемешивания составляет для устойчивости стратификации (инверсия) 50 м, для безразличной (изотермия) ≈ 70 м, для неустойчивой (развитая конвенция) ≈ 100 м [17].
Как показывают наблюдения, существенное значение имеет вид распределения температуры по высоте, для определения которого разработано множество методов, доступных измерению у земли (скорость ветра, солнечная инсоляция и др.). Наиболее допустимыми являются метод Пэскуила [17].
Эти методы дают количественное значение градиента температуры в рассматриваемом слое (табл. 41).
Существенно улучшает модели турбулентной диффузии также знание вертикального распределения коэффициента турбулентной диффузии Kz [18]. Определению Kz на высоте 1 м по данным градиентных наблюдений посвящен ряд работ [17, 18]. При нейтральной стратификации все методы сводятся к одному и тому же соотношению:
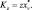
Однако, при неравновесных состояниях для расчета используется специальная безразмерная функция:
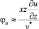
с учетом 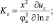
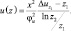
Зависимость φu от динамического (Rf) и градиентного (Ri) числа Ричардсона при неустойчивой стратификации имеет следующий вид:
φu = (1 – σRf)–1/4; φu = (1 – σ′Ri)–1/4,
где σ и σ′ находятся в пределах от 12 до 18 и от 11 до 17 соответственно.
Таблица 41
Характеристики классов устойчивости и значения параметров,
полученных по экспериментальным зависимостям
|
№ |
Качественная характеристика класса устойчивости |
Описание погоды |
Обозначение по Пэскуиллу |
u |
γ, C0/100M |
Б |
μ |
|
1. |
Очень неустойчивое состояние развития конвекции |
очень солнечная, летняя, тихая |
А |
1 |
–1,9 |
0,04 |
|
|
2. |
Неустойчивая, умеренная конвекция |
солнечно, тепло |
В |
2 |
–1,9...–1,7 |
–0,03 |
|
|
3. |
Легкая неустойчивость, слабая конвекция |
переменная облачность |
С |
5 |
–1,0...–1,5 |
–0,09...–0,002 |
–50 |
|
4. |
Безразличное, нейтральное |
облачно |
Д |
5 |
–1,4...–0,5 |
0 |
|
|
5. |
Слегка устойчивая слабая инверсия |
переменная облачность ночью |
Е |
3 |
–0,4...1,5 |
0,002...0,004 |
50 |
|
6. |
Устойчивое состояние, умеренная инверсия |
ясная ночь |
F |
2 |
1,6...4,0 |
+0,01...+0,04 |
100 |
|
7. |
Очень устойчиво, сильная инверсия |
то же |
G |
1 |
40 |
≥ 0,05 |
100 |
А для высоты 1 м:
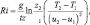
где T1, T2 – температура воздуха на уровне 1 и 2 м или полуэмпирическое:
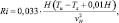
где Tu – температура на высоте Н от поверхности; Tz – температура на высоте выброса z; Н = 300 м или верхняя граница инверсии [17].
В условиях несложного рельефа и отсутствия застроек горизонтальные составляющие коэффициента турбулентности определяются соотношением:
Kxy = aKz,
где a = 2 для устойчивой атмосферы, a = 1 для безразличной, a = 0,5 – для неустойчивой.
Таким образом, на основе стандартных метеонаблюдений можно определить вертикальное распределение скорости ветра, температуры и коэффициента турбулентности, детальное знание которых существенно улучшает модели распространения примесей в атмосфере.
Итак, изложены три возможных подхода к решению задачи динамического прогноза.
Анализ возможности использования методов численного моделирования показывает, что этот подход имеет наиболее развитую теоретическую базу и в принципе позволяет учитывать практически все основные факторы, влияющие на процессы рассеяния СДЯВ. В настоящее время этот метод реализован на ЭВМ ЕС-1045 [13], которая относится к классу техники с наиболее мощными вычислительными возможностями. Уже в процессе реализации стало очевидно, что даже этих возможностей недостаточно для реализации трехмерного варианта метода. Реализована была двухмерная модель, не учитывающая процессы рассеяния в плоскости вертикальной земной поверхности. Кроме того, накладывались достаточно жесткие ограничения на число узлов пространственной координатной сетки, в которых считаются концентрации. Только при оперировании с небольшими числами узлов, порядка 20–30, время счета для прогнозирования оставалось в разумных пределах (неравенство (1)). Для прогнозирования в достаточно больших областях, например: 20×30 км на КНГКМ, расстояние между узлами получается очень большим. Все это приводит к вычислительной неустойчивости данной реализации метода, что и было подтверждено при проведении численных экспериментов на ЭВМ. Результаты, которые получились при этом, не выдерживали никакой критики даже при анализе на основе самой элементарной логики рассуждений. Например, при достижении границы рассматриваемой области наблюдался эффект отражения фронта и распространения загрязнителя в обратном направлении. Итак, подытоживая анализ методов численного моделирования, можно констатировать несоответствие их условиям прогнозирования распространения сероводорода на КНГКМ. Мы как бы оказываемся зажатыми между двух требований: необходимая точность и ограничения на время решения. Одновременное их выполнение даже на быстродействующих ЭВМ в настоящее время нереально.
Далее, вторая и третья модели достаточно просты в реализации и во многом сходны в части использования эмпирических знаний о процессах распространения и диффузии. Детальный анализ показывает, что комбинированная модель является наиболее общей, в частности, она использует более сложные характеристики метеоситуации. Последнее можно констатировать как положительный фактор – это повышает точность расчетов, так и отрицательный, ибо становится необходимым проведение сложных измерений метеопараметров. В частности, требуется определение высотных распределений температуры, скорости ветра.
По степени устойчивости атмосферы выделяются три группы:
– инверсия (устойчивая), для которой характерно слабое турбулентное перемешивание в пограничном слое атмосферы;
– изотермия (равновесная) с умеренным турбулентным перемешиванием;
– конвекция (неустойчивая), при которой отмечается цельное турбулентное перемешивание.
Степень устойчивости определяется на основе фактических и прогностических данных об облачности, измеряемой (в баллах) и скорости ветра для рассматриваемого времени суток (ночь, день, утро, вечер) с учетом наличие или отсутствие снежного покрова.
На рис. 25 представлены изолинии концентрации распространение сероводорода при аварийных выбросах из порывов трубопроводов в условиях эксплуатации КНГКМ на уровне Z = 2 м, расчетные показатели которых дают отклонения не более 15 % с данными экспедиционных натурных исследовании.
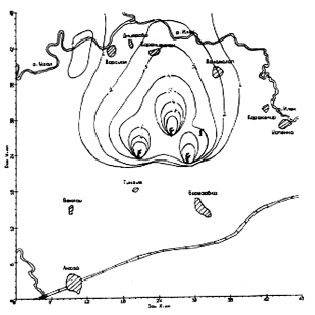
Рис. 25. Изолинии концентрации вредных веществ суммарного воздействия на уровне Z = 2 м
Итак, полуэмпирическая методика вполне применима для решения стоящих задач. Для определения условий и границ ее возможного использования, необходимо планирование и проведение серии экспериментов на объекте.
Анализ результатов работы в направлении создания системы прогноза динамики распространения опасного уровня концентрации сероводорода при аварийных выбросах приводит к следующим выводам:
1) ввиду многофазности потока в шлейфах и отсутствия достаточно адекватных математических моделей для таких потоков представляется проблематичным перекачиваемой смеси такой системы контроля шлейфов, в которой были бы обеспечены требуемая надежность, точность, оперативность обнаружения порывов;
2) акустические свойства трубопроводов (но не перекачиваемой смеси) могут быть положены в основу методики обнаружения порывов в шлейфах. В качестве приемников могут быть использованы датчики на основе пьезокирамики типа ЦТС-19. Полная стоимость разработки, поставки опытного образца системы контроля одного шлейфа составит ориентировочно 1850,0 тыс. тенге;
3) в системе контроля магистральных трубопроводов, в которых поток близок к однофазному, можно использовать как акустические характеристики труб, так и гидро-газо-динамические свойства потока;
4) на особо опасных направлениях может быть использована подсистема нейтрализации сероводородного облака;
5) методика решения задачи прогноза, разработанная в Главной геофизической обсерватории, является самой простой и удобной в использовании. Одновременно с этим она является и самой грубой. Но это будет вызывать не игнорирование опасных уровней загрязнения, а скорее некоторую перестраховку в расчетах, что в нашей ситуации вполне приемлемо. Преимуществом этой методики относительно комбинированной модели является и то, что она позволяет учитывать намерения метеоситуации в процессе рассеивания сероводородного облака;
6) значение метеорологических параметров, необходимые в методике, определяются по данным ближайшей репрезентативной метеостанции или специально организованного поста наблюдений. Скорость и направление ветра измеряются на высоте флюгера (10 м) с осреднением не менее 5 мин;
7) для КНГКМ рекомендуется методика решения прогнозной задачи;
8) адаптацию модели прогноза целесообразно провести в 2 этапа: первый этап – машинная адаптация и второй – на объектах.