Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

МОДЕЛЬНАЯ ОЦЕНКА ЭКОЛОГИЧЕСКОЙ ОБСТАНОВКИ КОМПАНЕНТОВ ПРИРОДНОЙ СРЕДЫ С УЧЕТОМ АТМОСФЕРНЫХ ПРОЦЕССОВ

Айдосов А. , Айдосов Г. А., Заурбеков Н. С.,

5.5. Моделирование аварийных выбросов из глубоких скважин с использованием струйной модели

Обычно, аварийная ситуация на нефтегазодобывающих месторождениях сопровождается выбросами в атмосферу холодного и горячего смеса сероводородных продуктов. При этом под воздействием повышенного давления внутри нефтегазоносного пласта формируется струя смеси или факел, в которых исходное вещество преобразуется в продукты сгорания. Затем они перемешаются с воздухом посредством механизма турбулентности. Таким образом, распространение аварийных выбросов в приземном слое воздуха можно свести к задаче рассеяние турбулентной струи.

Однако, область применения струйной модели существенно зависит от многих факторов, таких как характер подстилающей поверхности, высота источника над землей, поле ветра, турбулентность атмосферы и др.

Так, в условиях развитой турбулентности (высокие скорости ветра, конвективные процессы в пограничном слое атмосферы) предлагаемая модель дает
результаты, близкие к реальным, только на расстояниях порядка 100 м. И наоборот, когда турбулентность сильно подавлена (например, в условиях зимней инверсий) выброс может существовать в виде струи до гораздо больших расстояний (1–10 км). Наконец, от высоты источника зависят как интенсивность турбулентности, так и поле ветра, причем чем ниже источник, тем сильнее влияние поверхности (особенно, со сложной орографией) и, следовательно, тем меньше район применимости струйной модели, в которой, надо сказать, никак не учитываются ни орография, ни турбулентность. Масштабом для оценки области применимости этой модели может быть выбрано расстояние, где скорость диссипации турбулентной энергии в струе сравнивается с таковой для атмосферы.

Итак, пусть источником является круглое сопло радиусом r0, расположенное на земле, в точке x = z = 0. Скорость выбрасываемого газа v0 постоянна по его сечению. Газ горит, причем смешение его с воздухом и полное сгорание происходят на срезе сопла, так что дальше движутся разогретые до температуры Т0 продукты сгорания. Направление выброса α0 не обязательно вертикально. В приземном слое атмосферы предполагается вертикальная стратификация с градиентом температуры γ и постоянная скорость ветра w вдоль оси x0.

Теория рассеяния свободных турбулентных струй разработана достаточно подробно и широко применяется в гидродинамике. Нашу задачу будем решать, следуя монографии Е.В. Бруяцкого.

Турбулентная струя, согласно Г.Н. Абрамовичу, разделяется на две области: начальную и основную. На начальном участке имеется ядро постоянной скорости, температуры и концентрации выброса, радиус которого r уменьшается от r0 до нуля, а область смещения, наоборот, увеличивается до bH.

Исходными являются уравнения гидротермодинамики в системе координат, связанной с осью струи, относительно которой предполагается цилиндрическая симметрия в распределении зависимых величин. После некоторых преобразований эти уравнения интегрируются в плоскости, перпендикулярно оси струи [317]:

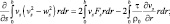(5.41)

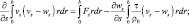(5.42)

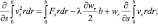(5.43)

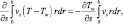(5.44)

где F – вектор массовых сил;  – сила турбулентного трения, действующая на единицу объема смеси; s – расстояние вдоль оси струи; r – расстояние от оси
в поперечном сечении; Tw – стратификация атмосферы; λ – коэффициент
сопротивления струи, а индексы s, r обозначают компоненты векторов относительно координатных ортов вдоль s и r соответственно.

Здесь Fi = giβΔT; Tw = Tw0 + γz; gs = g∙sinα; gr = g∙cosα; β = 3,665∙10–3, где Tw0 – температура на поверхности земли; g – ускорение свободного падения, ΔT – разность температур на оси струи и воздуха на соответствующей высоте.

К уравнениям (5.41)–(5.44) следует соотношения, связывающие координаты (s, r) с декартовыми координатами X, Z:

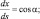(5.45)

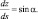(5.46)

Приведем также соотношения для :

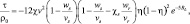(5.47)

где χ, χs – константы, функции η и Ri даются для каждого участка струи.

Система уравнений (5.41)–(5.46) решается при помощи гипотезы об автомодельности течения в турбулентных струях. Она состоит в том предположении, что распределения зависимых величин в различных сечениях струи подобны друг другу, т.е. описываются одними и теми же соотношениями.

Приведя уравнения (5.41)–(5.46) к безразмерному виду, вычисляя интегралы и производных, получаем систему обыкновенных дифференциальных уравнений в виде:

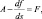(5.48)

где F, f – вектора правых частей и независимых переменных, а A – матрица коэффициентов.

Система (5.48) решается методом Рунге-Кутта последовательно для начального и основного участка струи.

Модельные расчеты характеристик струи приводилось нами для следующих начальных значений переменных: радиус сопла r0 = 0,5 м; начальная скорость выброса: v0 = 30 м/с; стратификация атмосферы: γ = 0,004 и –0,002 гр/м; скорость ветра W = 5 м/с; угол выброса α0 = 45° и 90°. Результаты расчета приведены на рис. 26, где указаны высота подъема и дальность выброса вредных веществ при аварий.

Известно, что зимой очень часто реализуются мощные приземные инверсии, простирающиеся до высот 1–1,5 км. В этих условиях, даже при наличии сдвига ветра атмосферная турбулентность практически отсутствует, что подтверждается с натурными наблюдениями, когда дымовой шлейф почти без изменения переносится на несколько километров. Таким образом, при земных инверсиях наша модель может работать, по крайней мере, до расстояний 1–10 км.

Летние ночные инверсии гораздо слабее зимних, они формируется после захода солнца и быстро разрушаются утром, кроме того, летний инверсионный слой часто неустойчив, в его толщине наблюдаются такие явления, как перемежающаяся
турбулентность, струйные течения, застой воздушных масс в складках местности, и т.д., так что область применимости струйной модели определяется местными факторами, и требует исследования конкретно для каждой местности.

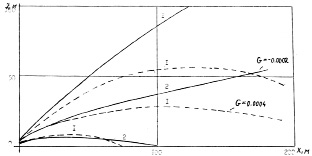
Рис. 26. Геометрия струи в условиях:
1 – температурной инверсии; 2 – в конвективных условиях

Далее, летом при ясной солнечной погоде формируется конвективный пограничный слой (КПС), который характеризуется не только развитой атмосферной турбулентностью, но и мощной ячейковой конвекцией. А из-за того, что атмосферная турбулентность не учитывалась при выводе основных соотношений теории, ее применение для расчетов струи в КПС, вообще говоря, неправомерно. Однако, как отмечалось в начале раздела, на малых расстояниях от источника, когда энергия турбулентности внутри струи больше атмосферной, эта модель еще применима, и масштаб применимости составляет десятки сот метров в зависимости от мощности выброса при одинаковых атмосферных условиях. Ячейковая конвекция имеет масштаб порядка ста метров и это расстояние будет являться масштабом области применимости нашей модели, если предыдущее рассмотрение даст расстояние большее ста метров.

Итак, коротко мы рассмотрели предельные состояния атмосферы, для которых модель струи применима наиболее полно и, наоборот, лишь вблизи от источника. На основании изложенного сделаем некоторые выводы:

1. В данном пункте показано, что распространение в атмосфере аварийных выбросов газа можно описать так называемой теорией турбулентных струй.

2. Область применимости струйной модели определяется в основном не геометрией источника, а состоянием атмосферы. Качественное рассмотрение состояний атмосферы показывает, что данная модель может успешно применяться в зимних инверсионных условиях до расстояний, по крайней мере, в несколько километров, а летом ночью и днем от десятков до сотен метров, причем эти расстояния существенно зависят от местной орографии, и должны, строго говоря, определяться в условиях конкретной местности.

3. Что касается прогноза концентрации продуктов сгорания, то грубо эту величину можно оценить, как