
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
1. СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ПРОЕКТИРОВАНИЯ СЕТЧАТЫХ ОБОЛОЧЕК ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ ПРИ ДИНАМИЧЕСКИХ НАГРУЗКАХ
Широкое внедрение композиционных материалов в различные отрасли народного хозяйства требует создания и совершенствования методов расчета и проектирования конструкций, в которых они применяются. Наиболее полных обзор методов расчета и проектирования конструкций из композиционных материалов представлен в работах
[3, 5, 10, 12, 13–18, 19, 24, 28, 29, 30, 33, 34, 35, 36, 56, 57, 64, 65, 71, 77, 86, 95, 114, 143–149] и др. Нужно отметить, что большинство известных методов в основном базируется на фундаментальных соотношениях механики сплошной среды. В то же время композиционные материалы обладают рядом специфических свойств, которые должны быть учтены при построении расчетных моделей и методов.
К этой специфике следует отнести то обстоятельство, что они являются существенно неоднородными, гетерогенными средами. Кроме того, их механические характеристики зависят от схемы расположения армирующих элементов и могут изменяться в широких пределах.
Поскольку процесс создания композиционных материалов тесно связан с изготовлением самой конструкции, открывается возможность создания материалов с заранее заданными свойствами, соответствующими характеру внешних нагрузок.
Следует иметь в виду также, что композиционным материалом присуща низкая жесткость и прочность при нагружении в направлениях, совпадающих с направлением армирования. Эта основная особенность композиционных материалов и является их основным недостатком. Сюда можно отнести и то, что несущая способность тонкостенных конструкций с традиционной схемой армирования для некоторых типов нагружения из-за сравнительно низкой изгибной жесткости часто исчерпывается задолго до достижения предельных нагружений (например, при потере устойчивости). Кроме того, в тех случаях, когда конструкций создаются путем последовательного наложения армированных слоев, для них характерен особый вид разрушения-расслоение, являющееся следствием слабого сопротивления материалов межслойному сдвигу и поперечному отрыву.
Как известно, для улучшения жесткостных характеристик композиционных материалов используются высокомодульные волокна многослойные конструкции и др.
В последнее время большое внимание привлекают композиционые материалы, армированные высокомодульными волокнами на основе углерода, бора и других элементов. свойства конструкционных материалов на основе бора и углепластиков с традиционным расположением волокон изложены в работах [144, 145, 190, 194, 202], где приведена подробная информация об основных направлениях работ американских авторов. Полученные результаты свидетельствуют о том, что армирование высокомодульными волокнами не приводит к пропорциональному росту всех упругих характеристик. Применение волокон бора и углерода увеличивает в основном жесткость материала в плоскости армирования.
Увеличение изгибной жесткости может быть достигнуто за счет повышения толщины и выбора рациональной схемы чередования слоев, но при этом проявляются низкие трансверсальные характеристики материала.
Опасность преждевременного разрушения композиционных материалов в результате нарушения межслоевых связей привела к идее создания пространственного каркаса из армирующих элементов.
В зависимости от принципа образования пространственных связей такие материалы можно разделить на три группы [62].
К первой относятся композиты, в которых пространственные связи образуется в результате искривления всех или части волокон одного направления. Эти материалы создаются рамках традиционной системы двух нитей: искривленных нитей основы и прямолинейных нитей «утка» [64].
Ко второй группе относятся материалы, в которых пространственные связи создаются за счет введения волокон третьего направления. Такие композиционные материалы образуется системой трех нитей в прямоугольной или цилиндрической системе координат. Волокно могут быть взаимно ортогональными и трех направлениях или располагаться под углом в одной их плоскостей армирования.
К третьей группе относятся композиты, которые пространственные связи создаются нитевидными кристаллами. Такие материалы образуется при использовании вискеризованных волокон, лент или тканей. Особенность этих материалов заключается в характере расположения нитевидных кристаллов относительно направления основной арматуры и наличии жесткой или податливой связи между волокнами и нитевидными кристаллами. Указанная особенность обуславливается выбором способа вискеризации арматуры. Все эти три направления развиваются параллельно и успешно дополняют друг друга. Остановимся на анализе работ, выполненных в этих направлениях.
Сведения о свойствах и принципах построения пространственно-армированных материалов изложены в работах [125, 126, 143, 145, 180]. Наиболее полный обзор соответствующих исследований можно получить в монографии Жигуна И.Г. и Полякова В.А. [62]. В ней каждого типа пространственных композитов приведены кривые деформирования при нагружении в главных осях и под углом к ним, расчетные модели, инженерные формулы для расчета упругих характеристик и численные оценки компонент матриц прочности и жесткости при растяжении-сжатии, изгибе и сдвиге. При разработке теории армированных сред с пространственной укладкой волокон необходимо учесть ограничения, которые накладываются на объеме содержание армирующих элементов в материале. Введение поперечных связей ведет к уменьшению содержания волокон в плоскости армирования. Поэтому при оценке эффективность пространственного армирования необходимо учитывать не только степень роста трансверсальных характеристик и модуля упругости при нагружении в плоскости основного армирования.
Одним из способов пространственного армирования, позволяющим повысить изгибную жесткость материала при сохранении высоких свойств жесткости и прочности в плоскости основной укладки волокон, является объемная структура. Оболочка с такой схемой формирования является эффективной в роли элемента конструкции, в котором одновременно с высокими механическими свойствами в плоскости армирования должна быть необходимая жесткость при поперечной нагрузке или высокая сопротивляемость потере устойчивости. Такая пространственная структура может быть образована намоткой [выкладкой] или формированием. Технология изготовления такой структуры была разработана американскими учеными и описана в работах [182, 183, 186]. Исследованию технологических процессов изготовления элементов конструкции летательных аппаратов из нового композиционного материала (тетраструктура) в нашей стране посвящены работы [64, 65].
В них показано, что при изготовлении конструкции методом непрерывной намотки нити или узкой ленты, пропитанных связующим, ленты последующего слоя укладываются со сдвигом по отношению к предыдущему, при этом три системы ребер образуют при пересечении правильные тетраэдры и октаэдры. Представленная пространственная структура характеризуются следующими параметрами: размерам ячейки (длина ребра тетраэдра), толщина и строительной высотой ребра.
Конструкции, выполненные из композиционного материала с рассмотренной пространственной структурой армирования, могут найти самое широкое применение. Обладая большой изгибной жесткостью и сопротивляемостью к потере устойчивости, такая объёмная структура может применяться в несущих тонкостенных конструкциях.
Описанная выше пространственная структура представляет собой некоторую сетчатую конструкцию.
Исследование напряженно-деформированного состояния сетчатых пространственных конструкций может быть осуществлено на основе трех возможных подходов [118]. Первый подход состоит в использовании соответствующих методов расчета пространственных рам (в случае жесткого сопряжений).
Второй подход основан на дискретизации сетчатой системы путем разделения ее на естественные или обобщенные конечные элементы с последующим описанием поведения системы конечно-ранообразными управлениями.
Третий подход заключается в замене сетчатой конструкции которой условной однородной сплошной среды. В этом случае необходимо сначала определить соответствующие упругие свойства эквивалентной сплошной конструкций, а затем рассчитать эту конструкцию в соответствий с заданными нагрузками и краевыми условиями. Определив усредненные силовые и деформационные характеристики, можно далее вернуться к сетчатой системе с учетом работы отдельных ее элементов. Преимуществом этой модели является то что при расчете и проектировании могут быть использованы известные решения для сплошных оболочек различных форм и с различными схемами нагрузки.
Рассмотрим более подробно все три подхода. В первом случае рассматривается сетчатая оболочка в виде пространственной рамы или формы. Расчет разводят методом сил, методом перемещения или смешанными методами, строительной механики стержневых систем.
Условия равновесия узлов и управления совместной деформации элементов приводят к необходимости решения систем алгебраических уравнений.
Вопросы расчета сетчатых конструкции как пространственных рам рассмотрены в работах [31, 32, 47, 72, 110, 195].
Методы расчета стержневых пространственных систем с шарнирным сопряжением элементов приведены в работах [48, 82, 83, 155, 156, 172, 173].
Большинство работ этого направления используют матричную формулировку метода сил. К числу основных работ в этой области следует отнести работы Фалькенгейнера [184, 185], Лайгенфорса [203], Аргириса [8, 175, 176], Смирнова А.Ф. [137, 138] и др.
Основные положения метода сил в матричной формулировке применительно к системе, состоящей из ребер, образующих ортогональную сетку, приведены в работах [75, 76, 184, 185]. Приводится вывод матрицы податливости конструкции и отмечается важность выбора в качестве неизвестных самоуравновешанных систем усилий. Исходя из принципа наименьшей работы, получена система линейных алгебраических уравнений относительно неизвестных усилий. Примеры расчетов статических неопределимых систем с большим числом неизвестных приведены в работах [3, 84, 88, 134, 167].
В серии работ Аргириса [8, 175, 176] применительно к конструкциям самолета использован дискретный матричный метод.
Работы Смирнова А.Ф. [137, 138] посвящены применению матричных методов для решения задач устойчивости и колебаний сетчатых стержневых конструкций.
Решение задач строительной механики систем с применением ЭВМ отражены в работах [43, 51, 77, 78, 82, 83, 122, 161–166].
Алгоритмы формирования коэффициентов канонических уравнений метода сил для пространственной системы предложены в работе [137, 138]. Матричная форма метода перемещений для расчета сетчатой цилиндрической оболочки, стержни которой жестко соединены в узлах и имеют постоянные сечения, использовано в работе [91].
Этот алгоритм, реализованный на ЭВМ, позволяет рассчитывать рассматриваемые оболочки с защемленными продольными краями и торцевыми диафрагмами.
Метод, разработанный Лебедевым В.А. [80], позволяет рассчитать пространственные стержневые системы, имеющие циклическую симметрию. На основе проведенные в работе [51] исследование для различных сетчатых конструкций могут быть заранее составлены простейшие типовые матрицы коэффициентов системы канонических уравнений.
Работы [43, 64, 70, 168] посвящены расчету матричным методом различного типа оболочек с ортогональной сеткой ребер.
Для статистического расчета регулярных сетчатых систем в работах [70, 91, 116] используется метод конечных разностей.
В последнее время для расчета сетчатых конструкций применяется метод конечных элементов. Для расчёта произвольных стержневых систем регулярной структуры в работе [82] предложен метод расчета, близки к методу конечного элемента. Матрица жесткости коэффициентов для каждого элемента определяется путем расчета его узлов на единичные перемещения. С помощью полученных матриц записываются уравнения равновесия в перемещениях.
Наиболее распространённым является третий подход к определению напряженно-деформированного состояния сетчатых конструкций, который основан на использовании континуальной расчетной схемы. После континуализации расчет сетчатых систем принципиально не отличается от расчёта сплошных конструкций. Связи с этим позволяется возможность использования многих известных результатов и методов теории гладких оболочек для расчета сетчатых конструкций. Контитуальная расчетная схема, как правило, приводит к наиболее простому решению, причем в ряде случаев это решение удается представить в замкнутой аналитической форме.
Сетчатые оболочки впервые начали применять в перекрытиях различного вида, поэтому большинство работ по сетчатым оболочкам, использующим континуальный подход, посвящено расчету и проектированию большепролетных конструкций [37, 101, 152].
Расчет сетчатых оболочек как континуальных конструкций изложен в работах [76, 91, 92, 101, 112, 113]. В работе [91] дано сравнение решений, использующих дискретную схему с решением по континуальной теории. Показано что разница в результатах расчетов не слишком велика.
В работах [112, 120, 152] при расчете сетчатых конструкции по континуальной схеме за расчетную модель принята однородная ортотропная оболочка. В работе [92] приведен расчет сетчатых оболочек, основанный на вариационном методе Власова В.З. [38]. В работах [76, 78, 171, 174, 195, 203] к расчету сетчатых безмоментных оболочек. Области применения континуальных расчетных схем для сферических оболочек даны в работах [112, 171]. Показано, что континуальная модель применима при расчете дискретных систем, в которых наибольшая длина стержня меньше одной трети радиуса кривизны оболочки.
Сетчатая оболочка, состоящая из разносторонних треугольников, может быть приведена к изотропной оболочке со следующими оболочками [112, 118]:
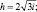
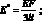
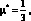
|
где h,μ E – |
соответственно толщина, коэффициент Пуассона и модуль упругости материала эквивалентной сплошной оболочки; |
|
F, i, l, E – |
соответственно площадь, радиус инерции поперечного сечения ребра, длина между узлами, модуль упругости материала стенки. |
В работах [178, 200] жесткости стержней на изгиб в плоскости касательной к середине поверхности и на кручение принимались равными нулю.
Метод расчета сетчатых оболочек, разработанный Г.И. Пшеничновым [101, 112] на основе континуальной расчетной схемы, основан на рассмотрении их в виде сплошных оболочек, обладающих свойствами конструктивной анизотропии. Полученная система уравнений равновесия сводится к одному уравнению относительно разрешающей функции. Решение ведется в виде одинарных или двойных тригонометрических рядов.
Система, образованная ребрами двух направлений, может быть геометрически изменяемой, когда жесткость ребер на изгиб в плоскости касательной к срединой поверхности и кручение не учитывается. Это следует из приведенного Пшеничновым Г.И. анализа соотношений упругости. Система становится геометрически неизменяемой при соответствующих условиях закрепления контура оболочки. В работе [102] приведет расчет сетчатой сферической оболочки. Для сферической оболочки с квадратной сеткой, жестко заделанной по контуру, получено приближенное решение в замкнутой форме.
В последнее время опубликован ряд работ по теории сетчатых оболочек, построенной Пшеничновым Г.И. К ним относятся исследования пологих сферических, цилиндрических, гиперболических и других оболочек [1, 75,7 6, 136]. Для сетчатых оболочек вращения в некоторых случаях могут применяться методы расчета на моделях, предложенных в работах [112, 155].
Энергетический метод расчета сетчатых оболочек использован в работах [112, 178].
Изучение собственных колебаний, подкрепленных в осевом направлении цилиндрических оболочек, посвящены работы Бреславского В.Г. [27], Григолюка Э.И. [53, 54]. Расчет собственных колебаний, подкрепленных оболочек освещены в работах Заруцкого В.А. [6, 7, 66] и обзорных статьях [7], где можно найти подробный обзор литературы, посвященной этому вопросу. Колебания сетчатых оболочек настоящее время исследованы относительно мало. Следует отметить работы [17, 105, 106], в которых получены решения некоторых задач о свободных колебаниях пологих оболочек, рассмотренных как контитуальные системы. Некоторые вопросы динамического расчета стержневых систем рассмотрены в работах [70, 112, 113].
Большинство задач о колебаниях сетчатых оболочек рассмотрено на основе теории изотропных оболочек [84, 113, 106, 112].
Их последних работ по исследованию безмоментных колебаний следует отметить работы Лужина О.В. [84, 85], Росса М.Л. [130], Ке Чжи [169], Пшеничного [101–112].
Работы Пшеничного Г.И. [101–112] посвящены расчету свободных и вынужденных колебаний сетчатых оболочек с разносторонней треугольной сеткой, выполненной из стержней одинакового поперечного сечения. В [101–112] автором разработан асимптотический метод интегрирования дифференциальных уравнений, описывающих колебательный процесс оболочек вращения, являющийся аналогом асимптотического метода Гольденвейзера А.Л. [49, 50] для статической задачи. Проводится сравнение с точным результатом, полученным Лужиным О.В. [84, 85]. Предлагается классификация форм свободных колебаний оболочек вращения для случая, когда число узловых линий, проходящих вдоль меридиана, не слишком велико.
В работах [106, 112, 113] показано, что при определении нижних частот колебаний пологих сетчатых оболочек можно учитывать лишь поперечные колебания. Для оболочек большого прогиба [200] необходимо учитывать все составляющие инерционных сил.
Перечисленные выше работы посвящены расчету и проектированию сетчатых конструкций из традиционных материалов. Применение композиционных материалов вызывает необходимость учета их специфических особенностей. Кроме того, наличие пространственной структуры требует создания теоретических методов исследования колебаний подобных конструкций. Многие из описанных в литературе методов построены на ряде допущений, которые при расчете сетчатых конструкции из композиционных материалов могут привести к существенным погрешностям.
В целом проведенный обзор литературы по исследуемому вопросу позволяет сделать вывод о том, что в современной литературе отсутствую законченные исследования свободных и вынужденных колебаний сетчатых оболочек. Тем более, практически отсутствуют работы, посвященные исследованию колебаний таких специфических конструкций, как оболочки тетрагональной структуры.
Целью монографии является развитие аналитических методов и создание инженерных методик динамического расчета оболочек с тетраструктурой, являющихся однним из основных конструктивных элементов перспективных конструкций типа самолетов и ракет.