
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
2.1. Определение динамических упругих постоянных с использованием сплошной модели
Рассмотрим в качестве расчетной модели тетрагональной структуры некоторую сплошную оболочку. При этом будем полагать, что срединные поверхности оболочки тетрагональной структуры и ее расчетной модели совпадают. Также совпадают деформации стержней оболочки тетрагональной структуры с соответствующими деформациями исследуемой оболочки.
Будем полагать, что сплошная оболочка представляет собой шарнирно-опертую цилиндрическую ортотропную оболочку длиной L, радиусом R, толщиной h. Для такой оболочки в работе [5] получены следующие выражения для спектра собственных частот
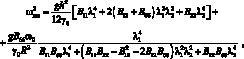 (2.1)
(2.1)
|
где g – |
ускорение силы тяжести; |
|
γ0 – |
удельный вес материала оболочки; |
|
L – |
длина оболочки; |
|
m, n – |
целые числа, определяющие число полуволн в продольном и поперечном направлениях соответственно; |
|
ω – |
частота колебаний; |
|
Bij – |
компоненты тензора модулей упругости, которые выражаются через технические упругие постоянные следующим образом: |
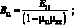
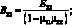
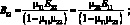 (2.2)
(2.2)
B66 = G12.
Причем Е11, Е22 – линейные модули упругости; µ11, µ22 – коэффициенты Пуассона.
В выражение (2.1) входят пять значений упругих постоянных (Е11, Е21, µ11, µ22, G12), которые и являются искомыми величинами. Таким образом, для решения поставленной задачи требуется знать пять первых собственных частот колебаний оболочки.
Из (2.1) после некоторых преобразований с учетом (2.2) легко получить
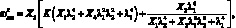 (2.3)
(2.3)
где
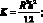
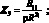
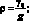
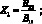
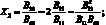
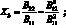
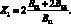
Ограничиваясь рассмотрением достаточно низких частот колебаний, можно положить m = 1, и варьируя значением выражения n, определяющим число волн по окружности с учетом значения (2.2) из (2.3), получим выражение
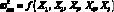 . (2.4)
. (2.4)
Определив экспериментально пять первых собственных частот колебаний ωі, соответствующих различным значениям, получим пять алгебраических уравнений с пятью неизвестными
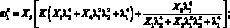 (2.5)
(2.5)
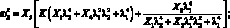
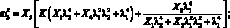
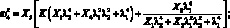
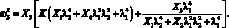
Для решения системы нелинейных уравнений (2.5) на ЭВМ воспользуемся методом Ньютона [58].
Определив величины X1, X2, X3, X4, X5 из (2,5) с учетом (2.3), определим упругие постоянные по формулам:
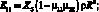
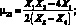
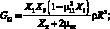
E22 = E11X1;
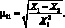 (2.6)
(2.6)
Найденные для данного типа оболочки значения динамических упругих постоянных представлены табл. 2.1. Заметим, что эти характеристики относятся к сплошной модели ортотропной оболочки.
Представляет практический интерес определение упругих постоянных у цилиндрических сетчатых оболочек из КМ. Для получение для частотного уравнения сетчатых оболочек необходимо вывести основные соотношения, учитывающие наличие тетрагональной структуры.