Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

2.2. Основные соотношения теории оболочек тетрагональной структуры (ОТС)

Предположим, что для оболочек тетрагоналной структуры справедливы гипотезы Кирхгофа-Лява о жестком нормальном элементе.

В соответствии с гипотезами Кирхгофа-Лява в законе Гука следует пренебречь напряжениями σγ по сравнению σα и σβ. Таким образом, в качестве основного элемента оболочки размаривать элемент срединой поверхности, нагруженный усилиями и моментами.

Рассмотрим задачу определения частоты свободных колебаний оболочек тетрагональной структуры из КМ. Исходную систему дифференциальных уравнений получим из уравнений классической теории для круговых цилиндрических оболочек с учетом инерционных сил, лишь в направлении нормального перемещения.

Уравнения равновесия согласно [5,17,36]:

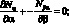
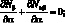
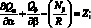
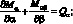
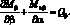(2.7)

Формулы, связывающие компоненты деформаций с компонентами перемещений [17].

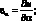
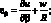
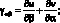(2.8)

.

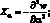
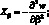
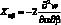Соотношение упругости [28]:

Nα = B11εα + B12εβMα = C11Xα + C12Xβ;

Nβ = B12εα + B22εβMβ = C12Xα + C22Xβ; (2.9)

Nαβ = B33γαβMαβ = C12Xαβ,

где выражение для жесткостей имеют вид:

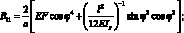
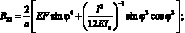(2.10)

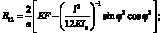
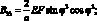
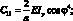
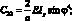
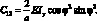
Рассматриваем только спиральные ребра симметричной структуры пакета, где α – расстояние между осями стержней; l – длина стержней.

Уравнение неразрывности:

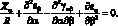(2.11)

Поставляя значения компонентов деформации εα, εβ, γαβ, Xα, Xβ, Xαβ соответственно из (2.8) в соотношение упругости (2.9), получим выражения для внутренних сил и моментов, представленных с помощью перемещении u, v, w.

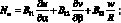
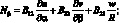
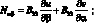
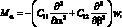(2.12)

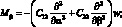
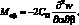
Подставляя значения моментов из (2.12) в последние два уравнения равновесия (2.7), получим для поперечных сил следующие выражения:

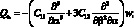(2.13)

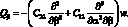
Подставляя значения внутренних сил Nα, Nβ, Nαβ и Qα, Qβ соответственно из (2.12) в первые три уравнения равновесия (2.7)

В такой постановке получили следующую систему уравнений равновесия в перемещениях:

L11(Bik)u + L12(Bik)v + L13(Bik)w = 0;

L21(Bik)u + L22(Bik)v + L23(Bik)w = 0; (2.14)

L31(Bik)u + L32(Bik)v + L33(Bik, Сik)w = 0,

где для линейных дифференциальных операторов имеем:

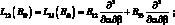
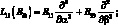
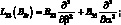(2.15)

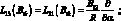
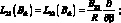
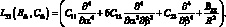
Уравнения (2.14) представляет собой соотношения технической теории цилиндрических оболочек тетрагональной структуры, записанные в перемещениях.

Уравнения технической теории цилиндрических оболочек тетрагональной структуры могут быть представлены в форме уравнений смешанного метода [38]:

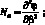
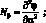
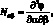(2.16)

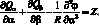(2.17)

Решая соотношения упругости (2.9) относительно компонентов деформации εα, εβ, γαβ, получим:

εα = A11Nα + A12Nβ;

εβ = A22Nβ + A12Nα; (2.18)

γα,β = A66Nαβ,

где для коэффициентов, характеризующих упругие свойства оболочки имеем:

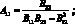
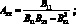(2.19)

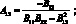
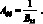
Подставляя полученные при этом (2.18) совместно с (2.8) в уравнение неразрывности (2.11), получим;

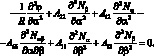(2.20)

Из трех последних уравнений (2.7) и уравнения неразрывности(2.20) с учетом (2.13) получим следующую разрешающую систему дифференциальных уравнений:

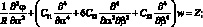
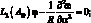(2.21)

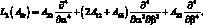
К системе уравнений (2.21) следует присоединить граничные условия, которые для шарнирно-опертой оболочки запишутся следующим образом:

при α = 0, α = L w = v = Mα = Nα = 0.

Решение системы (2.21) представим в форме [5.17]:

φ(α, β, t) = Fmn sin λ1α sin λ2β cos ωmnt;

w(α, β, t) = Фmn sin λ1α sin λ2β cos ωmnt, (2.22)

где Fmn, Фmn – некоторые постоянные

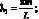
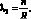
Легко заметить, что уравнения (2.22) полностью удовлетворяют граничными условиями.

Подставляя (2.22) в систему (2.21), получим однородную систему уравнений относительно Fmn и Фmn:

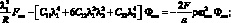(2.23)

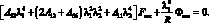
Приравнивая к нулю определить однородной системы уравнений (2.23), получим формулу для нахождения частот собственных колебаний оболочки тетрагональной структуры:

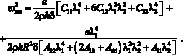(2.24)

В качестве примера, рассмотрим оболочку по найденным экспериментальном данным частота ω = 395 Гц, соответствует параметрам волнообразования m = 1, n = 4. Параметры оболочки берутся такими же, как в эксперименте, т.е. φ = 15°; R = 10,3∙10–2 м; h = 2,5∙10–3 м; δ = 1,5∙10–3 м;
L = 17,5∙10–2 м, l = 4,75∙10–2 м.

Пользуясь вышеизложенной методикой, с помощью соотношения (2.24) получены следующие значения модуля упругости Е для материала оболочки: E = 3,5∙1010 H/м2.

Для определения эффективного модуля упругости и коэффициента Пуассона имеем [95]:

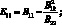
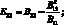G = B33;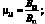 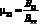(2.25)

с учетом формул

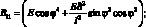
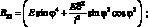(2.26)

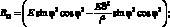
B33 = E sin φ2 cos φ2.

После этого по назначению (2.25) вычислены упругие постоянные для угла φ = 15°, которые сведены в табл. 2.1.

Расчетные зависимости эффективного модуля упругости от угла φ показаны на рис. 2.2.

Таблица 2.1

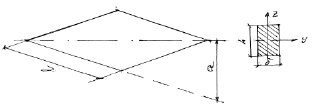
Рис. 2.1

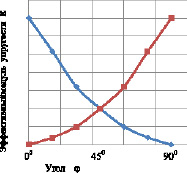
Рис. 2.2