
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
2.4. Определение упругих констант материала на основе рассмотрения элементарной ячейки оболочки
Рассмотрим другой подход к определению механических характеристик оболочек из композиционных материалов, позволяющих не только вычислить основные механические характеристики оболочки, но и определить их зависимость от геометрических параметров, размеров ячейки и углов между ребрами.
Для решения этой задачи выделим из оболочки одну ячейку (см. рис. 2.4) g, которая представляет собой ромб с размерами а, b и внутренним углом 2φ. Ее расчетная схема в виде рамы показано на рис. 2.5.

Рис. 2.4. Сетчатая оболочка
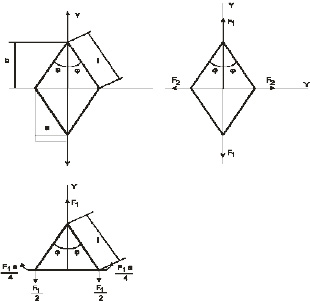
Рис. 2.5. Расчетная схема рамы
Сначала рассмотрим статистически неопределимую раму под действием только силы F1. Для раскрытия статической неопределимости используем метод сил.
Записывая каноническое уравнение метода сил и вычисляя его коэффициенты, можно определить все внутренние силовые факторы, возникающие в сечениях рамы, состоящие из изгибающего момента 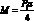 и растягивающего усилия
и растягивающего усилия 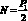 .
.
Дальнейшее решение задачи сводит к определению изменений диагоналей ромбы, иначе говоря, к определению перемещения точек А, В, С, Д, относительно диагоналей.
Поставленная задача легко реализуется с помощью известных из курса сопротивление материалов интегралов Мора.
Из рис. 2.6 следует
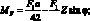
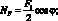
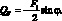 (2.28)
(2.28)
Единичные силовые факторы при этом записываются:
По оси X
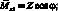

 (2.29)
(2.29)
По оси Y
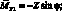

 (2.30)
(2.30)
С учетом (2.28), (2.29) и (2.30) определяем перемещение по оси X отсилы F1:
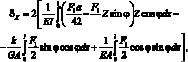 (2.31)
(2.31)
где a = l sin φ.
Для прямоугольника с размером 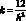 и учитывая, что для композитных материалов [95] G = 0,1E получим:
и учитывая, что для композитных материалов [95] G = 0,1E получим:
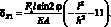 (2.32)
(2.32)
Аналогично от силы F2 определим перемещения по оси Х:
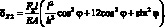 (2.33)
(2.33)
На основе (2.29) и (2.30) определим перемещения по оси Y от силы F1 и F2 аналогично (2.31):
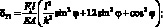 (2.34)
(2.34)
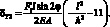
Относительные перемещения по оси Y от силы F1 и F2 будут:
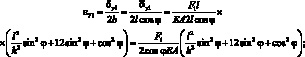
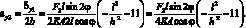 (2.35)
(2.35)
Относительные перемещения по оси Х от силы F1 и F2 будут:
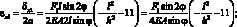
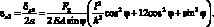 (2.36)
(2.36)
Поскольку в цилиндрической оболочке нагруженной внутренним давлением, кольцевые напряжения вдвое превышают осевые [95], можно считать, что F1 = 2F2 с учетом этого:
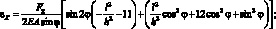
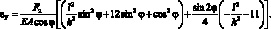 (2.37)
(2.37)
Согласно определению коэффициента Пуассона получим, что приведенный коэффициент поперечной деформации  определяется следующим выражением:
определяется следующим выражением:
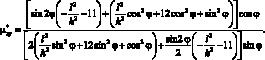 (2.38)
(2.38)
Для определения модуля упругости Е оболочки сначала вычислим продольную деформацию одной ячейки (g) оболочки, от силы F2
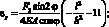
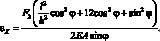 (2.39)
(2.39)
Рассмотренный элемент оболочки (g) можно предоставить как панель с размерами 2a, 2b и толщиной 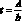
Тогда его продольная деформация определится из соотношения Коши, при σу = 0
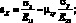
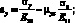 (2.40)
(2.40)
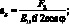
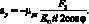
Приравнивая (2.37) и (2.40) получим:
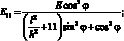
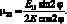 (2.41)
(2.41)
Из условий симметрии
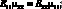
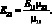 (2.42)
(2.42)