
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
3.3. Функции динамической податливости стержневых элементов каркаса
Перемещения стержней с номерами і, работающих в составе каркаса, складываются из перемещений от действующей на них нагрузки и перемещений от реакции связанных с ним элементов каркаса, направленных под углом – φ к его оси, и имеют вид:
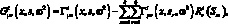 (3.17)
(3.17)
|
где |
реакция связей в точках Sm; |
|
k – |
число точек связи. |
Амплитудные перемещения произвольного j-го элемента каркаса, направленного под углом –φ, равны.
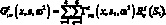 (3.18)
(3.18)
Из условий совместности перемещений элементов каркаса в точках связи получим
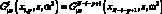 (3.19)
(3.19)
или
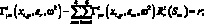
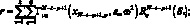
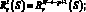 (3.20)
(3.20)
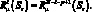
Раскроем выражение, подставив значения функции динамической податливости элементов каркаса:
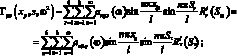 (3.21)
(3.21)
τ = r; θ = N – i – p + 1;
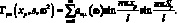
С целью дальнейшего упрощения (3.21) подставим координаты точек соединения стержней:
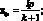
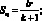
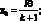
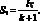 (3.22)
(3.22)
С учетом (3.22) функцию динамической податливости і-го стержня можем записать в виде:
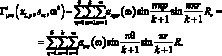 (3.23)
(3.23)
Так как синус является периодической функцией, то:
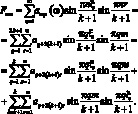 (3.24)
(3.24)
Пусть h = 2k + 2l тогда
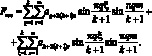 (3.25)
(3.25)
Из выражения (3.24) для amn следует
a–h+2(k+1)(s+1) = ah–2(k+1)(s+1) = a(h+2(k+1)(s+1). (3.26)
Таким образом:
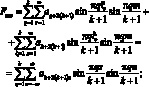 (3.27)
(3.27)
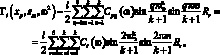 (3.28)
(3.28)
где
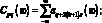
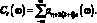 (3.29)
(3.29)
Теперь умножим левую и правую части нашего уравнения на 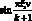 и просуммируем по ξ от 1 до k
и просуммируем по ξ от 1 до k
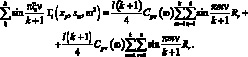 (3.30)
(3.30)
При этом использовались известные соотношения [158]:
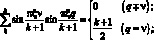 (3.31)
(3.31)
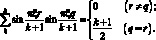
Это соотношение, иногда называемое свойством арифметической ортогональности, впервые было получено в работе [59] и использовано для решения задачи о колебаниях регулярных систем[158]:
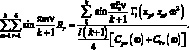 (3.32)
(3.32)
Вернемся к рассмотрению (3.17) с учетом (3.32). при этом выражения для функции динамической податливости стержня, соединенного со стержнем под углом φi приобретает вид:
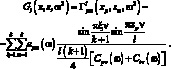 (3.33)
(3.33)
или, раскрыв выражение Гi(xp, sm, ω2) по формуле (3.17), после некоторых преобразований, получим:
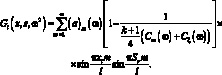 (3.34)
(3.34)
Таким образом, будем считать решенной задачу о вынужденных колебаниях свободно опертого i-го стержня, соединенного со стержнями, направленными под углом –φ к оси α, так как амплитудные перемещения от произвольной нагрузки при известной ФДП могут быть определены интегральной сверткой G(x, s, ω2) от функции нагрузки:
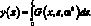 (3.35)
(3.35)
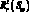 –
–