
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
3.4.1. Построение функции динамической податливости в осевом направлении (P1)
Пусть оболочка нагружена единичной гармонической силой по направлению оси α. Компоненты функций динамической податливости цилиндрической сетчатой оболочки, относительно системы криволинейных координат α, γ, β определяются следующими выражениями:
для і-го стержня:
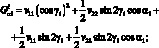
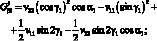
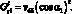
Для j-го стержня: (3.37)
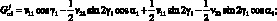
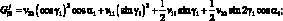
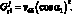
Из условий совместности деформации:
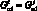
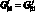
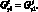 (3.38)
(3.38)
Согласно (3.13), (3.14) и (3.20) для цилиндрических сетчатых оболочек имеем:
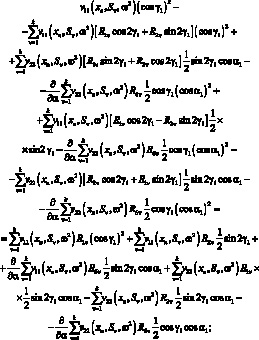 (3.39)
(3.39)
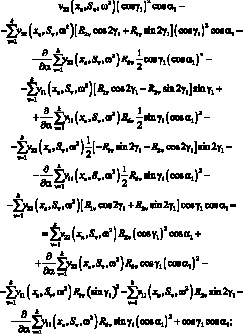 (3.40)
(3.40)
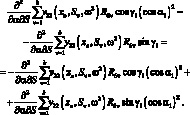
Постановка (3.11) и (3.16) в (3.39) приводит к системе уравнений относительно R1ν, R2ν, R6ν:
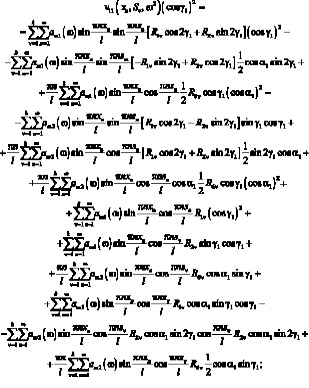
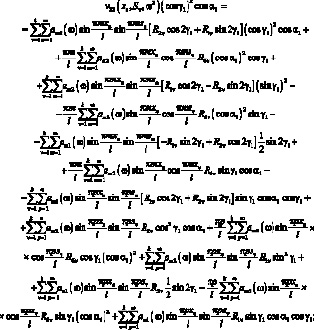
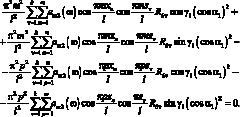
Поставим координаты точек стержней і и j, т.е.
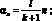
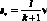
и умножим левую и правую части этой системы на 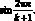
Затем просуммируем по n от 1 до к с учетом (3.31). После этого умножим третье уравнение на 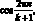 принимая во внимание:
принимая во внимание:
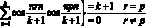 (3.41)
(3.41)
и после несложных преобразований получим систему трех алгебраических уравнений относительно неизвестных реакции R1ν, R2ν, R6ν.
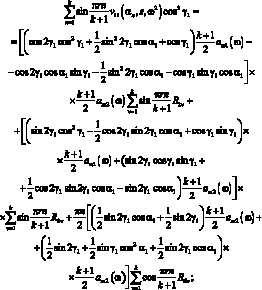
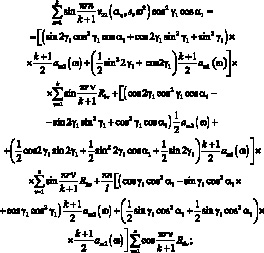 (3.42)
(3.42)
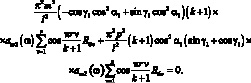
Проблема отыскания частот собственных колебаний цилиндрических сетчатых оболочек из системы (3.15) в принципе не вызывает затруднений. Для ее решения приравниваем определитель к нулю.
Из условия нетривиальности решения, имеем:
 (3.43)
(3.43)
где через Aij обозначены следующие выражения:
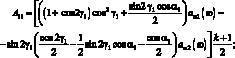
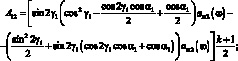
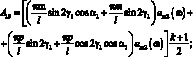
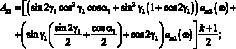
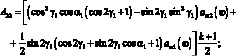
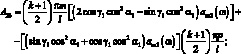
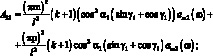 (3.44)
(3.44)
здесь
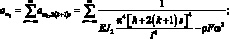
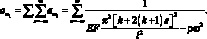 (3.45)
(3.45)
Бесконечный числовой ряд в этих выражениях может быть просуммирован при помощи теории вычетов.