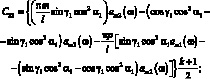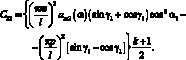Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ

Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,

3.4.2. Построение функции динамической податливости в тангенциальном направлении (P2)

Пусть оболочка нагружена единичной гармонической силой по направлению оси α. Аналогично предыдущему определяем амплитудные перемещения.

Для стержни под углом φ:

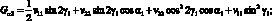
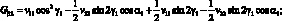
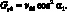(3.46)

Остальные перемещения равны нулю.

Для стержни под углом – φ:

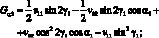
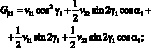
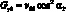(3.46′)

Из условий совместности деформации и с учетом знаний ФДП (3.13), (3.14) и (3.20) получим систему алгебраических уравнений относительно R1ν, R2ν, R6ν. Опуская некоторые промежуточные выкладки, аналогичные выкладкам, проделанным в 3.4.1 получим:

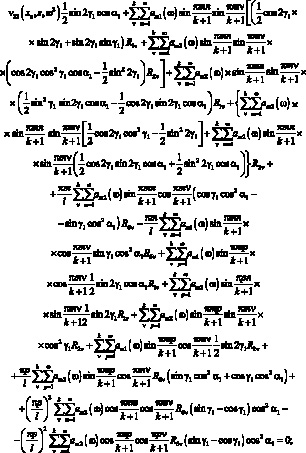
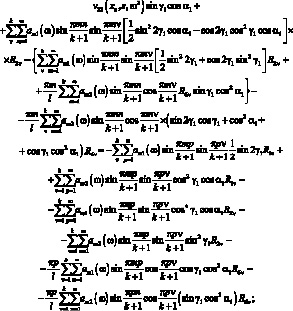
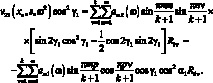(3.47)

Первое и второе уравнение системы умножим на 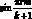и просуммируем по m от 1 до k, с учетом (3.31), а третье уравнение на 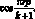Постановка (3.41) в формулы (3.47) приводит к следующим выражениями:

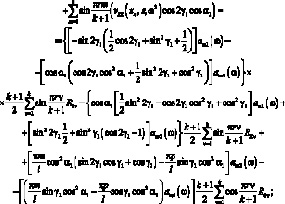(3.48)

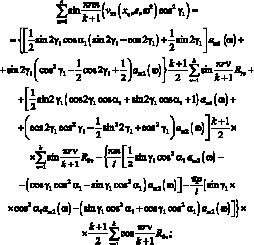
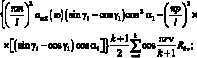
Из условия нетривиальности решения, имеем:

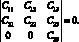(3.49)

где

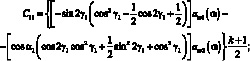
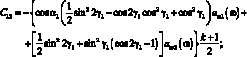
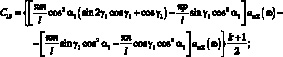
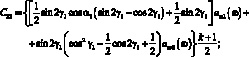
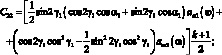(3.50)