
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ДИНАМИЧЕСКОЕ ПОВЕДЕНИЕ ОБОЛОЧКИ ИЗ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ тетрагональнОЙ СТРУКТУРЫ
Немеребаев М. Н., Бекмуратов М. М., Орынбаев С. А., Актаев Е. К.,
4.5. Устойчивость оболочек тетрагональной структуры из км, обтекаемых сверхзвуковым потоком газа
Расчет сетчатых и подкрепленных оболочек как систем, имеющих сложную структуру, вызывает вычислительные и принципиальные трудности. Их разрешение на основе уточнения классической теории оболочек с применением новых модельных представлений и подходов, совершенствования методов и методик расчета является одной из самых актуальных проблем механики оболочных конструкций и представляет несомненный прак-
тический интерес.
Рассмотрим круговую сетчатую цилиндрическую оболочку бесконечной длины, закрытую непроникаемой плёнкой и обтекаемую сверхзвуковым потоком газа с невозмущённой скоростью u, направленной вдоль образующих оболочек, т.е. по координа-
там α (рис. 4.10)
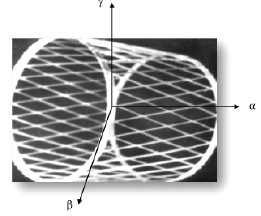
Рис. 4.10. Цилиндрическая сетчатая оболочка из КМ
Предполагая, что давление газа Р на обтекаемую поверхность оболочки через плёнку может быть вычислено при помощи приближенной формулы поршневой теории [36 ]
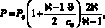 (4.70)
(4.70)
|
где P0 – |
давление невозмущённого потока газа; |
|
ϑ – |
нормальная составляющая скорости потока газа, обтекающего поверхность оболочки; |
|
c0 – |
скорость звука в невозмущенном газе; |
|
ﬡ – |
показатель политропы. |
Следуя работам [39, 40], будем считать, что u ≤ c0 и, разложив уравнение (4.70) в ряд по формуле бином Ньютона для малых возмущений, в первом приближении c учетом 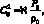 будем иметь:
будем иметь:
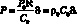 (4.71)
(4.71)
Рассмотрим линеаризованное течение газа вдоль оболочки, по которой распространяются упругие волны. В этом случае:
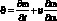 (4.72)
(4.72)
и следовательно, по формуле избыточного давления
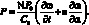 (4.73)
(4.73)
Кроме того, примем во внимание линейное демпфирование ε.
Тогда получим следующие динамические уравнения для цилиндрической сетчатой оболочки, обтекаемой сверхзвуковым потоком газа а направлении α.
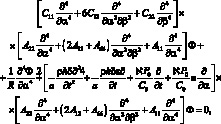 (4.74)
(4.74)
где a – расстояние между осями стержней,и согласна (4.19 ) принимаем:
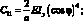
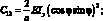 (4.75)
(4.75)
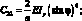
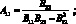
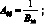
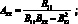
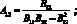
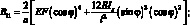
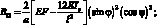 (4.76)
(4.76)
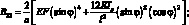
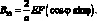
Решение уравнения (4.74) ищем в виде волн, распространяющихся по поверхности оболочки:
 (4.77)
(4.77)
|
где Ф0 – |
некоторая комплексная постоянная; |
|
ω – |
частота колебаний оболочки; |
|
|
волновое число; |
|
λ – |
целое число волн в окружности поперечного сечения оболочки; |
|
n – |
длина полуволны в направлении образующей оболочки. |
Подставляя значения (8) в исходное уравнение (4.74), придём к следующему характерному уравнению:
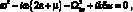 (4.78)
(4.78)
где 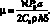
А для квадрата частоты собственных поперечных колебаний оболочки 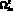 имеем:
имеем:
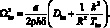 (4.79)
(4.79)
Здесь принято:
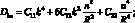
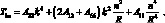 (4.80)
(4.80)
Если мнимая часть частоты колебаний отрицательна (Imω < 0), то движение оболочки устойчиво [5, 21, 40].
Если же мнимая часть колебаний (Imω > 0) положительная, то невозмущённое движение устойчиво, лишь по отношению к малым возмущениям.
Таким образом, из условия Imω ≥ 0, для скоростей невозмущённого потока газа, при некотором невозмущенное движение оболочки устойчиво, получим неравенство:
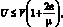 (4.81)
(4.81)
где 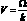 является фазовой скоростью распространения упругих волн в оболочке. Тогда:
является фазовой скоростью распространения упругих волн в оболочке. Тогда:
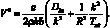 (4.82)
(4.82)
Второй член последнего уравнения представляет собой конструктивное демпфирование.
Из неравенства (4.81) для критической скорости получим
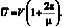 (4.83)
(4.83)
Как видно из (4.75), коэффициенты упругости Cik и Bik зависят от угла φ.
В силу этого, из (4.81) и (4.82) следует, что критическая скорость невозмущенного потока зависит от распространения стержней в теле оболочки.
Если же устойчивость теряется по несимметричной форме, то учитывая, что n2 мало по сравнению m2 = kR, членами 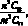
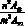 можно пренебречь.
можно пренебречь.
Тогда критическая скорость, принимающая минимальное значение в близи m и n, удовлетворяет уравнение
C11m2A22m2 – R2A22m = 0. (4.84)
В этом случае для критической скорости получим следующую формулу:
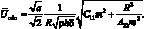 (4.85)
(4.85)
Однако, наибольший интерес представляют значения аргументов k и n, вблизи которых критическая скорость принимает минимальное значение.
Рассмотрим случай, при котором имеет место симметрическая форма потери устойчивости (n = 0) и критическая скорость принимает минимальное значение при 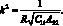 В этом случае для скорости получим:
В этом случае для скорости получим:
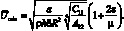 (4.86)
(4.86)
Для большей наглядности представим зависимость критической скорости от угла φ графически. Для этого преобразуем выражение (4.86) с учётом (4.84) и (4.74), (4.76), считая ε = 0
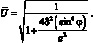 (4.87)
(4.87)
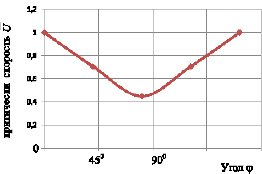
Рис. 4.11. Зависимость критической скорости от угла φ
Результат расчета приведен на рис. 4.11. Как видно из рисунка критическая скорость флаттера может меняться зависимости от угла φ
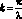 –
–