
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ РАДИОЛОКАЦИИ РАСПРЕДЕЛЁННЫХ ЦЕЛЕЙ
Применение сверхширокополосных сигналов и эффекта синтезирования апертуры за счёт движения Земли, перемещения космических, воздушных летательных аппаратов позволяет получить радиолокационное изображение (РЛИ) пространственно-распределённой цели (ПРЦ), характеризующееся достаточно высокой разрешающей способностью, при которой наблюдатель имеет возможность решать задачу классификации и распознавания названных ПРЦ.
Проблема классификации радиолокационных изображений ПРЦ, формируемых с помощью таких средств наблюдения, является частной задачей классической теории распознавания образов – ведущего научного направления современного естествознания, сложившегося и интенсивно развивающегося в течение последних десятилетий.
Фундаментальные основы статистической теории распознавания заложены в трудах Т. Андерсона [1], А.А. Харкевича [2], Г.С. Себастиана [3], М.М. Бонгарда [4] и др. Современное состояние этой теории подробно отражено в работах В.Н. Вапника и А.Я. Червоненкиса [5], Р. Дуды и П. Хафа [6], В.А. Ковалевского [7], Дж. Ту и Р. Гонсалеса [8], А.Л. Горелика [9, 10] и других авторов [11, 12].
Пространственно-распределенная цель представляет собой совокупность центров стабильного отражения («блестящих точек») и большого числа статистически однородных отражателей, равномерно распределенных по поверхности цели. В качестве модели последних может быть принята абсолютно шероховатая поверхность, отражения от которой образуют так называемую диффузионную составляющую сигнала.
Количество, положение и ЭПР центров стабильного отражения остаются практически постоянными при изменении ракурса цели на несколько градусов.
Примерами пространственно-распределённых целей могут служить радиолокационные изображения надводных кораблей, полученных космической РЛС с синтезированной апертурой.
На рис. 1.1 представлены РЛИ надводных кораблей для различных условий наблюдения [13, 14] при разрешающей способности РСА – верхний ряд – 15 м и нижний ряд – 35 м; ракурсе наблюдения 283° (А – В), 315° (Г – Е) и 270° (Ж – И); отсутствии качки (А, Г, Ж) и наличии боковой качки 10° на сторону (Б и Д) и 15° на сторону (В и Е), а также при совместном воздействии килевой качки и рысканья ±7° (З, И), где R – это направление по дальности, Х – направление по азимуту.
Формулировка существа проблемы заключается в том, чтобы, располагая исходным множеством объектов классификации и заданным априори принципом разделения этого множества на классы, распознающий автомат (РА) в соответствии с оптимальным или близким к нему алгоритмом сформировал из наблюдаемых данных вектор признаков L = {l1, .., lk} и в соответствии с эффективным решающим правилом разделил пространство признаков таким образом, чтобы, в лучшем случае, с максимальной, а в худшем случае, с заданной вероятностью определить класс очередного обнаруженного объекта. При этом общая постановка задачи классификации объектов радиолокационного наблюдения может быть сформулирована следующим образом.
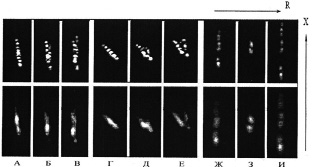
Рис. 1.1. Примеры РЛИ пространственно-распределенных целей (надводных кораблей)
Пусть задано множество B объектов различных типов. Система классификации состоит из P радиолокационных средств, содержащих РА. В каждом из таких РА используется множество радиолокационных сигналов S, на базе которых образуется множество признаков распознавания и множество правил принятия решения о классе наблюдаемого объекта K. Кроме того, введем множество параметров х, связанных с объектом и условиями его наблюдения, причем часть названных параметров х могут быть измерены РА, а часть параметров x0 не измеряются в процессе решения задачи классификации, но существенным образом влияют на ее эффективность, которая оценивается с помощью некоторого критерия Э{•}.
Если стоимость создания системы классификации С, а общие ассигнования – C0, то формально решение задачи сводится к отысканию экстремума функционала:
Э{P, S, L, K, x/B} (1.1)
при ограничении
C ≤ C0. (1.2)
Точные методы решения этой задачи неизвестны, что, вообще говоря, достаточно естественно в связи с чрезвычайно общим характером ее постановки. Разумной альтернативой может служить переход к более частной конкретной задаче с учетом реальных условий, связанных с особенностями решаемой проблемы. При рассматриваемой в работе классификации ПРЦ следует учесть некоторые ограничения, а именно, выраженный статистический характер проблемы, связанный с природой наблюдаемых данных и практической невозможностью решения электродинамической задачи, определяет целесообразность использования вероятностных признаков, отказываясь от детерминированного, логического и структурного подходов [15].
Указанные ограничения определяют методологию подхода к решению задачи классификации ПРЦ. При использовании любого из известных статистических критериев вектор оптимальных признаков L должен быть образован на основе коэффициентов правдоподобия Δ1, ΔM (где М – число классов) – достаточных статистик, а разбиение пространства решения на области, соответствующие каждому из классов, производится гиперплоскостями (причем, коэффициентами в уравнениях таких плоскостей служат в общем случае элементы матрицы стоимостей).
При полной априорной определенности о распознаваемых классах и условиях наблюдения, а также отсутствии технических ограничений на этом проблема была бы исчерпана. Однако при практическом использовании РА оба названных требования далеки от реальности. В первую очередь это связано с наличием множества мешающих параметров χ, которое делится на два подмножества: х – подмножество принципиально не измеряемых параметров и x0 – подмножество параметров, оцениваемых по наблюдаемым данным.
Если U(t) – вектор-функция наблюдаемых данных, то эффективные признаки следует искать, отталкиваясь от коэффициентов правдоподобия:
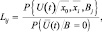 (1.3)
(1.3)
где P{•} – условный функционал плотности вероятности для реализации U(t); x0 – вектор оценок измеряемых параметров; xi – i-я комбинация
неизвестных параметров; Bj – указание на наличие цели j-гo класса (при В = 0 цель отсутствует).
Следует заметить, что размерность вектора L становится чрезвычайно большой в связи с континуальным в общем случае характером вектора х. С другой стороны, при его формировании возникает ряд проблем алгоритмического и технического характера. И, наконец, существующая в современных условиях база данных о радиолокационных портретах (РП) ПРЦ обычно настолько мала, что не позволяет говорить о достаточно достоверных сведениях о подавляющем большинстве индивидуальных характеристик, конструктивных и геометрических особенностей ПРЦ. Последнее обстоятельство не позволяет получить вектор с составляющими компонентами типа (1.3) и использовать их для классификации.
В связи с этим применяется следующая методология отыскания признаков. Названный вектор ищется на основе выражений для достаточных статистик в предположении о том, что РП и условия наблюдения заданы. После отыскания этих признаков они последовательно модифицируются с тем, чтобы полностью учесть имеющуюся априорную информацию с одновременным отказом от учета тех структурных и алгоритмических особенностей, которые недоступны на этапах проектирования и начальной боевой эксплуатации РА. В тоже время полученные алгоритмы не исключают, а напротив, предусматривают адаптацию к новым данным о РП и условиям наблюдения, полученным при опытной и боевой эксплуатации систем МКРЦ. Аналогичный подход реализуется и по отношению к решающим правилам.
Ряд конкретных решений задачи классификации ПРЦ приведён в работах [16–19].
